Tìm GTNN của hàm số y = \(\tan^2x\) - \(4\tan x\) + 1

Những câu hỏi liên quan
Tìm đạo hàm của các hàm số sau:1, y3^{(dfrac{x}{ln(x)})}2, ydfrac{1}{2}tan^2(x)+ln(tan(x))3, ysqrt[3]{ln^2(2x)}
Đọc tiếp
Tìm đạo hàm của các hàm số sau:
1, \(y=3^{(\dfrac{x}{\ln(x)})}\)
2, \(y=\dfrac{1}{2}tan^2(x)+\ln(tan(x))\)
3, \(y=\sqrt[3]{ln^2(2x)}\)
1.
\(y'=\left(\dfrac{x}{lnx}\right)'.3^{\dfrac{x}{lnx}}.ln3=\dfrac{lnx-1}{ln^2x}.3^{\dfrac{x}{lnx}}.ln3\)
2.
\(y'=\left(tanx\right)'.tanx+\left(tanx\right)'.\dfrac{1}{tanx}=\dfrac{tanx}{cos^2x}+\dfrac{1}{tanx.cos^2x}\)
3.
\(y=\left(ln2x\right)^{\dfrac{2}{3}}\Rightarrow y'=\left(ln2x\right)'.\dfrac{2}{3}.\left(ln2x\right)^{-\dfrac{1}{3}}=\dfrac{1}{3x\sqrt[3]{ln2x}}\)
Đúng 1
Bình luận (2)
Tìm đạo hàm của mỗi hàm số sau:
a) \(y = 4{x^3} - 3{x^2} + 2x + 10\)
b) \(y = \frac{{x + 1}}{{x - 1}}\)
c) \(y = - 2x\sqrt x \)
d) \(y = 3\sin x + 4\cos x - \tan x\)
e) \(y = {4^x} + 2{e^x}\)
f) \(y = x\ln x\)
a: \(y'=4\cdot3x^2-3\cdot2x+2=12x^2-6x+2\)
b: \(y'=\dfrac{\left(x+1\right)'\left(x-1\right)-\left(x+1\right)\left(x-1\right)'}{\left(x-1\right)^2}=\dfrac{x-1-x-1}{\left(x-1\right)^2}=\dfrac{-2}{\left(x-1\right)^2}\)
c: \(y'=-2\cdot\left(\sqrt{x}\cdot x\right)'\)
\(=-2\cdot\left(\dfrac{x+x}{2\sqrt{x}}\right)=-2\cdot\dfrac{2x}{2\sqrt{x}}=-2\sqrt{x}\)
d: \(y'=\left(3sinx+4cosx-tanx\right)\)'
\(=3cosx-4sinx+\dfrac{1}{cos^2x}\)
e: \(y'=\left(4^x+2e^x\right)'\)
\(=4^x\cdot ln4+2\cdot e^x\)
f: \(y'=\left(x\cdot lnx\right)'=lnx+1\)
Đúng 1
Bình luận (0)
tìm tập xác định của hàm số lượng giác saua)ydfrac{tanleft(2x-dfrac{pi}{4}right)}{sqrt{1-sinleft(x-dfrac{pi}{8}right)}}b)ydfrac{tanleft(x-dfrac{pi}{4}right)}{1-cosleft(x+dfrac{pi}{3}right)}c)ydfrac{3}{cosx-cos3x}d)ydfrac{4}{sin^2x-cos^2x}e)ydfrac{1+cotleft(dfrac{pi}{3}+xright)}{tan^2left(3x-dfrac{pi}{4}right)}
Đọc tiếp
tìm tập xác định của hàm số lượng giác sau
a)\(y=\dfrac{tan\left(2x-\dfrac{\pi}{4}\right)}{\sqrt{1-sin\left(x-\dfrac{\pi}{8}\right)}}\)
b)\(y=\dfrac{tan\left(x-\dfrac{\pi}{4}\right)}{1-cos\left(x+\dfrac{\pi}{3}\right)}\)
c)\(y=\dfrac{3}{cosx-cos3x}\)
d)\(y=\dfrac{4}{sin^2x-cos^2x}\)
e)\(y=\dfrac{1+cot\left(\dfrac{\pi}{3}+x\right)}{tan^2\left(3x-\dfrac{\pi}{4}\right)}\)
Với giá trị nào của x thì giá trị của các hàm số y = tan(π/4 - x) và y = tan 2x bằng nhau?
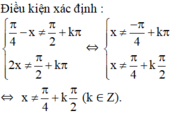
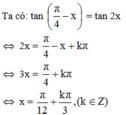
Kết hợp với điều kiện xác định suy ra
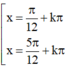 (k ∈ Z)
(k ∈ Z)
Vậy với 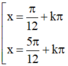 (k ∈ Z)
(k ∈ Z)
thì 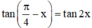
Đúng 0
Bình luận (0)
Tìm đạo hàm các hàm số:
1, \(y=\tan(3x-\dfrac{\pi}{4})+\cot(2x-\dfrac{\pi}{3})+\cos(x+\dfrac{\pi}{6})\)
2, \(y=\dfrac{\sqrt{\sin x+2}}{2x+1}\)
3, \(y=\cos(3x+\dfrac{\pi}{3})-\sin(2x+\dfrac{\pi}{6})+\cot(x+\dfrac{\pi}{4})\)
a.
\(y'=\dfrac{3}{cos^2\left(3x-\dfrac{\pi}{4}\right)}-\dfrac{2}{sin^2\left(2x-\dfrac{\pi}{3}\right)}-sin\left(x+\dfrac{\pi}{6}\right)\)
b.
\(y'=\dfrac{\dfrac{\left(2x+1\right)cosx}{2\sqrt{sinx+2}}-2\sqrt{sinx+2}}{\left(2x+1\right)^2}=\dfrac{\left(2x+1\right)cosx-4\left(sinx+2\right)}{\left(2x+1\right)^2}\)
c.
\(y'=-3sin\left(3x+\dfrac{\pi}{3}\right)-2cos\left(2x+\dfrac{\pi}{6}\right)-\dfrac{1}{sin^2\left(x+\dfrac{\pi}{4}\right)}\)
Đúng 2
Bình luận (0)
Tính đạo hàm của các hàm số sau:
a) y=\(\dfrac{3x^2-18x-2}{1-2x}-\dfrac{2x-3}{x+4}\)
b) y=\(-\dfrac{\sin x}{3\cos^3x}+\dfrac{4}{3}\tan x\)
Tìm GTLN (max); GTNN (min) của hàm số
y
2
x
+
1
+
4
-
x
.
Đọc tiếp
Tìm GTLN (max); GTNN (min) của hàm số y = 2 x + 1 + 4 - x .
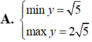
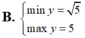
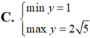
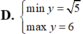
Tìm GTNN của hàm số \(Y=\dfrac{x^2+2x+33}{4x-4}\) với x>1
\(y=\dfrac{x+3}{4}+\dfrac{9}{x-1}=\dfrac{x-1}{4}+\dfrac{9}{x-1}+1\)
\(y\ge2\sqrt{\dfrac{9\left(x-1\right)}{4\left(x-1\right)}}+1=4\)
\(y_{min}=4\) khi \(x=7\)
Đúng 2
Bình luận (0)
Tính đạo hàm cấp hai của các hàm số sau:
a) \(y = \ln \left( {x + 1} \right);\)
b) \(y = \tan 2x.\)
a: y=ln(x+1)
=>\(y'=\dfrac{1}{x+1}\)
=>\(y''=\dfrac{1'\left(x+1\right)-1\left(x+1\right)'}{\left(x+1\right)^2}=\dfrac{-1}{\left(x+1\right)^2}\)
b: y=tan 2x
=>\(y'=\dfrac{2}{cos^22x}\)
=>\(y''=\left(\dfrac{2}{cos^22x}\right)'=\dfrac{-2\cdot cos^22x'}{cos^42x}=\dfrac{-2\cdot2\cdot cos2x\left(cos2x\right)'}{cos^42x}\)
\(=\dfrac{4\cdot2\cdot sin2x}{cos^32x}=\dfrac{8\cdot sin2x}{cos^32x}\)
Đúng 0
Bình luận (0)












