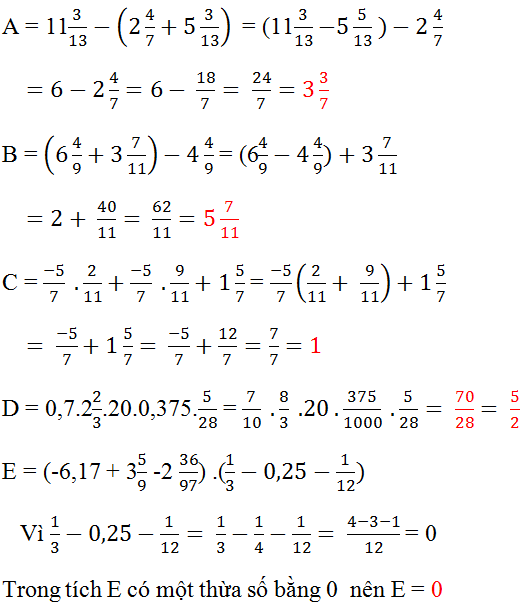Ta có: \(A=\dfrac{1+\dfrac{1}{3}+\dfrac{1}{5}+\dfrac{1}{7}+...+\dfrac{1}{97}+\dfrac{1}{99}}{\dfrac{1}{1\cdot99}+\dfrac{1}{3\cdot97}+\dfrac{1}{5\cdot95}+...+\dfrac{1}{97\cdot3}+\dfrac{1}{99\cdot1}}\)
\(\Leftrightarrow\dfrac{A}{100}=\dfrac{1+\dfrac{1}{3}+\dfrac{1}{5}+\dfrac{1}{7}+...+\dfrac{1}{97}+\dfrac{1}{99}}{\dfrac{100}{1\cdot99}+\dfrac{100}{3\cdot97}+\dfrac{100}{5\cdot95}+...+\dfrac{100}{97\cdot3}+\dfrac{100}{99\cdot1}}\)

\(\Leftrightarrow\dfrac{A}{100}=\dfrac{1+\dfrac{1}{3}+\dfrac{1}{5}+\dfrac{1}{7}+...+\dfrac{1}{97}+\dfrac{1}{99}}{1+\dfrac{1}{99}+\dfrac{1}{3}+\dfrac{1}{97}+\dfrac{1}{5}+\dfrac{1}{95}+...+\dfrac{1}{97}+\dfrac{1}{3}+\dfrac{1}{99}+1}\)

\(\Leftrightarrow\dfrac{A}{100}=\dfrac{1+\dfrac{1}{3}+\dfrac{1}{5}+\dfrac{1}{7}+...+\dfrac{1}{97}+\dfrac{1}{99}}{2\left(1+\dfrac{1}{3}+\dfrac{1}{5}+\dfrac{1}{7}+...+\dfrac{1}{97}+\dfrac{1}{99}\right)}\)

\(\Leftrightarrow\dfrac{A}{100}=\dfrac{1}{2}\)

hay A=50

A = \(\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\) . \(\left(\dfrac{1}{3}-0,25-\dfrac{1}{12}\right)\)

A = \(\left(-6,17+\dfrac{32}{9}-\dfrac{230}{97}\right)\) . \(\left(\dfrac{1}{3}-\dfrac{1}{4}-\dfrac{1}{12}\right)\)

A = \(\left(-6,17+\dfrac{32}{9}-\dfrac{230}{97}\right)\) . \(\left(\dfrac{4}{12}-\dfrac{3}{12}-\dfrac{1}{12}\right)\)

A = \(\left(-6,17+\dfrac{32}{9}-\dfrac{230}{97}\right)\) . 0

A = 0*

*Vì số nào nhân với 0 cũng bằng 0 nên không cần tính kết quả của phép tính\(\left(-6,17+\dfrac{32}{9}-\dfrac{230}{97}\right)\)

A = \(\dfrac{1}{\sqrt{3}+\sqrt{5}}+\dfrac{1}{\sqrt{5}+\sqrt{7}}+\dfrac{1}{\sqrt{7}+\sqrt{9}}+...+\dfrac{1}{\sqrt{97}+\sqrt{99}}\)

= \(\dfrac{1}{2}\left(\sqrt{5}-\sqrt{3}+\sqrt{7}-\sqrt{5}+\sqrt{9}-\sqrt{7}+...+\sqrt{99}-\sqrt{97}\right)\)

= \(\dfrac{1}{2}\left(\sqrt{99}-\sqrt{3}\right)\)

B = 35 + 335 + 3335 + ... + 3333...(99 số 3)35

= 33 + 2 + 333 + 2 + 3333 + 2 + ... + 333...33 + 2

= 2 . 99 + (33 + 333 + 3333 + ... + 333...3)

= 198 + \(\dfrac{1}{3}\)(99 + 999 + 9999 + ... + 999...99)

= 198 + \(\dfrac{1}{3}\)(10² - 1 + 10³ - 1 + 10⁴ - 1 + ... + 10¹⁰⁰ - 1)

= \(\left(\dfrac{10^{101}-10^2}{27}\right)+165\)

Nhận xét 1: từng hạng tử của A có dạng:

\(\dfrac{1}{\sqrt{x}+\sqrt{x+2}}\left(x\ge3\right)\)

Nhận xét 2:

\(\left(\sqrt{x+2}-\sqrt{x}\right)\left(\sqrt{x}+\sqrt{x+2}\right)=\left(x+2\right)-x=2\)

\(\Rightarrow\dfrac{2}{\sqrt{x}+\sqrt[]{x+2}}=-\sqrt{x}+\sqrt{x+2}\)

Áp dụng vào A:

\(2A=\dfrac{2}{\sqrt{3}+\sqrt{5}}+\dfrac{2}{\sqrt{5}+\sqrt{7}}+...+\dfrac{2}{\sqrt{97}+\sqrt{99}}\)

\(=\left(-\sqrt{3}+\sqrt{5}\right)+\left(-\sqrt{5}+\sqrt{7}\right)+...+\left(-\sqrt{97}+\sqrt{99}\right)\)

\(=-\sqrt{3}+\sqrt{99}\Leftrightarrow A=-2\sqrt{3}+2\sqrt{99}\)

A = \(\dfrac{1}{\sqrt{3}+\sqrt{5}}+\dfrac{1}{\sqrt{5}+\sqrt{7}}+\dfrac{1}{\sqrt{7}+\sqrt{9}}+...+\dfrac{1}{\sqrt{97}+\sqrt{99}}\)

=

\(\dfrac{\sqrt{5}-\sqrt{3}}{\left(\sqrt{3}+\sqrt{5}\right)\cdot\left(\sqrt{5}-\sqrt{3}\right)}+\dfrac{\sqrt{7}-\sqrt{5}}{\left(\sqrt{5}+\sqrt{7}\right)\cdot\left(\sqrt{7}-\sqrt{5}\right)}+\dfrac{\sqrt{9}-\sqrt{7}}{\left(\sqrt{7}+\sqrt{9}\right)\cdot\left(\sqrt{9}-\sqrt{7}\right)}+...+\dfrac{\sqrt{99}-\sqrt{97}}{\left(\sqrt{97}+\sqrt{99}\right)\cdot\left(\sqrt{99}-\sqrt{97}\right)}\)

= \(\dfrac{\sqrt{5}-\sqrt{3}}{5-3}+\dfrac{\sqrt{7}-\sqrt{5}}{7-5}+\dfrac{\sqrt{9}-\sqrt{7}}{9-7}+...+\dfrac{\sqrt{99}-\sqrt{97}}{99-97}\)

=\(\dfrac{\sqrt{5}-\sqrt{3}}{2}+\dfrac{\sqrt{7}-\sqrt{5}}{2}+\dfrac{\sqrt{9}-\sqrt{7}}{2}+...+\dfrac{\sqrt{99}-\sqrt{97}}{2}\)

=\(\dfrac{1}{2}\cdot\left(\sqrt{5}-\sqrt{3}+\sqrt{7}-\sqrt{5}+\sqrt{9}-\sqrt{7}+...+\sqrt{99}-\sqrt{97}\right)\)

= \(\dfrac{1}{2}\cdot\left(-\sqrt{3}+\sqrt{99}\right)\)

= \(\dfrac{3\sqrt{11}-\sqrt{3}}{2}\)

đó là ý kiến của mik còn đúng hay sai là tùy bn

\(A=11\dfrac{3}{13}-\left(2\dfrac{4}{7}+5\dfrac{3}{13}\right)\)

\(A=11\dfrac{3}{13}-5\dfrac{3}{13}-2\dfrac{4}{7}\)

\(A=6-2\dfrac{4}{7}\)

\(A=5\dfrac{7}{7}-2\dfrac{4}{7}\)

\(A=3\dfrac{3}{7}\)

\(B=\left(6\dfrac{4}{9}+3\dfrac{7}{11}\right)-4\dfrac{4}{9}\)

\(B=\left(6\dfrac{4}{9}-4\dfrac{4}{9}\right)+3\dfrac{7}{11}\)

\(B=2+3\dfrac{7}{11}\)

\(B=5\dfrac{7}{11}\)

\(C=\dfrac{-5}{7}.\dfrac{2}{11}+\dfrac{-5}{7}-\dfrac{9}{11}+1\dfrac{5}{7}\)

\(C=\dfrac{-5}{7}.\left(\dfrac{2}{11}+1\right)-\dfrac{9}{11}+1\dfrac{5}{7}\)

\(C=\dfrac{-5}{7}.\dfrac{13}{11}-\dfrac{9}{11}+1\dfrac{5}{7}\)

\(C=\dfrac{-65}{77}-\dfrac{9}{11}+1\dfrac{5}{7}\)

\(C=\dfrac{4}{11}+1\dfrac{5}{7}\)

\(C=\dfrac{160}{11}\)

\(D=0,7.2\dfrac{2}{3}.20.0,375.\dfrac{5}{28}\)

\(D=\dfrac{7}{10}.\dfrac{8}{3}.20.\dfrac{375}{1000}.\dfrac{5}{28}\)

\(D=\dfrac{7}{28}=\dfrac{5}{2}\)

\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{3}-0,25-\dfrac{1}{12}\right)\)

\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{3}-\dfrac{1}{4}-\dfrac{1}{12}\right)\)

\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{12}-\dfrac{1}{12}\right)\)

\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right).0\)

\(\Rightarrow E=0\)

( 1 + \(\dfrac{2}{5}\)).( 1 + \(\dfrac{2}{7}\) ).( 1 + \(\dfrac{2}{9}\)).( 1 + \(\dfrac{2}{11}\)).....( 1 + \(\dfrac{2}{97}\)).( 1 + \(\dfrac{2}{99}\))

= \(\dfrac{7}{5}\).\(\dfrac{9}{7}\).\(\dfrac{11}{9}\).\(\dfrac{13}{11}\)...\(\dfrac{99}{97}\).\(\dfrac{101}{99}\)

= \(\dfrac{7.9.11.13...99.101}{5.7.9.11...97.99}\)

= \(\dfrac{101}{5}\)

❤ HOK TT ❤

\(2\left(\dfrac{1}{\sqrt{1}+\sqrt{3}}+\dfrac{1}{\sqrt{5}+\sqrt{7}}+...+\dfrac{1}{\sqrt{97}+\sqrt{99}}\right)\)

\(>\dfrac{1}{\sqrt{1}+\sqrt{3}}+\dfrac{1}{\sqrt{3}+\sqrt{5}}+\dfrac{1}{\sqrt{5}+\sqrt{7}}+...+\dfrac{1}{\sqrt{97}+\sqrt{99}}+\dfrac{1}{\sqrt{99}+\sqrt{101}}\)

\(=\dfrac{1}{2}\left(\sqrt{3}-\sqrt{1}+\sqrt{5}-\sqrt{3}+...+\sqrt{101}-\sqrt{99}\right)\)

\(=\dfrac{1}{2}\left(\sqrt{101}-\sqrt{1}\right)>\dfrac{9}{2}\)

\(\Rightarrow\dfrac{1}{\sqrt{1}+\sqrt{3}}+\dfrac{1}{\sqrt{5}+\sqrt{7}}+...+\dfrac{1}{\sqrt{97}+\sqrt{99}}>\dfrac{9}{4}\)

\(\dfrac{1+\dfrac{1}{3}+\dfrac{1}{5}+\dfrac{1}{7} +.....................+\dfrac{1}{97}+\dfrac{1}{99}}{\dfrac{1}{1.99}+\dfrac{1}{3.97}+\dfrac{1}{5.95}+....+\dfrac{1}{97.3}+\dfrac{1}{99.1}}\)

\(=\dfrac{\left(1+\dfrac{1}{99}\right)+\left(\dfrac{1}{3}+\dfrac{1}{97}\right)+..........+\left(\dfrac{1}{49}+\dfrac{1}{51}\right)}{2\left(\dfrac{1}{1.99}+\dfrac{1}{3.97}+.......+\dfrac{1}{49.51}\right)}\)

\(=\dfrac{\dfrac{100}{1.99}+\dfrac{100}{3.97}+...........+\dfrac{100}{49.51}}{2\left(\dfrac{1}{1.99}+\dfrac{1}{3.97}+...........+\dfrac{1}{49.51}\right)}\)

\(=\dfrac{100\left(\dfrac{1}{1.99}+\dfrac{1}{3.97}+.............+\dfrac{1}{49.51}\right)}{2\left(\dfrac{1}{1.99}+\dfrac{1}{3.97}+..........+\dfrac{1}{49.51}\right)}\)

\(=\dfrac{100}{2}\)

\(=50\)

\(\dfrac{1+\dfrac{1}{3}+\dfrac{1}{5}+\dfrac{1}{7}+.....+\dfrac{1}{97}+\dfrac{1}{99}}{\dfrac{1}{1.99}+\dfrac{1}{3.97}+\dfrac{1}{5.95}+...+\dfrac{1}{97.3}+\dfrac{1}{99.1}}=\dfrac{\left(1+\dfrac{1}{99}\right)+\left(\dfrac{1}{3}+\dfrac{1}{97}\right)+....+\left(\dfrac{1}{49}+\dfrac{1}{51}\right)}{2\left(\dfrac{1}{1.99}+\dfrac{1}{3.97}+\dfrac{1}{5.95}+.....+\dfrac{1}{49.51}\right)}=\dfrac{\dfrac{100}{99}+\dfrac{100}{3.97}+....+\dfrac{100}{49.51}}{2\left(\dfrac{1}{1.99}+\dfrac{1}{3.97}+....+\dfrac{1}{49.51}\right)}=\dfrac{100}{2}=50\)