Tìm giá trị sau để phương trình sau có nghiệm
0,5(5x-1)=4,5-2m(x-2)
Bài 1:Tìm giá trị m để mỗi bất phương trình sau có nghiệm âm
a) 0,5(5x-1)=4,5-2m(x-2)
b) \(\dfrac{3mx+12m+5}{9m^2-1}\)=\(\dfrac{2x-3}{3m+1}\)-\(\dfrac{3x-4m}{1-3m}\)
a: =>2,5x-0,5-4,5+2m(x-2)
=>2,5x+2mx-4m-5=0
=>x(2m+2,5)=4m+5
=>x(4m+5)=8m+10
TH1: m=-5/4
=>Phương trình có vô số nghiệm
=>Nhận
TH2: m<>-5/4
Phương trình có nghiệm duy nhất là x=(8m+10)/(4m+5)=2(loại)
b: =>\(\dfrac{3mx+12m+5}{9m^2-1}=\dfrac{\left(2x-3\right)\left(3m-1\right)+\left(3x-4m\right)\left(3m+1\right)}{\left(3m-1\right)\left(3m+1\right)}\)
=>6xm-2x-9m+3+9xm+3x-12m^2-4m=3mx+12m+5
=>-12m^2+15xm+x-13m+3-3mx-12m-5=0
=>-12m^2+x(15m+1-3m)-25m-2=0
=>x(12m+1)=12m^2+25m+2
=>x(12m+1)=(m+2)(12m+1)
Th1: m=-1/12
=>PT luôn có nghiệm
=>Nhận
TH2: m<>-1/12
Để phương trình có nghiệm âm thì m+2<0
=>m<-2
Đối với mỗi phương trình sau, hãy tìm giá trị của m để phương trình có nghiệm, tính nghiệm của phương trình theo m: m x 2 + (2m – 1)x + m + 2 = 0
m x 2 + (2m – 1)x + m + 2 = 0 (1)
*Nếu m = 0, ta có (1) ⇔ -x + 2 = 0 ⇔ x = 2
*Nếu m ≠ 0 thì (1) có nghiệm khi và chỉ khi ∆ ≥ 0
Ta có : ∆ = 2 m - 1 2 – 4m(m + 2) = 4 m 2 – 4m + 1 – 4 m 2 – 8m
= -12m + 1
∆ ≥ 0 ⇔ -12m + 1 ≥ 0 ⇔ m ≤ 1/12
Vậy khi m ≤ 1/12 thì phương trình đã cho có nghiệm.
Giải phương trình (1) theo m :
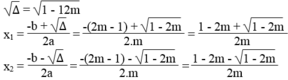
Bài 1: Tìm (P): y = ax2 + bx + c biết (P) có đỉnh I(2;1) và đi qua điểm A(4,5). Lập bảng biến thiên và vẽ (P).
Bài 2: Tìm tham số m để phương trình: (m2 - 1)x + 2m = 5x - 2√6 nghiệm đúng ∀x ∈ R
Bài 3: Cho phương trình: (2m - 1)x2 - 2(2m - 3)x + 2m + 5 = 0 (1)
Tìm m để phương trình:
a) Có nghiệm.
b) Có hai nghiệm phân biệt x1, x2 sao cho x1 = -x2.
Bài 4: Giải các phương trình sau:
![]()
Bài 5: Giải hệ phương trình sau: ![]()
Bài 6: Cho ΔABC có A(-1;1); B(1;3); C(1;-1)
a. ΔABC là tam giác gì? Tính chu vi và diện tích.
b. Tìm tọa độ tâm I và tính bán kính đường tròn ngoại tiếp tam giác ABC
c. Tìm tọa độ điểm D có hoành độ âm sao cho ΔADC vuông cân tại D.
tạo câu hỏi nhầm khối lớp rồi bạn=))
Đối với mỗi phương trình sau, hãy tìm giá trị của m để phương trình có nghiệm, tính nghiệm của phương trình theo m:
a. mx2 + (2m – 1)x + m + 2 = 0 b. 2x2 - (4m +3)x + 2m2 - 1 = 0
c. x2 – 2(m + 3)x + m2 + 3 = 0 d. (m + 1)x2 + 4mx + 4m +1 = 0
\(a.\Leftrightarrow mx^2+2mx-x+m+2=0\)
\(\Leftrightarrow mx\left(x+2\right)+\left(m+2\right)-x=0\)
\(\Leftrightarrow\left(m+2\right)\left(mx+1\right)-x=0\)
\(\Rightarrow\left\{{}\begin{matrix}m=\left(0+x\right):\left(mx+1\right)-2\\m=[\left(0+x\right):\left(m+2\right)-1]:x\end{matrix}\right.\)
Bài 1: Tìm m để các phương trình sau là phương trình bậc nhất một ẩn
a. (2m - 10). x +3 = 0
b. (m - 10). x +2019 = 0
Bài 2:
a. Tìm giá trị của b để phương trình 4x + 2b = 0 có nghiệm là x = 5
b. Tìm giá trị của b để phương trình 7x + b = 0 có nghiệm là x = 2
Các bạn giúp mk với ạ
Tìm các giá trị của m để bất phương trình sau vô nghiệm:
f(x) = (m + 1) x 2 - 2(3 - 2m)x + m + 1 ≥ 0
f(x) = (m + 1) x 2 - 2(3 - 2m)x + m + 1 ≥ 0 (1)
Với m = -1:
(1) ⇔ -10x ≥ 0 ⇔ x ≤ 0
Vậy với m = -1 bất phương trình (1) có nghiệm x ≤ 0
Suy ra, m = -1 (loại)
Với m ≠ -1:
f(x) = (m +1 ) x 2 - 2(3 - 2m)x + m + 1
Δ' = [-(3 - 2m) ] 2 - (m + 1)(m + 1) = (2m - 3 ) 2 - (m + 1 ) 2
= (2m - 3 + m + 1)(2m - 3 - m - 1) = (3m - 2)(m - 4)
Để bất phương trình (1) vô nghiệm thì:
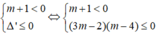
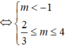
Vậy không có giá trị nào của m để bất phương trình (1) vô nghiệm
Cho phương trình 5x-( m+2) 5x+2m-1 = 0 với m là tham số thực. Có bao nhiêu giá trị nguyên để phương trình có nghiệm?
A. 2015
B. 2016
C. 2018
D. 2017
Chọn B.
Đặt t= 5x> 0.
+ Phương trình đã cho trở thành: t2-( m+2) t+2m-1=0 suy ra 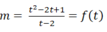 ( 2)
( 2)
( với t= 2 phương trình vô nghiệm).
Do đó phương trình đã cho có nghiệm khi phương trình (2) có nghiệm t> 0 .
+ Lập bảng biến thiên của hàm số f(t) dựa vào bảng biến thiên suy ra m ≤ 0 m ≥ 4
kết hợp điều kiện m nguyên và m ∈ [0;2018] => m ∈ {0;4;5;6;...;2018}
Vậy nghiệm 2016 giá trị của m thỏa mãn yêu cầu bài toán ra
Cho phương trình (2m−5)x2 −2(m−1)x+3=0 (1); với m là tham số thực
1) Tìm m để phương trình (1) có một nghiệm bằng 2, tìm nghiệm còn lại.
3) Tìm giá trị của m để phương trình đã cho có nghiệm
4) Xác định các giá trị nguyên của để phương trình đã cho có hai nghiệm phân biệt đều nguyên dương
1) điều kiện của m: m khác 5/2
thế x=2 vào pt1 ta đc:
(2m-5)*4 - 4(m-1)+3=0 <=> 8m-20-4m+4+3=0<=> 4m = 13 <=> m=13/4 (nhận)
lập △'=[-(m-1)]2-*(2m-5)*3 = (m-4)2
vì (m-4)2 ≥ 0 nên phương trình có nghiệm kép => x1= x2 =2
3) vì △'≥0 với mọi m nên phương trình đã cho có nghiệm với mọi m
Tìm giá trị của tham số m để phương trình sau vô nghiệm:\(\dfrac{x^2}{4}+\left(2m+1\right)x+5m^2+3m+16=0\)
Pt vô nghiệm khi:
\(\Delta=\left(2m+1\right)^2-\left(5m^2+3m+16\right)< 0\)
\(\Leftrightarrow-m^2+m-15< 0\) (luôn đúng)
Vậy pt đã cho vô nghiệm với mọi m