1. c

2. b

3. d

4. c

5. a

6. b

7. c

8. a

9. d

10. b

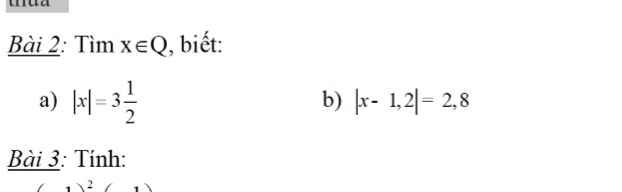
a) \(\left|x\right|=3\dfrac{1}{2}\)

\(\Rightarrow\left|x\right|=\dfrac{7}{2}\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=-\dfrac{7}{2}\end{matrix}\right.\)

b) \(\left|x-1,2\right|=2,8\)

\(\Rightarrow\left[{}\begin{matrix}x-1,2=2,8\\x-1,2=-2,8\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-1,6\end{matrix}\right.\)

\(a,\left|x\right|=3\dfrac{1}{2}\)

\(\Rightarrow x=\left[{}\begin{matrix}3\dfrac{1}{2}\\-3\dfrac{1}{2}\end{matrix}\right.\)

\(b,\left|x-1,2\right|=2,8\\ \Rightarrow\left[{}\begin{matrix}x-1,2=2,8\\x-1,2=-2,8\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=2,8+1,2=4\\x=-2,8+1,2=-1,6\end{matrix}\right.\)

Vậy \(x\in\left\{4;-1,6\right\}\)

Gọi số người mua là x(người), doanh thu là y(đồng)

(Điều kiện: \(x\in Z^+;y>0\))

Vì doanh thu bằng số người mua nhân với lại giá của bộ quần áo nên y=320000x(đồng)

=>\(320000=\dfrac{y}{x}\)

Số người mua tăng lên 60% và doanh thu cũng tăng thêm 30% nên giá mới sẽ là:

\(\dfrac{y\cdot\left(1+30\%\right)}{x\left(1+60\%\right)}=\dfrac{y}{x}\cdot\dfrac{13}{16}=320000\cdot\dfrac{13}{16}=260000\left(đồng\right)\)

\(9,PT\Leftrightarrow x-6=3x-7\left(x\ge6\right)\\ \Leftrightarrow x=\dfrac{1}{2}\left(ktm\right)\\ \Leftrightarrow x\in\varnothing\\ 10,PT\Leftrightarrow3x-2=4x^2-4x+1\left(x\le\dfrac{1}{2}\right)\\ \Leftrightarrow4x^2-7x+3=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{3}{4}\end{matrix}\right.\left(ktm\right)\Leftrightarrow x\in\varnothing\\ 11,PT\Leftrightarrow\sqrt{x^2+x-1}=2-x\left(x\le2\right)\\ \Leftrightarrow x^2+x-1=x^2-4x+4\\ \Leftrightarrow5x=5\Leftrightarrow x=1\left(tm\right)\\ 12,PT\Leftrightarrow\left(\sqrt{20-x}-4\right)+\left(\sqrt{x+5}-3\right)=0\left(5\le x\le20\right)\\ \Leftrightarrow\dfrac{4-x}{\sqrt{20-x}+4}+\dfrac{x-4}{\sqrt{x+5}+3}=0\\ \Leftrightarrow\left(x-4\right)\left(\dfrac{1}{\sqrt{x+5}+3}-\dfrac{1}{\sqrt{20-x}+4}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\\dfrac{1}{\sqrt{x+5}+3}=\dfrac{1}{\sqrt{20-x}+4}\left(1\right)\end{matrix}\right.\\ \left(1\right)\Leftrightarrow\sqrt{x+5}+3=\sqrt{20-x}+4\\ \Leftrightarrow\left(\sqrt{x+5}-4\right)-\left(\sqrt{20-x}-3\right)=0\\ \Leftrightarrow\dfrac{x-11}{\sqrt{x+5}+4}+\dfrac{x-11}{\sqrt{20-x}+3}=0\\ \Leftrightarrow\left(x-11\right)\left(\dfrac{1}{\sqrt{x+5}+4}+\dfrac{1}{\sqrt{20-x}+3}\right)=0\\ \Leftrightarrow x=11\left(\dfrac{1}{\sqrt{x+5}+4}+\dfrac{1}{\sqrt{20-x}+3}>0\right)\\ \text{Vậy PT có nghiệm }x\in\left\{4;11\right\}\)

\(13,PT\Leftrightarrow\sqrt{x-1}+\sqrt{3x-2}=\sqrt{5x+1}\left(x\ge-\dfrac{1}{5}\right)\\ \Leftrightarrow4x-3+2\sqrt{\left(x-1\right)\left(3x-2\right)}=5x+1\\ \Leftrightarrow x+4=2\sqrt{3x^2-5x+2}\\ \Leftrightarrow x^2+8x+16=12x^2-20x+8\\ \Leftrightarrow11x^2-28x-8=0\\ \Delta'=14^2+8\cdot11=284\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{14-2\sqrt{71}}{11}\\x=\dfrac{14+2\sqrt{71}}{11}\end{matrix}\right.\)

\(14,ĐK:x\ge-1\)

Đặt \(\sqrt{x+1}=a\ge0\)

\(PT\Leftrightarrow2\sqrt{a^2-1+2a}-a=4\\ \Leftrightarrow2\sqrt{a^2+2a-1}=a+4\\ \Leftrightarrow4a^2+8a-4=a^2+8a+16\\ \Leftrightarrow3a^2-20=0\\ \Leftrightarrow a^2=\dfrac{20}{3}\Leftrightarrow x+1=\dfrac{20}{3}\Leftrightarrow x=\dfrac{17}{3}\left(tm\right)\)

\(15,ĐK:-3\le x\le6\)

Đặt \(\sqrt{x+3}+\sqrt{6-x}=a\ge0\)

\(\Leftrightarrow\dfrac{a^2-9}{2}=\sqrt{\left(x+3\right)\left(6-x\right)}\\ PT\Leftrightarrow a-\dfrac{a^2-9}{2}=3\\ \Leftrightarrow2a-a^2+9=6\\ \Leftrightarrow a^2-2a-3=0\\ \Leftrightarrow a=3\left(a\ge0\right)\\ \Leftrightarrow\sqrt{x+3}+\sqrt{6-x}=3\\ \Leftrightarrow\sqrt{x+3}-3+\sqrt{6-x}=0\\ \Leftrightarrow\dfrac{x-6}{\sqrt{x+3}+3}-\dfrac{x-6}{\sqrt{6-x}}=0\\ \Leftrightarrow\left[{}\begin{matrix}x=6\left(tm\right)\\\dfrac{1}{\sqrt{x+3}+3}=\dfrac{1}{\sqrt{6-x}}\left(1\right)\end{matrix}\right.\\ \left(1\right)\Leftrightarrow\sqrt{x+3}+3=\sqrt{6-x}\\ \Leftrightarrow\sqrt{x+3}-\left(\sqrt{6-x}-3\right)=0\\ \Leftrightarrow\dfrac{x+3}{\sqrt{x+3}}+\dfrac{x+3}{\sqrt{6-x}+3}=0\\ \Leftrightarrow x=-3\left(\dfrac{1}{\sqrt{x+3}}+\dfrac{1}{\sqrt{6-x}+3}>0\right)\\ \text{Vậy PT có nghiệm }x\in\left\{6;-3\right\}\) 

\(16,\) Đặt \(\sqrt{x^2-6x+6}=a\ge0\)

\(PT\Leftrightarrow a^2+3=4a\\ \Leftrightarrow a^2-4a+3=0\\ \Leftrightarrow\left[{}\begin{matrix}a=1\\a=3\end{matrix}\right.\)

Với \(a=1\Leftrightarrow x^2-6x+5=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)

Với \(a=3\Leftrightarrow x^2-6x-3=0\Leftrightarrow\left[{}\begin{matrix}x=3+2\sqrt{3}\\x=3-2\sqrt{3}\end{matrix}\right.\)

Vậy PT có nghiệm \(x\in\left\{1;5;3+2\sqrt{3};3-2\sqrt{3}\right\}\)

a: ĐKXĐ x>0; x<>1

\(A=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}-1}{1}=\dfrac{x-1}{\sqrt{x}}\)

b: A<0

=>x-1<0

=>0<x<1

Bài 5 : 

a)

$2Na + 2HCl \to 2NaCl + H_2$
$Mg + 2HCl \to MgCl_2 + H_2$
$2Al + 6HCl \to 2AlCl_3 + 3H_2$
$Fe + 2HCl \to FeCl_2 + H_2$
$CuO + 2HCl \to CuCl_2 + H_2O$
$CaO + 2HCl \to CaCl_2 + H_2O$
$Fe(OH)_2 + 2HCl \to FeCl_2 + 2H_2O$
$NaOH + HCl \to NaCl + H_2O$

$Cu(OH)_2 + 2HCl \to CuCl_2 + 2H_2O$

$CaCO_3 + 2HCl \to CaCl_2 + CO_2 + H_2O$
$AgNO_3 + HCl \to AgCl + HNO_3$

$Na_2SO_3 + 2HCl \to 2NaCl + SO_2 + H_2O$

b)

$2Na + H_2SO_4 \to Na_2SO_4 + H_2$
$Mg + H_2SO_4 \to MgSO_4 + H_2$

$Fe + H_2SO_4 \to FeSO_4 + H_2
$2Al + 3H_2SO_4 \to Al_2(SO_4)_3 + 3H_2$
$CuO + H_2SO_4 \to CuSO_4 + H_2O$
$CaO + H_2SO_4 \to CaSO_4 + H_2O$
$Fe(OH)_2 + H_2SO_4 \to FeSO_4 + 2H_2O$
$2NaOH + H_2SO_4 \to Na_2SO_4 + 2H_2O$
$Cu(OH)_2 + H_2SO_4 \to CuSO_4 + 2H_2O$
$CaCO_3 + H_2SO_4 \to CaSO_4 + CO_2 + H_2O$
$Na_2SO_3 + H_2SO_4 \to Na_2SO_4 + SO_2 + H_2O$

$BaCl_2 + H_2SO_4 \to BaSO_4 + 2HCl$

Bài 5 :

\(Na+H_2O\rightarrow NaOH+\dfrac{1}{2}H_2\)

\(NaOH+HCl\rightarrow NaCl+H_2O\)

\(Mg+2HCl\rightarrow MgCl_2+H_2\)

\(2Al+6HCl\rightarrow2AlCl_3+3H_2\)

\(Fe+2HCl\rightarrow FeCl_2+H_2\)

\(CuO+2HCl\rightarrow CuCl_2+H_2O\)

\(CaO+H_2O\rightarrow Ca\left(OH\right)_2\)

\(Ca\left(OH\right)_2+2HCl\rightarrow CaCl_2+2H_2O\)

\(Fe\left(OH\right)_2+2HCl\rightarrow FeCl_2+H_2O\)

\(Cu\left(OH\right)_2+2HCl\rightarrow CuCl_2+H_2O\)

\(CaCO_3+2HCl\rightarrow CaCl_2+H_2O+CO_2\)

\(Na_2SO_3+2HCl\rightarrow2NaCl+H_2O+SO_2\)

\(AgNO_3+HCl\rightarrow AgCl+HNO_3\)

( Các chất không phản ứng với HCl là : Ag, BaCl2 )

- Với H2SO4 cũng tương tự như HCl nha chỉ cần thay vào thôi và thêm phản ứng :

\(BaCl_2+H_2SO_4\rightarrow BaSO_4+2HCl\)

Bài 5 : 

a)

$2Na + 2HCl \to 2NaCl + H_2$
$Mg + 2HCl \to MgCl_2 + H_2$
$2Al + 6HCl \to 2AlCl_3 + 3H_2$
$Fe + 2HCl \to FeCl_2 + H_2$
$CuO + 2HCl \to CuCl_2 + H_2O$
$CaO + 2HCl \to CaCl_2 + H_2O$
$Fe(OH)_2 + 2HCl \to FeCl_2 + 2H_2O$
$NaOH + HCl \to NaCl + H_2O$

$Cu(OH)_2 + 2HCl \to CuCl_2 + 2H_2O$

$CaCO_3 + 2HCl \to CaCl_2 + CO_2 + H_2O$
$AgNO_3 + HCl \to AgCl + HNO_3$

$Na_2SO_3 + 2HCl \to 2NaCl + SO_2 + H_2O$

b)

$2Na + H_2SO_4 \to Na_2SO_4 + H_2$
$Mg + H_2SO_4 \to MgSO_4 + H_2$

$Fe + H_2SO_4 \to FeSO_4 + H_2$
$2Al + 3H_2SO_4 \to Al_2(SO_4)_3 + 3H_2$
$CuO + H_2SO_4 \to CuSO_4 + H_2O$
$CaO + H_2SO_4 \to CaSO_4 + H_2O$
$Fe(OH)_2 + H_2SO_4 \to FeSO_4 + 2H_2O$
$2NaOH + H_2SO_4 \to Na_2SO_4 + 2H_2O$
$Cu(OH)_2 + H_2SO_4 \to CuSO_4 + 2H_2O$
$CaCO_3 + H_2SO_4 \to CaSO_4 + CO_2 + H_2O$
$Na_2SO_3 + H_2SO_4 \to Na_2SO_4 + SO_2 + H_2O$

$BaCl_2 + H_2SO_4 \to BaSO_4 + 2HCl$

5a.

Pt có 2 nghiệm pb lhi:

\(\Delta=9+4m>0\Leftrightarrow m>-\dfrac{9}{4}\)

b. Phương trình có 2 nghiệm khi:

\(\Delta=1+4\left(-2m+1\right)\ge0\Rightarrow m\le\dfrac{5}{8}\)

6.

a. Pt có 2 nghiệm khi: 

\(\Delta'=1-\left(m+2\right)\ge0\Leftrightarrow m\le-1\)

6b

Khi \(m\le-1\), theo hệ thức Viet ta có: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m+2\end{matrix}\right.\)

\(x^2_1+x^2_2=10\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=10\)

\(\Leftrightarrow4-2\left(m+2\right)=10\)

\(\Leftrightarrow m=-5\)

B.

\(x^2_1+x_2^2+4x_1x_2=0\)

\(\Leftrightarrow\left(x_1+x_2\right)^2+2x_1x_2=0\)

\(\Leftrightarrow4+2\left(m+2\right)=0\)

\(\Leftrightarrow m=-4\)

C.

Để biểu thức đề bài xác định \(\Rightarrow x_1x_2\ne0\Rightarrow m\ne-2\)

Khi đó:

\(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}=-3\Leftrightarrow\dfrac{x_1^2+x_2^2}{x_1x_2}=-3\)

\(\Rightarrow\left(x_1+x_2\right)^2-2x_1x_2=-3x_1x_2\)

\(\Leftrightarrow\left(x_1+x_2\right)^2+x_1x_2=0\)

\(\Leftrightarrow4+m+2=0\)

\(\Leftrightarrow m=-6\)

D.

\(x_1^3+x_2^3=15\Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=15\)

\(\Leftrightarrow8-6\left(m+2\right)=15\)

\(\Leftrightarrow m=-\dfrac{19}{6}\)