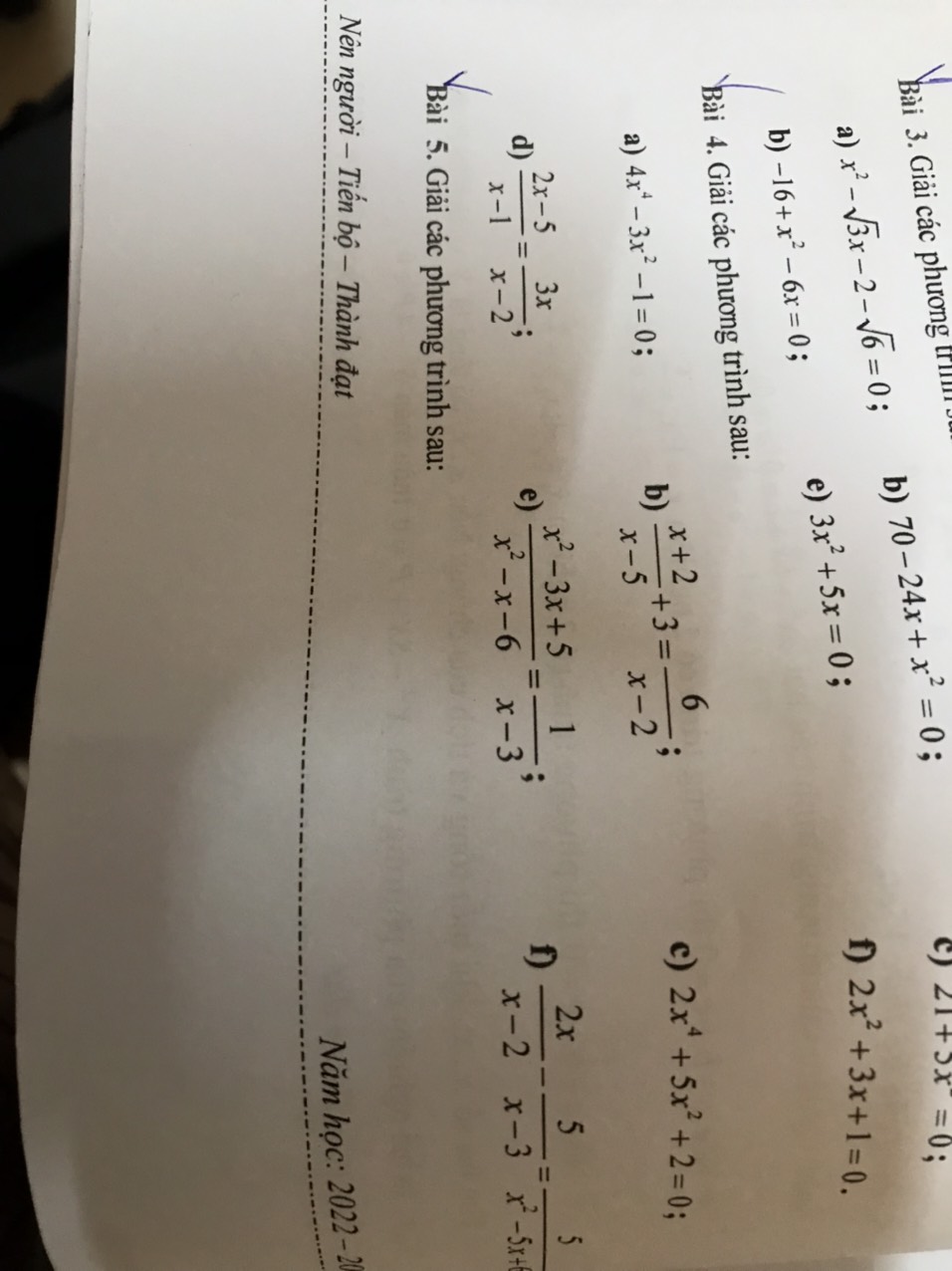5a.
Pt có 2 nghiệm pb lhi:
\(\Delta=9+4m>0\Leftrightarrow m>-\dfrac{9}{4}\)
b. Phương trình có 2 nghiệm khi:
\(\Delta=1+4\left(-2m+1\right)\ge0\Rightarrow m\le\dfrac{5}{8}\)
6.
a. Pt có 2 nghiệm khi:
\(\Delta'=1-\left(m+2\right)\ge0\Leftrightarrow m\le-1\)
6b
Khi \(m\le-1\), theo hệ thức Viet ta có: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m+2\end{matrix}\right.\)
\(x^2_1+x^2_2=10\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=10\)
\(\Leftrightarrow4-2\left(m+2\right)=10\)
\(\Leftrightarrow m=-5\)
B.
\(x^2_1+x_2^2+4x_1x_2=0\)
\(\Leftrightarrow\left(x_1+x_2\right)^2+2x_1x_2=0\)
\(\Leftrightarrow4+2\left(m+2\right)=0\)
\(\Leftrightarrow m=-4\)
C.
Để biểu thức đề bài xác định \(\Rightarrow x_1x_2\ne0\Rightarrow m\ne-2\)
Khi đó:
\(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}=-3\Leftrightarrow\dfrac{x_1^2+x_2^2}{x_1x_2}=-3\)
\(\Rightarrow\left(x_1+x_2\right)^2-2x_1x_2=-3x_1x_2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2+x_1x_2=0\)
\(\Leftrightarrow4+m+2=0\)
\(\Leftrightarrow m=-6\)
D.
\(x_1^3+x_2^3=15\Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=15\)
\(\Leftrightarrow8-6\left(m+2\right)=15\)
\(\Leftrightarrow m=-\dfrac{19}{6}\)
E.
\(2\left(x_1^2+x_2^2\right)-\left(x_1+x_2\right)^2=2x_1x_2-5\)
\(\Leftrightarrow2\left(x_1+x_2\right)^2-4x_1x_2-\left(x_1+x_2\right)^2-2x_1x_2+5=0\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-6x_1x_2+5=0\)
\(\Leftrightarrow4-6\left(m+2\right)+5=0\)
\(\Leftrightarrow m=-\dfrac{1}{2}\)
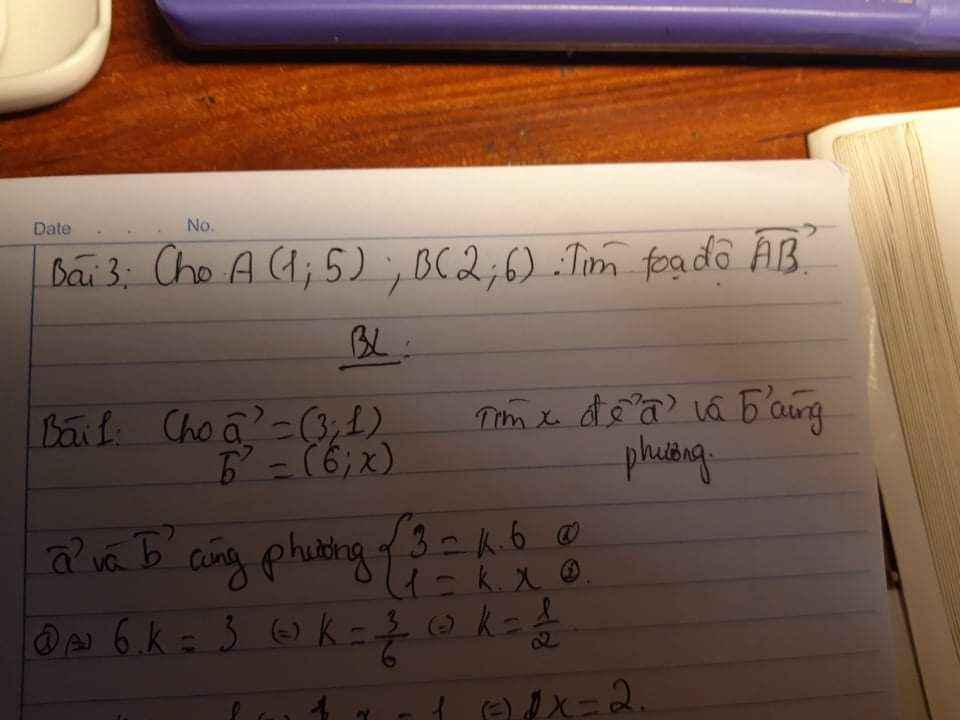
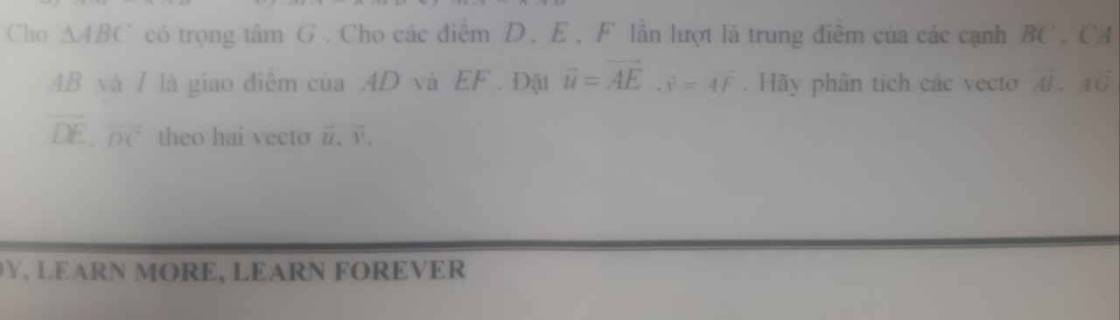
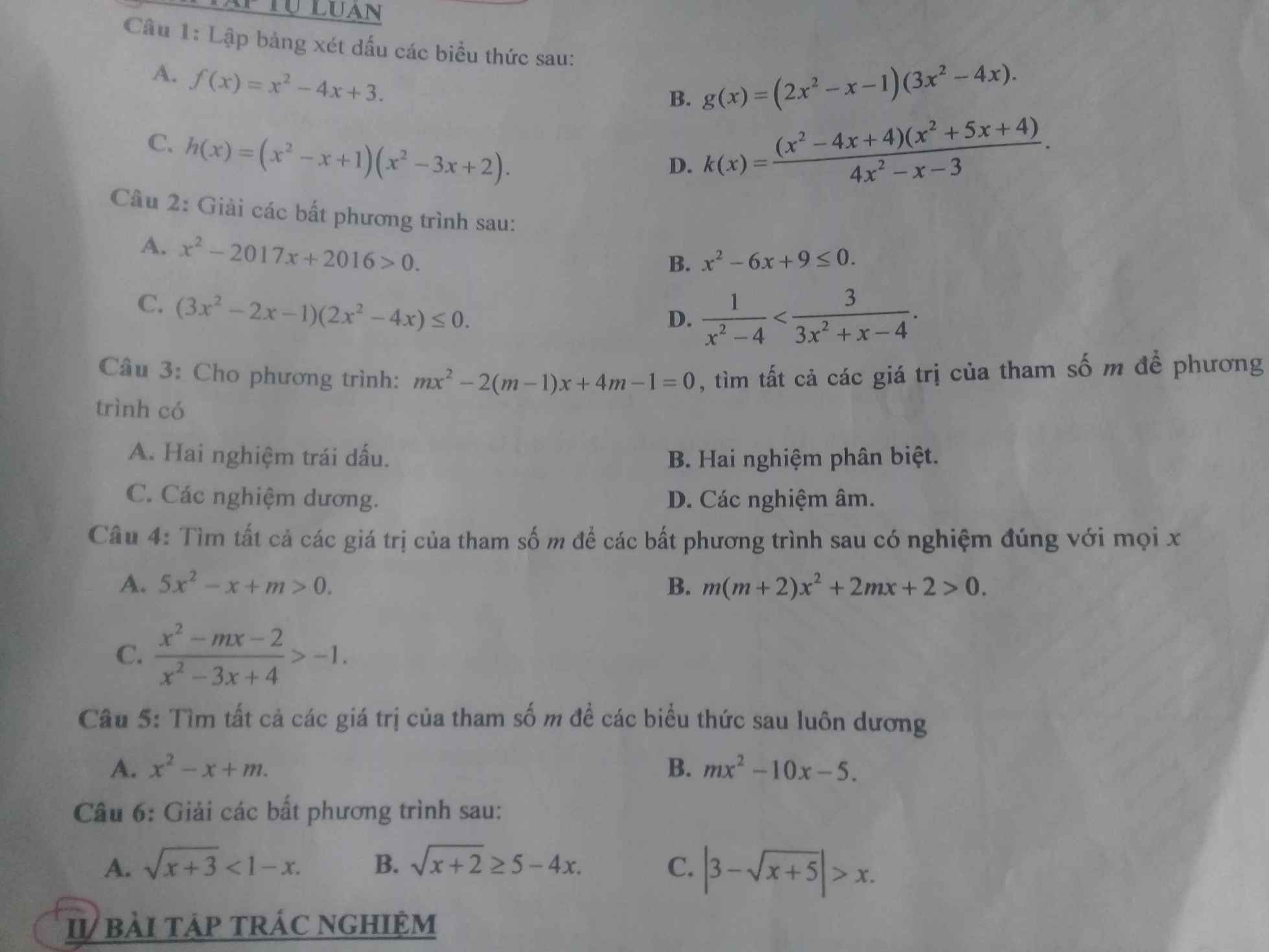
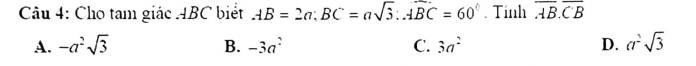
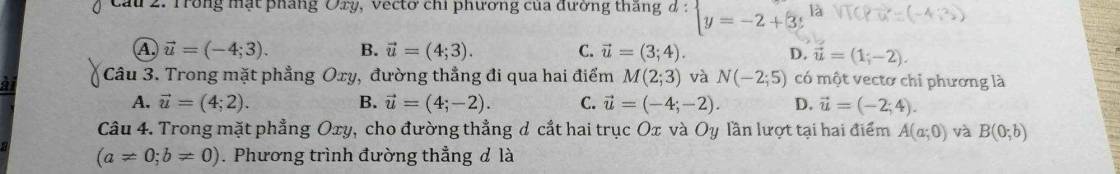giúp mình câu 3 với nha, giải ra luôn ạ 
