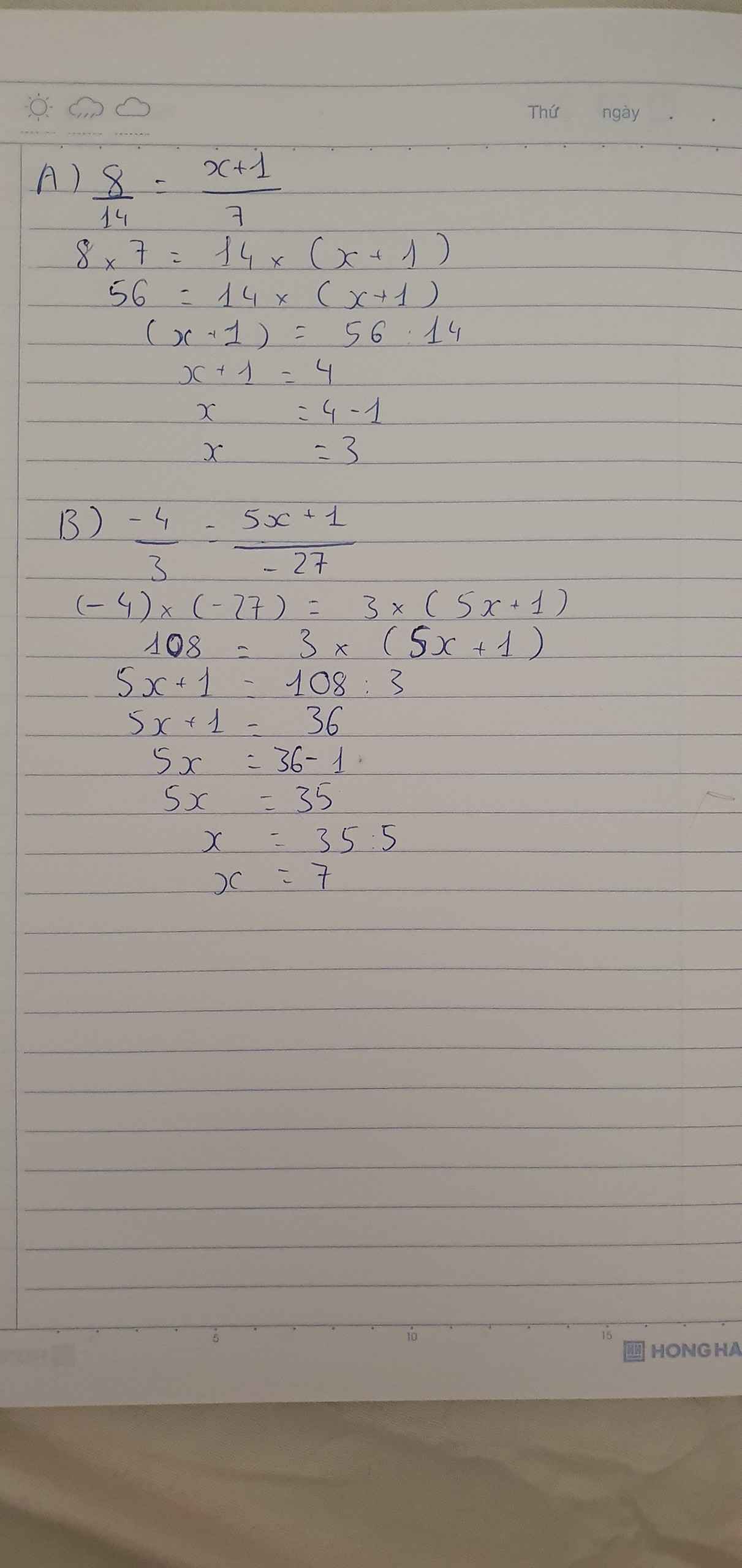Tìm x \(\dfrac{5x}{4}=\dfrac{80}{120}\)

Những câu hỏi liên quan
Tìm x, y biết
\(\dfrac{x}{y}=\dfrac{8}{5}\)và 5x+4y=120
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{5}=\dfrac{5x+4y}{5\cdot8+4\cdot5}=\dfrac{120}{60}=2\)
Do đó: x=16; y=10
Đúng 1
Bình luận (0)
1) sin2x + 2cosx = 0
2) sin(2x -10*) = \(\dfrac{1}{2}\) (-120* <x< 90*)
3) cos(2x+10*)= \(\dfrac{\sqrt{2}}{2}\)(-180*<x<180*)
4) \(\sin^2\left(5x+\dfrac{2\pi}{5}\right)-\cos^2\)(\(\dfrac{x}{4}-\pi\)) =0
1.
\(\Leftrightarrow2sinx.cosx+2cosx=0\)
\(\Leftrightarrow2cosx\left(sinx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sinx=-1\end{matrix}\right.\)
\(\Leftrightarrow cosx=0\) (do \(cosx=0\Leftrightarrow sinx=\pm1\) bao hàm luôn cả pt \(sinx=-1\))
\(\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\)
2.
\(\Leftrightarrow\left[{}\begin{matrix}2x-10^0=60^0+k360^0\\2x-10^0=120^0+n360^0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=35^0+k180^0\\x=65^0+n180^0\end{matrix}\right.\)
Do \(-120^0< x< 90^0\Rightarrow\left\{{}\begin{matrix}-120^0< 35^0+k180^0< 90^0\\-120^0< 65^0+n180^0< 90^0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}k=0\\n=\left\{-1;0\right\}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=35^0\\x=-115^0\\x=65^0\end{matrix}\right.\)
Đúng 1
Bình luận (2)
3. Làm tương tự câu 2
4.
\(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{2}cos\left(10x+\dfrac{4\pi}{5}\right)-\left(\dfrac{1}{2}+\dfrac{1}{2}cos\left(\dfrac{x}{2}-2\pi\right)\right)=0\)
\(\Leftrightarrow cos\left(10x+\dfrac{4\pi}{5}\right)+cos\left(\dfrac{x}{2}-2\pi\right)=0\)
\(\Leftrightarrow cos\left(10x+\dfrac{4\pi}{5}\right)+cos\left(\dfrac{x}{2}\right)=0\)
\(\Leftrightarrow cos\left(10x+\dfrac{4\pi}{5}\right)=-cos\left(\dfrac{x}{2}\right)=cos\left(\pi-\dfrac{x}{2}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}10x+\dfrac{4\pi}{5}=\pi-\dfrac{x}{2}+k2\pi\\10x+\dfrac{4\pi}{5}=\dfrac{x}{2}-\pi+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
Đúng 2
Bình luận (0)
Tìm x biết:
\(\dfrac{1}{120}\).120+x:\(\dfrac{1}{3}\)=\(-4\)
\(\dfrac{1}{120}\cdot120+x:\dfrac{1}{3}=-4\)
\(\Leftrightarrow1+x\cdot3=-4\)
\(\Leftrightarrow3x=-5\)
\(\Leftrightarrow x=-\dfrac{5}{3}\)
Đúng 3
Bình luận (0)
\(\dfrac{1}{120}.120+x:\dfrac{1}{3}=-4\)
\(1+x:\dfrac{1}{3}=-4\)
\(x:\dfrac{1}{3}=-4-1\)
\(x:\dfrac{1}{3}=-5\)
\(x=-5.\dfrac{1}{3}\)
\(x=\dfrac{-5}{3}\)
Đúng 0
Bình luận (0)
\(\left\{{}\begin{matrix}\dfrac{120}{x}=\dfrac{80}{y}\\\dfrac{96}{x}+1=\dfrac{104}{y}\end{matrix}\right.\) giải hệ
=>3/x=2/y và 96/x+1=104/y
=>2x=3y và 96/x+1=104/y
=>x/3=y/2=k và 96/x+1=104/y
=>x=3k; y=2k
\(\dfrac{96}{x}+1=\dfrac{104}{y}\)
=>\(\dfrac{96}{3k}+1=\dfrac{104}{2k}\)
=>\(\dfrac{32}{k}+1=\dfrac{52}{k}\)
=>20/k=1
=>k=20
=>x=60; y=40
Đúng 0
Bình luận (0)
Tìm x biết:
(\(\dfrac{1}{24.25}\)+\(\dfrac{1}{25.26}\)+...+\(\dfrac{1}{29.30}\)).120+x:\(\dfrac{1}{3}\)=\(-4\)
Lời giải:
\(\frac{1}{24.25}+\frac{1}{25.26}+...+\frac{1}{29.30}=\frac{25-24}{24.25}+\frac{26-25}{25.26}+...+\frac{30-29}{29.30}\)
\(=\frac{1}{24}-\frac{1}{25}+\frac{1}{25}-\frac{1}{26}+...+\frac{1}{29}-\frac{1}{30}\)
\(=\frac{1}{24}-\frac{1}{30}=\frac{1}{120}\)
Vậy:
\(\frac{1}{120}.120+x:\frac{1}{3}=-4\)
\(1+x:\frac{1}{3}=-4\)
\(x:\frac{1}{3}=-5\)
\(x=-15\)
Đúng 1
Bình luận (0)
\(\left(\dfrac{1}{24.25}+\dfrac{1}{25.26}+...+\dfrac{1}{29.30}\right).120+x:\dfrac{1}{3}=-4\)
\(\left(\dfrac{1}{24}-\dfrac{1}{25}+\dfrac{1}{25}-\dfrac{1}{26}+...+\dfrac{1}{29}-\dfrac{1}{30}\right).120+x:\dfrac{1}{3}=-4\)
\(\left(\dfrac{1}{24}-\dfrac{1}{30}\right).120+x:\dfrac{1}{3}=-4\)
\(\dfrac{1}{120}.120+x:\dfrac{1}{3}=-4\)
\(1+x:\dfrac{1}{3}=-4\)
\(x:\dfrac{1}{3}=-4-1\)
\(x:\dfrac{1}{3}=-5\)
\(x=-5.\dfrac{1}{3}\)
\(x=\dfrac{-5}{3}\)
Đúng 0
Bình luận (0)
a) 5(k+3x)(x+1)-4(1+2x)80 x_02Tìm gt của kb) x+1xc) x+20d) x+50e) (x+1)(2x-3)-3(x-2)2(x-1)^2f) (x+1)(x^2-x+1)-2xx(x-1)(x+1)g)dfrac{x}{3}-dfrac{5x}{6}-dfrac{15x}{12}dfrac{x}{4}-5h) dfrac{x-1}{2}-dfrac{x+1}{15}-dfrac{2x-13}{6}0i) dfrac{3left(5x-2right)}{4}-2dfrac{7x}{3}-5(x-7)j) dfrac{x-3}{11}+dfrac{x+1}{3}dfrac{x+7}{9}-1k)dfrac{3x-0,4}{2}+dfrac{1,5-2x}{3}dfrac{x+0,5}{5}l) dfrac{x-4}{5}+dfrac{3x-2}{10}-xdfrac{2x-5}{3}-dfrac{7x+2}{6}m) dfrac{left(2x-3right)left(2x+3right)}{8}dfrac{left(x-4right)...
Đọc tiếp
a) 5(k+3x)(x+1)-4(1+2x)=80 x\(_0\)=2Tìm gt của kb) x+1=xc) x+2=0d) x+5=0e) (x+1)(2x-3)-3(x-2)=2(x-1)\(^2\)f) (x+1)(x\(^2\)-x+1)-2x=x(x-1)(x+1)g)\(\dfrac{x}{3}\)-\(\dfrac{5x}{6}\)-\(\dfrac{15x}{12}\)=\(\dfrac{x}{4}\)-5h) \(\dfrac{x-1}{2}\)-\(\dfrac{x+1}{15}\)-\(\dfrac{2x-13}{6}\)=0i) \(\dfrac{3\left(5x-2\right)}{4}\)-2=\(\dfrac{7x}{3}\)-5(x-7)
j) \(\dfrac{x-3}{11}\)+\(\dfrac{x+1}{3}\)=\(\dfrac{x+7}{9}\)-1k)\(\dfrac{3x-0,4}{2}\)+\(\dfrac{1,5-2x}{3}\)=\(\dfrac{x+0,5}{5}\)l) \(\dfrac{x-4}{5}\)+\(\dfrac{3x-2}{10}\)-x=\(\dfrac{2x-5}{3}\)-\(\dfrac{7x+2}{6}\)m) \(\dfrac{\left(2x-3\right)\left(2x+3\right)}{8}\)=\(\dfrac{\left(x-4\right)^{^2}}{6}\)+\(\dfrac{\left(x-2^{ }\right)^2}{3}\)n) \(\dfrac{7x^2-14x-5}{15}\)=\(\dfrac{\left(2x+1\right)^2}{5}\)-\(\dfrac{\left(x-1\right)^2}{3}\)o) \(\dfrac{\left(7x+1\right)\left(x-2\right)}{10}\)+\(\dfrac{2}{5}\)=\(\dfrac{\left(x-2^{ }\right)^2}{5}\)+\(\dfrac{\left(x-1\right)\left(x-2\right)}{10}\)
Chia câu hỏi ra cho thành nhiều phần cho dễ trả lời á bạn
Đúng 2
Bình luận (1)
Cho đa thức \(P\left(x\right)=\dfrac{5x^3}{4}+\dfrac{5x^2}{6}-\dfrac{21x}{4}+\dfrac{1}{6}\). Tìm số dư khi chia \(P\left(x\right)\) cho \(2x-5\).
Lời giải:
Theo định lý Bê-du về phép chia đa thức, số dư của $P(x)$ khi chia $2x-5$ là $P(\frac{5}{2})=\frac{5}{4}(\frac{5}{2})^3+\frac{5}{6}(\frac{5}{2})^2-\frac{21}{4}.\frac{5}{2}+\frac{1}{6}=\frac{377}{32}$
Đúng 1
Bình luận (0)
Tìm x:
\(a,\dfrac{8}{14}=\dfrac{x+1}{7}\) \(b,\dfrac{-4}{3}=\dfrac{5x+1}{-27}\)
\(a,\dfrac{8}{14}=\dfrac{x+1}{7}\\ \Leftrightarrow\dfrac{x+1}{7}=\dfrac{4}{7}\\ \Leftrightarrow x+1=4\\ \Leftrightarrow x=3\\ b,\dfrac{-4}{3}=\dfrac{5x+1}{-27}\\ \Leftrightarrow\dfrac{36}{-27}=\dfrac{5x+1}{-27}\\ \Leftrightarrow5x+1=36\\ \Leftrightarrow5x=35\\ \Leftrightarrow x=7\)
Đúng 2
Bình luận (0)
tìm X
\(\dfrac{5x}{1.6}+\dfrac{5x}{6.11}+\dfrac{5x}{11.16}+\dfrac{5x}{16.21}+\dfrac{5x}{21.26}+\dfrac{5x}{26.31}\)
\(\dfrac{5x}{1.6}+\dfrac{5x}{6.11}+\dfrac{5x}{11.16}+\dfrac{5x}{16.21}+\dfrac{5x}{21.26}+\dfrac{5x}{26.31}=1\)
\(=x\left(\dfrac{5}{1.6}+\dfrac{5}{6.11}+\dfrac{5}{11.16}+\dfrac{5}{16.21}+\dfrac{5}{21.26}+\dfrac{5}{26.31}\right)=1\)
\(=x\left(1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{16}+\dfrac{1}{16}-\dfrac{1}{21}+\dfrac{1}{21}-\dfrac{1}{26}+\dfrac{1}{26}-\dfrac{1}{31}\right)=1\)
\(=x\left(1-\dfrac{1}{31}\right)=1\)
\(\Rightarrow x=1:\left(1-\dfrac{1}{31}\right)=\dfrac{31}{30}\)
Đúng 1
Bình luận (1)