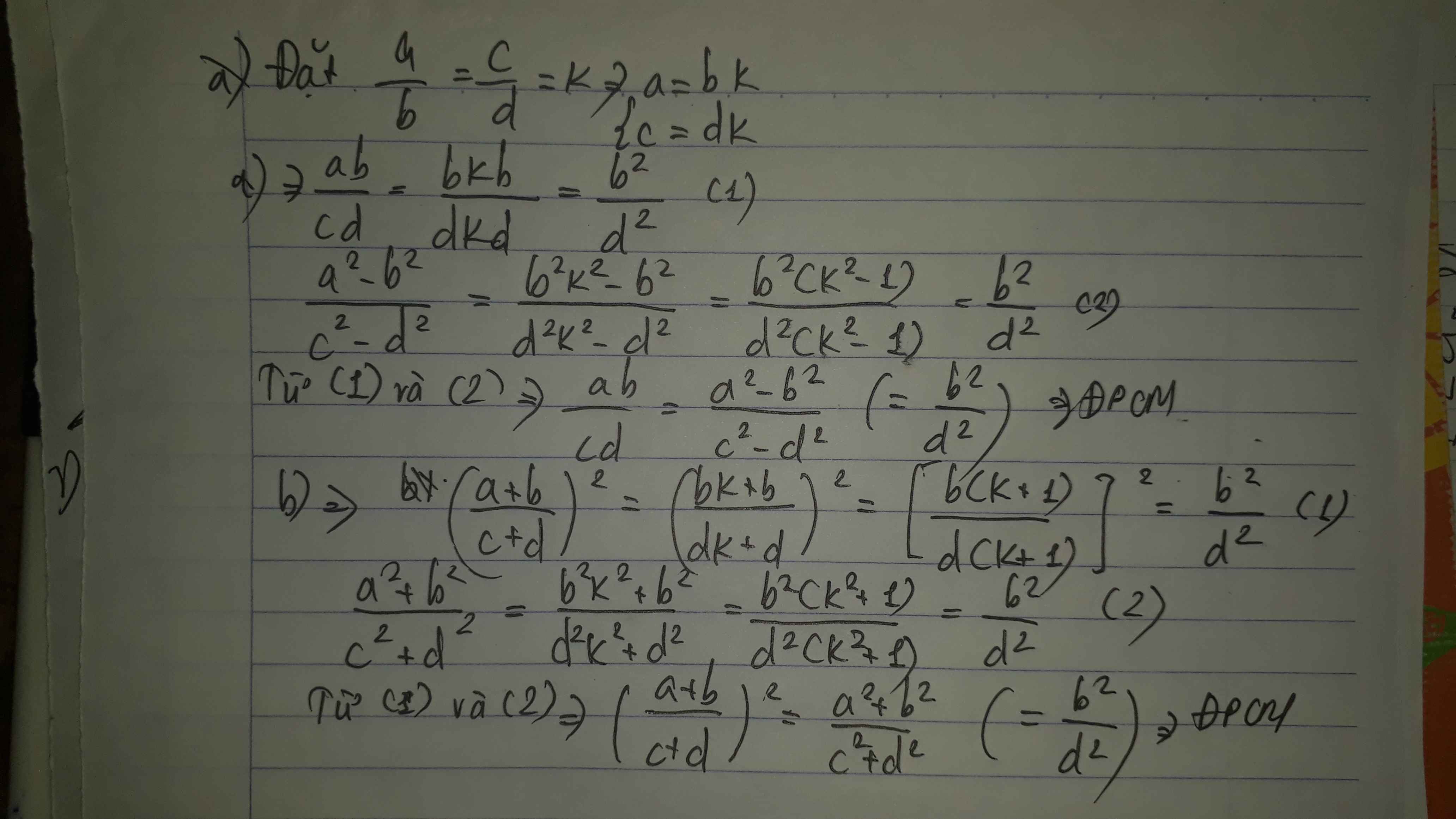Ta có:

\(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)

a) \(\dfrac{3a+5c}{3b+5d}=\dfrac{3\cdot bk+5\cdot dk}{3b+5d}=\dfrac{k\left(3b+5d\right)}{3b+5d}=k\) (1)

\(\dfrac{a-2c}{b-2d}=\dfrac{bk-2dk}{b-2d}=\dfrac{k\left(b-2d\right)}{b-2d}=k\) (2)

Từ (1) và (2) \(\Rightarrow\dfrac{3a+5c}{3b+5d}=\dfrac{a-2c}{b-2d}\left(dpcm\right)\)

b) \(\dfrac{a^2-b^2}{ab}=\dfrac{\left(bk\right)^2-b^2}{bk\cdot b}=\dfrac{b^2k^2-b^2}{b^2k}=\dfrac{b^2\left(k-1\right)}{b^2k}=\dfrac{k-1}{k}\)(1)

\(\dfrac{c^2-d^2}{cd}=\dfrac{\left(dk\right)^2-d^2}{dk\cdot d}=\dfrac{d^2k^2-d^2}{d^2k}=\dfrac{d^2\left(k-1\right)}{d^2k}=\dfrac{k-1}{k}\) (2)

Từ (1) và (2) \(\Rightarrow\dfrac{a^2-b^2}{ab}=\dfrac{c^2-d^2}{cd}\left(dpcm\right)\)

c) \(\left(\dfrac{a+b}{c+d}\right)^3=\left(\dfrac{bk+b}{dk+d}\right)^3=\dfrac{b^3\left(k+1\right)^3}{d^3\left(k+1\right)^3}=\dfrac{b^3}{d^3}\) (1)

\(\dfrac{a^3+b^3}{c^3+d^3}=\dfrac{\left(bk\right)^3+b^3}{\left(dk\right)^3+d^3}=\dfrac{b^3k^3+b^3}{d^3k^3+d^3}=\dfrac{b^3\left(k^3+1\right)}{d^3\left(k^3+1\right)}=\dfrac{b^3}{d^3}\) (2)

Từ (1) và (2) \(\Rightarrow\left(\dfrac{a+b}{c+d}\right)^3=\dfrac{a^3+b^3}{c^3+d^3}\left(dpcm\right)\)

Cứu mình với mình đang cần gấp!~

giúp mình câu d) luôn nha phong

cảm ơn phong nha

Bài 2: 

Đặt a/b=c/d=k

=>a=bk; c=dk

a: \(\dfrac{a}{a+b}=\dfrac{bk}{bk+b}=\dfrac{k}{k+1}\)

\(\dfrac{c}{c+d}=\dfrac{dk}{dk+d}=\dfrac{k}{k+1}\)

Do đó: \(\dfrac{a}{a+b}=\dfrac{c}{c+d}\)

b: \(\dfrac{7a^2+5ac}{7a^2-5ac}=\dfrac{7\cdot b^2k^2+5\cdot bk\cdot dk}{7\cdot b^2k^2-5\cdot bk\cdot dk}\)

\(=\dfrac{7b^2k^2+5bdk^2}{7b^2k^2-5bdk^2}=\dfrac{7b^2+5bd}{7b^2-5bd}\)(đpcm)

Từ \(\dfrac{a}{b}=\dfrac{c}{d}\)

=> \(\dfrac{a}{c}=\dfrac{b}{d}\)

=> \(\dfrac{a}{c}\).\(\dfrac{b}{d}=\dfrac{ab}{cd}=\dfrac{a}{c}\).\(\dfrac{a}{c}=\dfrac{b}{d}\).\(\dfrac{b}{d}\) \(=\dfrac{a^2}{c^2}=\dfrac{b^2}{d^2}\) (1)

Áp dụng t/c dãy tỉ số bằng nhau:

\(\dfrac{a^2}{c^2}=\dfrac{b^2}{d^2}=\dfrac{a^2-b^2}{c^2-d^2}\) (2)

=> \(\dfrac{a^2-b^2}{c^2-d^2}=\dfrac{ab}{cd}\)

=> \(\dfrac{a^2-b^2}{ab}=\dfrac{c^2-d^2}{cd}\) (ĐPCM)

\(\dfrac{a}{b}=\dfrac{c}{d}\\ \Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\\ \Rightarrow\dfrac{a^2}{c^2}=\dfrac{b^2}{d^2}=\dfrac{a^2-b^2}{c^2-d^2}\\ \dfrac{a^2}{c^2}=\dfrac{a}{c}.\dfrac{a}{c}=\dfrac{a}{c}.\dfrac{b}{d}=\dfrac{ab}{cd}\\ \Rightarrow\dfrac{ab}{cd}=\dfrac{a^2-b^2}{c^2-d^2}\)

Có thể dùng cách khác:v

a)\(\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow\dfrac{a}{c}=\dfrac{b}{d}=t\)(với t là 1 số thực bất kì thỏa mãn)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{c}.\dfrac{b}{d}=\dfrac{ab}{cd}=t^2\\\dfrac{a^2}{c^2}=\dfrac{b^2}{d^2}=\dfrac{a^2-b^2}{c^2-d^2}=t^2\end{matrix}\right.\Rightarrowđpcm\)

Tương tự:v

\(\dfrac{a}{b}=\dfrac{c}{d}=k\)

=>a=bk và c=dk

ta có \(\dfrac{a^2-b^2}{c^2-d^2}=\dfrac{\left(bk\right)^2-b^2}{\left(dk\right)^2-d^2}=\dfrac{b^2k^2-b^2}{d^2k^2-d^2}=\dfrac{b^2\left(k^2-1\right)}{d^2\left(k^2-1\right)}=\dfrac{b^2}{d^2}\)\(\dfrac{ab}{cd}=\dfrac{bk.b}{bk.d}=\dfrac{b^2}{d^2}\)

=>\(\dfrac{ab}{cd}=\dfrac{a^2-b^2}{c^2-d^2}\) (cùng =\(\dfrac{b^2}{d^2}\) ) (đpcm)

\(\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow\dfrac{a}{c}=\dfrac{b}{d}\)

Đặt: \(\dfrac{a}{c}=\dfrac{b}{d}=t\)

a) \(\left\{{}\begin{matrix}\dfrac{ab}{cd}=t^2\\\dfrac{a^2}{c^2}=\dfrac{b^2}{d^2}=\dfrac{a^2-b^2}{c^2-d^2}\end{matrix}\right.\Rightarrowđpcm\)

b) \(\left\{{}\begin{matrix}\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}\Leftrightarrow\left(\dfrac{a+b}{c+d}\right)^2=t^2\\\dfrac{a^2}{c^2}=\dfrac{b^2}{d^2}=\dfrac{a^2+b^2}{c^2+d^2}=t^2\end{matrix}\right.\Rightarrowđpcm\)

Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k:\)

Nên a=kb, c=kd

Do đó: \(\dfrac{ab}{cd}=\dfrac{kbb}{kdd}=\dfrac{kb^2}{kd^2}=\dfrac{b^2}{d^2}\)

Và: \(\dfrac{a^2-b^2}{c^2-d^2}=\dfrac{\left(kb\right)^2-b^2}{\left(kd\right)^2-d^2}=\dfrac{b^2\left(k^2-1\right)}{d^2\left(k^2-1\right)}=\dfrac{b^2}{d^2}\)

Vậy \(\dfrac{ab}{cd}=\dfrac{a^2-b^2}{c^2-d^2}\)

Ta có: \(\left(\dfrac{a+b}{c+d}\right)^2=\dfrac{\left(a+b\right)^2}{\left(c+d\right)^2}=\dfrac{\left(kb+b\right)^2}{\left(kd+d\right)^2}=\dfrac{\left[\left(k+1\right)b\right]^2}{\left[\left(k+1\right)d\right]^2}=\dfrac{\left(k+1\right)^2.b^2}{\left(k+1\right)^2.d^2}=\dfrac{b^2}{d^2} \)

\(\dfrac{a^2+b^2}{c^2+d^2}=\dfrac{\left(kb\right)^2+b^2}{\left(kd\right)^2+d^2}=\dfrac{\left(k^2+1\right)b^2}{\left(k^2+1\right)d^2}=\dfrac{b^2}{d^2}\)

Vậy \(\left(\dfrac{a+b}{c+d}\right)^2=\dfrac{a^2+b^2}{c^2+d^2}\)

Đặt: \(\dfrac{a}{b}=\dfrac{c}{d}=k\)

\(\Rightarrow a=bk,c=dk\)

Ta có VT:

\(\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}=\dfrac{\left(bk-b\right)^2}{\left(dk-d\right)^2}\)

\(=\dfrac{b^2\left(k-1\right)^2}{d^2\left(k-1\right)^2}=\dfrac{b^2}{d^2}\) (1)

VT: \(\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot d}=\dfrac{b^2k}{d^2k}=\dfrac{b^2}{d^2}\) (2)

Từ (1) và (2) 

\(\Rightarrow\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}=\dfrac{ab}{cd}\left(đpcm\right)\)

Có: \(\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow ab=cd\Leftrightarrow\dfrac{a}{c}=\dfrac{b}{d}\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a-b}{c-d}\)\(\Leftrightarrow\left(\dfrac{a}{c}\right)^2=\left(\dfrac{b}{d}\right)^2=\dfrac{ab}{cd}=\left(\dfrac{a-b}{c-d}\right)^2\)

Vậy...

d: Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)

\(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)

Ta có: \(\dfrac{3c^2+5a^2}{3d^2+5b^2}=\dfrac{3\cdot\left(dk\right)^2+5\cdot\left(bk\right)^2}{3d^2+5b^2}=k^2\)

\(\dfrac{c^2}{d^2}=\dfrac{\left(dk\right)^2}{d^2}=k^2\)

Do đó: \(\dfrac{3c^2+5a^2}{3d^2+5b^2}=\dfrac{c^2}{d^2}\)