Cho h/s y =(2m-5)x +3 với m# 5/2 có đồ thị là đg thẳg d .Tìm m để :
a, (d) luôn cắt đg thẳng 2x -4y -3 =0
b, (d) cắt đg thẳng 2x +y = -3 tại điểm có hoàh độ = -2
C, cminh (d) luôn đi qua 1 điẻm cố định trên trục tug
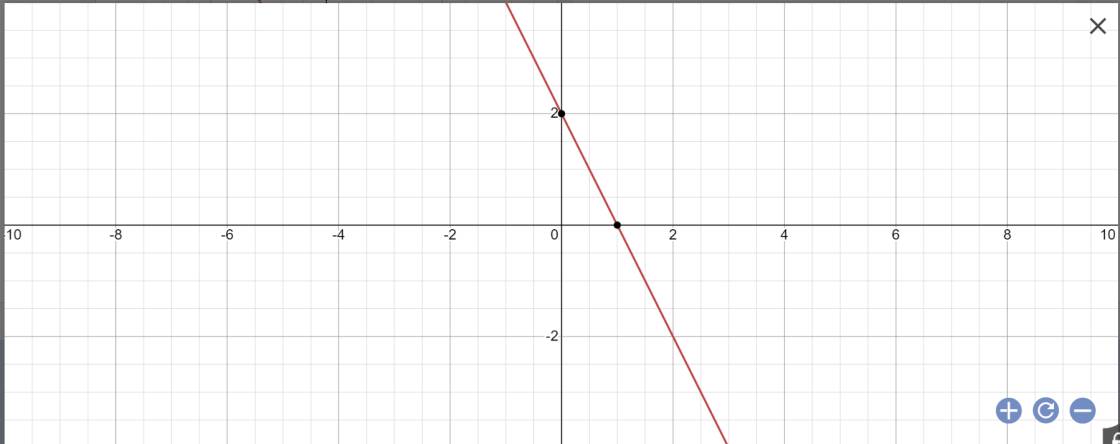
1) Cho h/s bậc nhất y=(m-3)x+2m ( 1 )
a) Tìm m để h/s trên là h/s bậc nhất
b) Tìm m để đồ thị h/s ( 1 ) song song với đồ thị h/s y=-2x=3
c) Vẽ đồ thị với giá trị m vừa mới tim được ở câu b
2) Cho tam giác ABC, đường cao AH, biết AB = 3cm, AC = 4cm, BC = 5cm
a) Chứng minh tam giác ABC vuông tại A
b) Tính đường cao AH
c) Diện tích AHC
Bài 2:
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot5=3\cdot4=12\)
=>AH=12/5=2,4(cm)
c: ΔAHC vuông tại H
=>\(AH^2+HC^2=AC^2\)
=>\(HC^2=4^2-2,4^2=10,24\)
=>HC=3,2(cm)
ΔAHC vuông tại H
=>\(S_{HAC}=\dfrac{1}{2}\cdot HA\cdot HC=\dfrac{1}{2}\cdot3,2\cdot2,4=1,2\cdot3,2=3,84\left(cm^2\right)\)
Bài 1:
a: Để (1) là hàm số bậc nhất thì m-3<>0
=>m<>3
b: Sửa đề: y=-2x+3
Để (1)//y=-2x+3 thì \(\left\{{}\begin{matrix}m-3=-2\\2m< >3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=1\\m< >\dfrac{3}{2}\end{matrix}\right.\)
=>m=1
c: Khi m=1 thì (d): \(y=\left(1-3\right)x+2\cdot1=-2x+2\)
Cho hàm số: y = (m-1)x + 2m - 3 (d)
Tìm m để S tam giác tạo bởi d với 2 trục bằng 5.
Cho hàm số y = mx^3 - 2(m^2 + 1)x^2 + 2m^2 - m. Tìm các điểm cố định mà đồ thị hàm sô đã cho luon đi qua với mọi m.
\(y=mx^3-2m^2x^2-2x^2+2m^2-m\)
\(\Leftrightarrow2m^2\left(1-x^2\right)+m\left(x^3-1\right)-2x^2-y=0\)
Gọi \(\left(x_0;y_0\right)\) là điểm cố định mà đồ thị hàm số luôn đi qua thì:
\(\left\{{}\begin{matrix}1-x+0^2=0\\x_0^3-1=0\\-2x_0^2-y=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_0=1\\y_0=-2\end{matrix}\right.\)
Cho hàm số y = f(x) = (m2−2m+3).x2
Chứng tỏ hàm số đồng biến khi x > 0, từ đó hãy so sánh f(\(\sqrt{2}\)) và f(\(\sqrt{5}\))
\(a=m^2-2m+3=\left(m-1\right)^2+2>0\) \(\forall m\)
\(\Rightarrow\) Hàm số đồng biến khi \(x>0\)
Vậy \(x_1>x_2>0\Rightarrow f\left(x_1\right)>f\left(x_2\right)\)
Mà \(\sqrt{5}>\sqrt{2}>0\Rightarrow f\left(\sqrt{5}\right)>f\left(\sqrt{2}\right)\)
cho h/s y=(m-1)x +2m
a; Vẽ đồ thị h/s với m=-1. Gọi giao điểm của đồ thị vừa vẽ là M và N. tính đt tam giác OMN
cho hàm số y = (m - 2)x - 2m + 4 (d)
Gọi giao điểm (d) với Ox và Oy lần lượt là A và B. Tìm m để S△OAB = 3
Cho h/s y= (m-1)x +2m
a;Vẽ đồ thị h/s với m=-1.
b; gọi giao điểm của 2 giao điểm là M và N. tính dt tam giác MON
cho hàm số
\(y=\frac{x+2m}{\sqrt[]{}x+3-4m}+\sqrt[]{2m+3-x}\)
a) tìm x để hàm số xác định trên -1,2
b)tìm m để hàm só xác định trên [-1 , 2]
Cho 2 hàm số bậc nhất. y=(m+3)x-1 và y=(1-2m)x+5. Với giá trị nào của m để hai hàm số trên song song .cắt nhau. trùng nhau
Gọi (d):y=(m+3)x-1
(d');y=(1-2m)x+5
Để đồ thị hàm số (d) và (d') song song thì
\(\left\{{}\begin{matrix}m+3=1-2m\\-1\ne5\left(lu\text{ô}n\text{đ}\text{úng}\right)\end{matrix}\right.\)
⇔3m=-2
⇔m=\(\frac{-2}{3}\)
Vậy đồ thị hàm số (d) và (d') song song thì m=\(\frac{-2}{3}\)
Để đồ thị hàm số (d) và (d') cắt nhau thì
(m+3)(1-2m)=-1
⇔-2m2-5m+4=0
⇔\(m^2+\frac{5}{2}m-2=0\)
⇔\(\left(m+\frac{5}{4}\right)^2=\frac{57}{16}\)
⇔\(\left[{}\begin{matrix}m=\frac{-5+\sqrt[]{57}}{4}\\m=\frac{-5-\sqrt[]{57}}{4}\end{matrix}\right.\)
Vậy đồ thị hàm số (d) và (d') cắt nhau thì mϵ\(\left\{\frac{-5+\sqrt[]{57}}{4};\frac{-5-\sqrt[]{57}}{4}\right\}\)
Để đồ thị hàm số (d) và (d') trùng nhau thì
\(\left\{{}\begin{matrix}m+3=1-2m\\-1=5\left(v\text{ô}l\text{í}\right)\end{matrix}\right.\)
Vậy không có giá trị m thỏa mãn để đồ thị hàm số (d) và (d') trùng nhau