1)Cho hình vẽ : biết widehat{A} + widehat{B}+widehat{C}180 độ. CMR Ax song song CY
Đọc tiếp
1)Cho hình vẽ : biết \(\widehat{A}\) + \(\widehat{B}\)+\(\widehat{C}\)=180 độ. CMR Ax song song CY
Những câu hỏi liên quan
Cho tam giác ABC có \(\widehat{B}\)=70độ; góc C=40 độ. Vẽ tia Cx là tia đối của tia CB. Vẽ Cy là tia phân giác \(\widehat{ACx}\)
a) Tính \(\widehat{ACx};\widehat{xCy}\)
b) CMR: \(AB\) song song Cy
8 tháng 10 2021 lúc 8:20
1. Cho hình vẽ . Biết widehat{A} 135( độ ) , widehat{B} 45( độ ) , widehat{D} 55( độ )a) Đường thẳng a có song song với đường b không ? Vì sao ? b) Tính số đo góc C_1
Đọc tiếp
1. Cho hình vẽ . Biết \(\widehat{A}\) = 135'( độ ) , \(\widehat{B}\) = 45'( độ ) , \(\widehat{D}\) = 55'( độ )
a) Đường thẳng a có song song với đường b không ? Vì sao ?
b) Tính số đo góc C\(_1\)
a) A + B = 180 độ
Mà A và B là cặp góc trong cùng phía
=> a//b
b) a//b
=> D = C (so le trong)
=> C = 55 độ
Đúng 0
Bình luận (0)
1.Cho hình 16:a) Cho biết Ax//Cy.So sánh widehat{ABC} với widehat{A} và widehat{C}b) Cho biết widehat{ABC}widehat{A} vàwidehat{C} . Chứng tỏ rằng Ax// Cy x y B A C Hình 16 Hình 16
Đọc tiếp
1.Cho hình 16:
a) Cho biết \(Ax//Cy.So\) \(sánh \)\(\widehat{ABC}\) với \(\widehat{A}\) và \(\widehat{C}\)
b) Cho biết \(\widehat{ABC}\)=\(\widehat{A}\) và\(\widehat{C}\) . Chứng tỏ rằng \(Ax//\) Cy
6 tháng 10 2021 lúc 7:53
Cho hình vẽ . Biết widehat{A} 147( độ ) , widehat{B} 33( độ ) , widehat{D} 59( độ )a) Đường thẳng a có song song vưới đường thẳng b không ? Vì sao ?b) Tính số đo góc C _1 ?
Đọc tiếp
Cho hình vẽ . Biết \(\widehat{A}\) = 147'( độ ) , \(\widehat{B}\) = 33'( độ ) , \(\widehat{D}\) = 59'( độ )
a) Đường thẳng a có song song vưới đường thẳng b không ? Vì sao ?
b) Tính số đo góc C \(_1\) ?
\(\widehat{D1}=\widehat{C1}\left(soletrong\right)\)
\(\widehat{A1}+\widehat{B1}=180^o\left(bùnhau\right)\)
\(\Rightarrow\)a//b
\(\widehat{D1}=\widehat{C1}\left(soletrong\right)=59^o\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có widehat{A}80 độ, widehat{C}50 độ. Trên tia đối của tia Ac lấy điểm D, vẽ widehat{CDE} so le trong với widehat{C}và bằng widehat{C}.Gọi Am là tia phân giác của widehat{BAD}.Chứng minh DE song song với Am và BC song song với Am (Biết widehat{A}+widehat{B}+widehat{C}180 độ)
Đọc tiếp
Cho tam giác ABC có \(\widehat{A}\)=80 độ, \(\widehat{C}\)=50 độ. Trên tia đối của tia Ac lấy điểm D, vẽ \(\widehat{CDE}\) so le trong với \(\widehat{C}\)và bằng \(\widehat{C}\).Gọi Am là tia phân giác của \(\widehat{BAD}\).Chứng minh DE song song với Am và BC song song với Am (Biết \(\widehat{A}\)+\(\widehat{B}\)+\(\widehat{C}\)=180 độ)
a) Ta có: \(\widehat{EDC}=\widehat{BCD}\left(gt\right)\)
Mà \(\widehat{BCD}=50^0\left(gt\right)\)
=> \(\widehat{EDC}=50^0.\)
Lại có: \(\widehat{DAB}\) là góc ngoài tại đỉnh A của \(\Delta ABC.\)
=> \(\widehat{DAB}=180^0-\widehat{A}=180^0-80^0\)
=> \(\widehat{DAB}=100^0.\)
Vì \(Am\) là tia phân giác của \(\widehat{DAB}\left(gt\right)\)
=> \(\widehat{DAm}=\widehat{mAB}=\frac{\widehat{DAB}}{2}=\frac{100^0}{2}=50^0.\)
Mà \(\widehat{EDC}=50^0\left(cmt\right)\)
=> \(\widehat{EDC}=\widehat{DAm}\)
Mà 2 góc này nằm ở vị trí so le trong.
=> \(DE\) // \(Am.\)
b) Ta có:
\(\left\{{}\begin{matrix}\widehat{DAm}=50^0\left(cmt\right)\\\widehat{DCB}=50^0\left(gt\right)\end{matrix}\right.\)
=> \(\widehat{DAm}=\widehat{DCB}\)
Mà 2 góc này nằm ở vị trí đồng vị.
=> \(Am\) // \(BC\left(đpcm\right).\)
Chúc bạn học tốt!
Đúng 0
Bình luận (0)
Cho hình vẽ dưới đây biết a // (song song) b và widehat{M1} - widehat{N2} 50◦ Tính widehat{M2} và widehat{N2}
Đọc tiếp
Cho hình vẽ dưới đây biết a // (song song) b và \(\widehat{M1} - \widehat{N2}\) = 50◦
Tính \(\widehat{M2} và \widehat{N2}\)
Cho tam giác ABC có \(\widehat{A}=180^o-3\times\widehat{C}\); \(\widehat{B}=70^o\)
Vẽ tia phân giác \(\widehat{B}\) cắt AC tại E. Qua E kẻ đường thẳng song song BC cắt AB tại D.CMR: ED là tia phân giác của \(\widehat{AED}\)
Ta có \(\widehat{A}+\widehat{ABC}+\widehat{C}=180^0\Rightarrow180^0-3\widehat{C}+\widehat{C}=180^0-70^0=110^0\)
\(\Rightarrow2\widehat{C}=70^0\Rightarrow\widehat{C}=35^0\Rightarrow\widehat{A}=180^0-3\cdot35^0=75^0\)
Ta có BE là p/g nên \(\widehat{B_1}=\widehat{B_2}=\dfrac{1}{2}\widehat{ABC}=35^0\)
Mà \(ED//BC\) nên \(\widehat{B_2}=\widehat{E_2}=35^0\left(so.le.trong\right)\left(1\right)\)
Ta có \(ED//BC\Rightarrow\widehat{E_1}=\widehat{C}=35^0\left(đồng.vị\right)\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow\widehat{E_1}=\widehat{E_2}\left(=35^0\right)\)
Vậy ...
Đúng 2
Bình luận (0)
Cho Hình 3.50, trong đó hai tia Ax và By nằm trên hai đường thẳng song song. Chứng minh rằng \(\widehat C = \widehat A + \widehat B\)
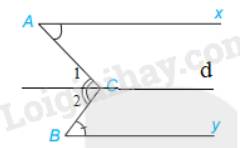
Qua C kẻ đường thẳng d song song với Ax
Vì Ax // By nên d // By
Vì d // Ax nên \(\widehat A = \widehat {{C_1}}\)(2 góc so le trong)
Vì d // By nên \(\widehat B = \widehat {{C_2}}\) (2 góc so le trong)
Mà \(\widehat C = \widehat {{C_1}} + \widehat {{C_2}}\)
Vậy \(\widehat C = \widehat A + \widehat B\)(đpcm)
Đúng 0
Bình luận (0)
Giải giúp mk 2 bài toán này nha1. Cho tam giác ABC tia phân giác Ax của góc BAC. Qua C vẽ tia Cy. Song song với tia Ax tại D.Chứng minh widehat{ADB}widehat{DCA}frac{widehat{BAC}}{2} 2. Cho tam giác ABC, góc B góc C. Vẽ tia Ax song song với cạnh BC, tia AD là tia đối của tia AB.Chứng minh rằng Ax là tia phân giác của góc CADCác bn vẽ hình rồi giải giúp mk nha CẢM ƠN CÁC BẠN NHIỀU
Đọc tiếp
Giải giúp mk 2 bài toán này nha
1. Cho tam giác ABC tia phân giác Ax của góc BAC. Qua C vẽ tia Cy. Song song với tia Ax tại D.
Chứng minh \(\widehat{ADB}=\widehat{DCA}=\frac{\widehat{BAC}}{2}\)
2. Cho tam giác ABC, góc B = góc C. Vẽ tia Ax song song với cạnh BC, tia AD là tia đối của tia AB.
Chứng minh rằng Ax là tia phân giác của góc CAD
Các bn vẽ hình rồi giải giúp mk nha
CẢM ƠN CÁC BẠN NHIỀU
Cho hình vẽ , biết \(\widehat{CBy}>\widehat{ACB}\)
CMR : Nếu Ax // By thì \(\widehat{CAx}+\widehat{CBy}-\widehat{ACB}=180^0\)