Giải giúp mình bài này với:Cân bằng phương trình
1) CnH2n + O2 \(\rightarrow\) CO2 + H2O
2) Fe2O3 + CO \(\rightarrow\) CO2 +Fe
Mình cần gấp![]() Cảm ơn!!!
Cảm ơn!!!![]()
Có ai giúp mình giải bài hóa này với
Cân bằng phương trình phản ứng:
\(FeS_2+O_2\rightarrow SO_2+Fe_2O_3\)
Chỉ RÕ cách để làm bước 2 nha , nó lằng nhằng lắm
Biết ngay là chờ đợi trong vô vọng mà
4 FeS2 + 11 O2 ----------> 8 SO2 + 2 Fe203
\(2FeS_2+3O_2->3SO_2+Fe_2O_3\)
Lập phương trình hóa học của các phản ứng sau:
1) CnH2n + O2 → CO2 + H2O
2) CnH2n + 2 + O2 → CO2 + H2O
3) CnH2n - 2 + O2 → CO2 + H2O
4) CnH2n - 6 + O2 → CO2 + H2O
5) CnH2n + 2O + O2 → CO2 + H2O
6) CxHy + O2 → CO2 + H2O
7) CxHyOz + O2 → CO2 + H2O
8) CxHyOzNt + O2 → CO2 + H2O + N2
9) CHx + O2 → COy + H2O
10) FeClx + Cl2 → FeCl3
Ai giúp em với ạ ... Em cảm ơn ...
giúp với:
Cân bằng các phương trình hóa học sau chứa ẩn
1) FexOy + H2 → Fe + H2O
2) FexOy + HCl → FeCl2y/x + H2O
\(Fe_xO_y+yH_2\underrightarrow{^{^{t^0}}}xFe+yH_2O\)
\(Fe_xO_y+2yHCl\rightarrow xFeCl_{\dfrac{2y}{x}}+yH_2O\)
GIÚP MÌNH GIẢI BÀI NÀY VỚI Ạ
ĐỀ : GIẢI CÁC HỆ PHƯƠNG TRÌNH SAU
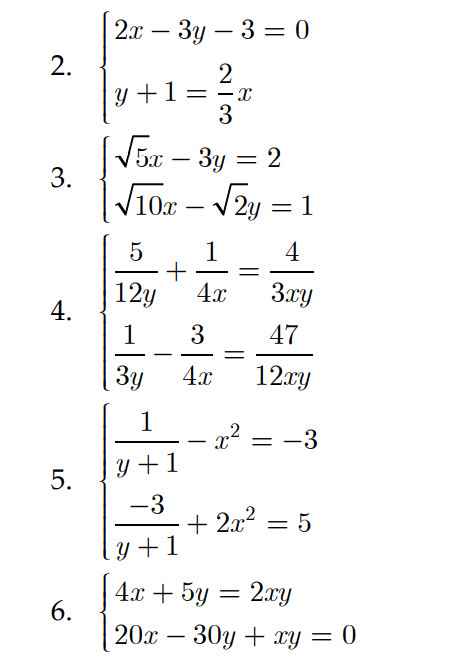
Giải các phương trình giúp mình bài này vớii mình cảm ơn trước nha
\(9,PT\Leftrightarrow x-6=3x-7\left(x\ge6\right)\\ \Leftrightarrow x=\dfrac{1}{2}\left(ktm\right)\\ \Leftrightarrow x\in\varnothing\\ 10,PT\Leftrightarrow3x-2=4x^2-4x+1\left(x\le\dfrac{1}{2}\right)\\ \Leftrightarrow4x^2-7x+3=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{3}{4}\end{matrix}\right.\left(ktm\right)\Leftrightarrow x\in\varnothing\\ 11,PT\Leftrightarrow\sqrt{x^2+x-1}=2-x\left(x\le2\right)\\ \Leftrightarrow x^2+x-1=x^2-4x+4\\ \Leftrightarrow5x=5\Leftrightarrow x=1\left(tm\right)\\ 12,PT\Leftrightarrow\left(\sqrt{20-x}-4\right)+\left(\sqrt{x+5}-3\right)=0\left(5\le x\le20\right)\\ \Leftrightarrow\dfrac{4-x}{\sqrt{20-x}+4}+\dfrac{x-4}{\sqrt{x+5}+3}=0\\ \Leftrightarrow\left(x-4\right)\left(\dfrac{1}{\sqrt{x+5}+3}-\dfrac{1}{\sqrt{20-x}+4}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\\dfrac{1}{\sqrt{x+5}+3}=\dfrac{1}{\sqrt{20-x}+4}\left(1\right)\end{matrix}\right.\\ \left(1\right)\Leftrightarrow\sqrt{x+5}+3=\sqrt{20-x}+4\\ \Leftrightarrow\left(\sqrt{x+5}-4\right)-\left(\sqrt{20-x}-3\right)=0\\ \Leftrightarrow\dfrac{x-11}{\sqrt{x+5}+4}+\dfrac{x-11}{\sqrt{20-x}+3}=0\\ \Leftrightarrow\left(x-11\right)\left(\dfrac{1}{\sqrt{x+5}+4}+\dfrac{1}{\sqrt{20-x}+3}\right)=0\\ \Leftrightarrow x=11\left(\dfrac{1}{\sqrt{x+5}+4}+\dfrac{1}{\sqrt{20-x}+3}>0\right)\\ \text{Vậy PT có nghiệm }x\in\left\{4;11\right\}\)
\(13,PT\Leftrightarrow\sqrt{x-1}+\sqrt{3x-2}=\sqrt{5x+1}\left(x\ge-\dfrac{1}{5}\right)\\ \Leftrightarrow4x-3+2\sqrt{\left(x-1\right)\left(3x-2\right)}=5x+1\\ \Leftrightarrow x+4=2\sqrt{3x^2-5x+2}\\ \Leftrightarrow x^2+8x+16=12x^2-20x+8\\ \Leftrightarrow11x^2-28x-8=0\\ \Delta'=14^2+8\cdot11=284\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{14-2\sqrt{71}}{11}\\x=\dfrac{14+2\sqrt{71}}{11}\end{matrix}\right.\)
\(14,ĐK:x\ge-1\)
Đặt \(\sqrt{x+1}=a\ge0\)
\(PT\Leftrightarrow2\sqrt{a^2-1+2a}-a=4\\ \Leftrightarrow2\sqrt{a^2+2a-1}=a+4\\ \Leftrightarrow4a^2+8a-4=a^2+8a+16\\ \Leftrightarrow3a^2-20=0\\ \Leftrightarrow a^2=\dfrac{20}{3}\Leftrightarrow x+1=\dfrac{20}{3}\Leftrightarrow x=\dfrac{17}{3}\left(tm\right)\)
\(15,ĐK:-3\le x\le6\)
Đặt \(\sqrt{x+3}+\sqrt{6-x}=a\ge0\)
\(\Leftrightarrow\dfrac{a^2-9}{2}=\sqrt{\left(x+3\right)\left(6-x\right)}\\ PT\Leftrightarrow a-\dfrac{a^2-9}{2}=3\\ \Leftrightarrow2a-a^2+9=6\\ \Leftrightarrow a^2-2a-3=0\\ \Leftrightarrow a=3\left(a\ge0\right)\\ \Leftrightarrow\sqrt{x+3}+\sqrt{6-x}=3\\ \Leftrightarrow\sqrt{x+3}-3+\sqrt{6-x}=0\\ \Leftrightarrow\dfrac{x-6}{\sqrt{x+3}+3}-\dfrac{x-6}{\sqrt{6-x}}=0\\ \Leftrightarrow\left[{}\begin{matrix}x=6\left(tm\right)\\\dfrac{1}{\sqrt{x+3}+3}=\dfrac{1}{\sqrt{6-x}}\left(1\right)\end{matrix}\right.\\ \left(1\right)\Leftrightarrow\sqrt{x+3}+3=\sqrt{6-x}\\ \Leftrightarrow\sqrt{x+3}-\left(\sqrt{6-x}-3\right)=0\\ \Leftrightarrow\dfrac{x+3}{\sqrt{x+3}}+\dfrac{x+3}{\sqrt{6-x}+3}=0\\ \Leftrightarrow x=-3\left(\dfrac{1}{\sqrt{x+3}}+\dfrac{1}{\sqrt{6-x}+3}>0\right)\\ \text{Vậy PT có nghiệm }x\in\left\{6;-3\right\}\)
\(16,\) Đặt \(\sqrt{x^2-6x+6}=a\ge0\)
\(PT\Leftrightarrow a^2+3=4a\\ \Leftrightarrow a^2-4a+3=0\\ \Leftrightarrow\left[{}\begin{matrix}a=1\\a=3\end{matrix}\right.\)
Với \(a=1\Leftrightarrow x^2-6x+5=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
Với \(a=3\Leftrightarrow x^2-6x-3=0\Leftrightarrow\left[{}\begin{matrix}x=3+2\sqrt{3}\\x=3-2\sqrt{3}\end{matrix}\right.\)
Vậy PT có nghiệm \(x\in\left\{1;5;3+2\sqrt{3};3-2\sqrt{3}\right\}\)
Hoàn thành các phương trình hoá học sau
P+O2-->
K+O2-->
Fe+O2-->
C3H8+O2-->
H2S+O2-->
C2H6O + O2 -->
C2H7N +O2 -->
CnH2n+2 +O2-->
4P+5O2--to>2P2O5
4K+O2--to>2K2O
3Fe+2O2-to->Fe3O4
C3H8+5O2--to>3CO2+4H2O
H2S+\(\dfrac{3}{2}\)O2-to-> SO2+H2O
C2H6O +3 O2 -to->2CO2+3H2O
\(4P+5O_2\underrightarrow{t^o}2P_2O_5\\ 4K+O_2\underrightarrow{t^o}2K_2O\\ 3Fe+2O_2\underrightarrow{t^o}Fe_3O_4\\ C_3H_8+5O_2\underrightarrow{t^o}3CO_2+4H_2O\\ 2H_2S+3O_2\underrightarrow{t^o}2H_2O+2SO_2\\ C_2H_6O+3O_2\underrightarrow{t^o}2CO_2+3H_2O\\ 4C_2H_7N+19O_2\underrightarrow{t^o}8CO_2+14H_2O+4NO_2\\ 2C_nH_{2n+2}+\left(3n+1\right)O_2\underrightarrow{t^o}2nCO_2+\left(2n+2\right)H_2O\)
Giúp mình bài này với
1 / Giải phương trình : 2x + 3 + x + 1 = 3x + 2y2 + 5x + 3 - 16 .
<=> 3x+4 = 2y2+8x-13 <=> -5x+17 = 2y2 (1)
điều kiện 17-5x \(\ge0< =>x\le\)\(\frac{17}{5}\)
(1) <=> y2=(17-5x):2 <=> y = \(\pm\sqrt{\frac{17-5x}{2}}\)
GIẢI BẤT PHƯƠNG TRÌNH |x-1|+|2-x| > 3
CÁC BẠN GIÚP MÌNH GIẢI BÀI NÀY VỚI
Cho phương trình: x2 – mx + m – 1 = 0 (1). Tìm m để phương trình (1) có hai nghiệm phân biệt x1 và x2 thoả mãn: x12 + 3x1x2 = 3x2 + 3m + 16.
giải giúp mình bài này với ạ, mình cảm ơn
\(m\left(sinx+cosx\right)+sin2x+m-1=0\). Tìm m để phương trình có nghiệm
(Giúp mình giải bài này với)