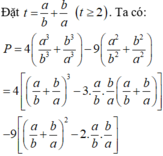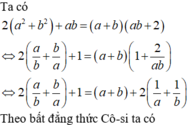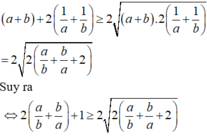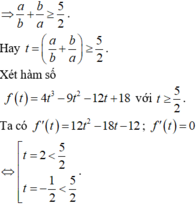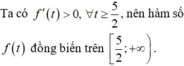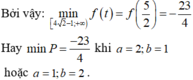CMR: \(\frac{a^4+b^4}{2}\)>= ab3 + a3b - a2b2

Những câu hỏi liên quan
CM: a4+b4≥a3b+ab3 (∀a,b)
\(a^4+b^4-a^3b-ab^3=a^3\left(a-b\right)-b^3\left(a-b\right)=\left(a-b\right)\left(a^3-b^3\right)=\left(a-b\right)\left(a-b\right)\left(a^2+ab+b^2\right)=\left(a-b\right)^2\left(a^2+ab+b^2\right)\)
Có: \(\left\{{}\begin{matrix}\left(a-b\right)^2\ge0\\a^2+ab+b^2>0\end{matrix}\right.\)
\(\Rightarrow a^4+b^4-a^3b-ab^3\ge0\)
\(\Rightarrow a^4+b^4\ge a^3b+ab^3\)
Đúng 0
Bình luận (0)
Áp dụng BĐT cosi với 2 số không âm:
`a^4+b^4+b^4+b^4>=4\root4{a^4b^12}=4|ab^3|>=4ab^3`
Hoàn toàn tương tự:
`b^4+a^4+a^4+a^4>=4a^3b`
`=>a^4+b^4+b^4+b^4+b^4+a^4+a^4+a^4>=4ab^3+4a^3b`
`<=>4(a^4+b^4)>=4(ab^3+a^3b)`
`<=>a^4+b^4>=ab^3+a^3b`
Đúng 0
Bình luận (0)
Tìm ab , biết :
ab + ab3 = 619 a3b : ab = 11 ( biết a < b )Tìm ab , biết :
ab + ab3 = 619ab + ab3 = 619 suy ra b phải = 6 vì 3
+ b = 9 nên b= 6 chuyển thành a6 + a63 suy ra a = 5 vì 6 + a = 1 vậy a = 5 cuyển thành 56 + 563 = 619
vậy ab = 56
2 .a3b : ab = 11 ( biết a < b )
cuyển thành 11 x ab = a3b mà 3 = a + b mà b lớn hơn a
nếu a = 3 thì b = 0
là sai
nếu a = 2 thì b = 1
là sai
nếu a = 1 thì b = 2 ( đúng yêu cầu )
ta thử a= 1 , b = 2 thì thành 132 : 12 = 11
vậy ab = 12
rồi nha bạn hih
Đúng 0
Bình luận (0)
ab; ab3; a3b là số hả bạn? nếu là số thì phải có gạch đầu chứ!!!
Đúng 0
Bình luận (0)
chắc bn ấy ko bit gạch hay bn ấy quên nhưng mk đảm bảo ab ,ab3,a3b là số
Đúng 0
Bình luận (0)
1.số ab3 chia hết cho 9 và lấy a-b =4. tìm số ab3
2.tìm y, biết :
(14,7 -y )x2/9 =1/3
1. Vì ab3 chia hết cho 9 nên ab= 51, đồng thời 5-1=4
Vậy ab=51
2. ( 14,7-y) = 1/3: 2/9
14,7-y = 3/2
y = 14,7-3/2
y = 14,7- 1,5
y = 13,2
Cho
a
.
b
∈
ℝ
;
a
,
b
0
; thỏa mãn
2
(
a
2
+
b
2
)
+
a
b
(...
Đọc tiếp
Cho a . b ∈ ℝ ; a , b > 0 ; thỏa mãn 2 ( a 2 + b 2 ) + a b = ( a + b ) ( a b + 2 ) . Giá trị nhỏ nhất của biểu thức P = 4 ( a 3 b 3 + b 3 a 3 ) - 9 ( a 2 b 2 + b 2 a 2 ) bằng
A. - 10
B. - 21 4
C. - 23 4
D. 23 4
a) cho x,y dương. CMR: \(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\)
b) cho a+b+c=1 CMR: \(\frac{a}{a+b^2}+\frac{b}{b+c^2}+\frac{c}{c+a^2}\le\frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
a/ \(\Leftrightarrow\frac{x+y}{xy}\ge\frac{4}{x+y}\Leftrightarrow\left(x+y\right)^2\ge4xy\)
\(\Leftrightarrow x^2+y^2-2xy\ge0\Leftrightarrow\left(x-y\right)^2\ge0\) (luôn đúng)
Vậy BĐT đã cho đúng
b/ \(\frac{a}{a+b^2}=\frac{a}{a\left(a+b+c\right)+b^2}=\frac{a}{a^2+b^2+a\left(b+c\right)}\le\frac{a}{2ab+a\left(b+c\right)}=\frac{1}{b+b+b+c}\)
\(\Rightarrow\frac{a}{a+b^2}=\frac{1}{b+b+b+c}\le\frac{1}{16}\left(\frac{1}{b}+\frac{1}{b}+\frac{1}{b}+\frac{1}{c}\right)=\frac{1}{16}\left(\frac{3}{b}+\frac{1}{c}\right)\)
Tương tự: \(\frac{b}{b+c^2}\le\frac{1}{16}\left(\frac{3}{c}+\frac{1}{a}\right)\) ; \(\frac{c}{c+a^2}\le\frac{1}{16}\left(\frac{3}{a}+\frac{1}{c}\right)\)
Cộng vế với vế:
\(VT\le\frac{1}{16}\left(\frac{4}{a}+\frac{4}{b}+\frac{4}{c}\right)=\frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
Dấu "=" xảy ra khi \(a=b=c=\frac{1}{3}\)
Đúng 0
Bình luận (0)
Cho a,b,c >0 abc=1. CMR \(\frac{a^4}{b^2\left(c+a\right)}+\frac{b^4}{c^2\left(a+b\right)}+\frac{c^4}{a^2\left(b+c\right)}\ge\frac{a+b+c}{2}\)
cho 3 số thực dương a,b,c
CMR: \(\frac{a^4}{\left(b+c\right)^2}+\frac{b^4}{\left(a+c\right)^2}+\frac{c^4}{\left(a+b\right)^2}\ge\frac{1}{4}\left(a^2+b^2+c^2\right)\)
Cho a,b,c>0. CMR:
\(\frac{a^4}{b+c}+\frac{b^4}{c+a}+\frac{c^4}{a+b}\ge\frac{a^3+b^3+c^3}{2}\)
\(\frac{a^4}{b+c}+\frac{b^4}{c+a}+\frac{c^4}{a+b}=\frac{a^6}{a^2b+a^2c}+\frac{b^6}{b^2a+b^2c}+\frac{c^6}{c^2a+c^2b}\ge\frac{\left(a^3+b^3+c^3\right)^2}{ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)}\ge\frac{\left(a^3+b^3+c^3\right)^2}{2\left(a^3+b^3+c^3\right)}=\frac{a^3+b^3+c^3}{2}\)
Đúng 0
Bình luận (0)
Với a,b > 0 . CMR:
\(\sqrt[3]{\frac{a^3+b^3}{2}}\le\sqrt[4]{\frac{a^4+b^4}{2}}\)
Dấu "=" ko xảy ra ???
\(\sqrt[3]{\frac{a^3+b^3}{2}}\le\sqrt[3]{\frac{\left(a+b\right)^3}{2}}< \sqrt[3]{\frac{\left(a+b\right)^3}{8}}=\frac{a+b}{2}\)
\(\sqrt[4]{\frac{a^4+b^4}{2}}\ge\sqrt[4]{\frac{\frac{\left(a^2+b^2\right)^2}{2}}{2}}\ge\sqrt[4]{\frac{\left[\frac{\left(a+b\right)^2}{2}\right]^2}{4}}=\sqrt[4]{\frac{\left(a+b\right)^4}{16}}=\frac{a+b}{2}\)
\(VT< VP\)
Đúng 0
Bình luận (0)
Dấu "=" không xảy ra ?!?
\(\sqrt[3]{\frac{a^3+b^3}{2}}\le\frac{a^3+b^3}{2}+1+1=\frac{a^3+b^3+4}{2}\) (theo cô si)
Mặt khác: \(VP>\sqrt[4]{\frac{\frac{\left(a^3+b^3+4\right)^2}{2}}{2}}\ge\sqrt[4]{\frac{\left[\frac{\left(a^3+b^3+4\right)^2}{2}\right]^2}{4}}\)
\(=\sqrt[4]{\frac{\left(a^3+b^3+4\right)^4}{16}}=\frac{a^3+b^3+4}{2}\ge VT\)
Vậy \(VP>VT\)
Đúng 0
Bình luận (0)
\(\sqrt[4]{\frac{a^4+b^4}{2}}=\sqrt[12]{\frac{\left(\frac{a^6}{a^2}+\frac{b^6}{b^2}\right)^3}{8}}\ge\sqrt[12]{\frac{\left(a^3+b^3\right)^6}{8\left(a^2+b^2\right)^3}}\ge\sqrt[12]{\frac{\frac{\left(a^3+b^3\right)^4\left(a^2+b^2\right)^4}{\left(a+b\right)^2}}{8\left(a^2+b^2\right)^3}}\)
\(=\sqrt[12]{\frac{\left(a^3+b^3\right)^4\left(a^2+b^2\right)}{8\left(a+b\right)^2}}\ge\sqrt[12]{\frac{\frac{\left(a^3+b^3\right)^4\left(a+b\right)^2}{2}}{8\left(a+b\right)^2}}=\sqrt[3]{\frac{a^3+b^3}{2}}\)
dấu "=" xay ra khi a=b=c
Cho a,b,c>0. CMR: \(\frac{a^4}{\left(a+b\right)\left(a^2+b^2\right)}+\frac{b^4}{\left(b+c\right)\left(b^2+c^2\right)}+\frac{c^4}{\left(c+a\right)\left(c^2+a^2\right)}\ge\frac{a+b+c}{4}\)