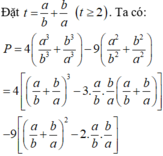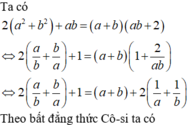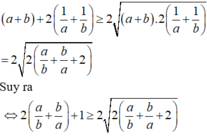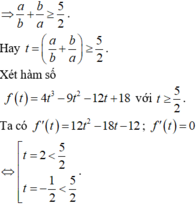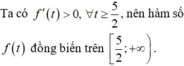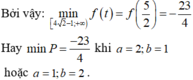Các câu hỏi tương tự
Cho a,b
∈
ℝ
; a,b 0 thỏa mãn . Giá trị nhỏ nhất của biểu thức bằng A.
-
10
B.
-
21
4
C.
-
23
4
D.
23
4
Đọc tiếp
Cho a,b
∈
ℝ
; a,b > 0 thỏa mãn 
. Giá trị nhỏ nhất của biểu thức 
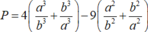bằng
A. - 10
B. - 21 4
C. - 23 4
D. 23 4
cho ba số thực dương a,b,c thỏa mãn \(a^2+b^2+c^2=1\). Tìm giá trị nhỏ nhất của biểu thức \(P=\dfrac{a^3}{2b+3c}+\dfrac{b^3}{2c+3a}+\dfrac{c^3}{2a+3b}\)
cho các số thực dương a,b,c thỏa mãn a+b+c=ab+bc+ac. Tìm giá trị nhỏ nhất của biểu thức \(P=\frac{a^2}{a^2+3bc}+\frac{b^2}{b^2+3ac}+\frac{c^2}{c^2+3ab}+\sqrt{a+b+c}\)
cho ba số thực dương a,b,c thỏa mãn \(a^2+b^2+c^2=1\). Tìm giá trị nhỏ nhất của biểu thức \(P=\dfrac{a^3}{2b+3c}+\dfrac{b^3}{2c+3a}+\dfrac{c^3}{2a+3b}\)
cho 3 số thực dương a,b,c. Tìm giá trị nhỏ nhất của:
\(\)\(\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}+\dfrac{4}{\sqrt{a^2+b^2+c^2+1}}\)
Cho a, b là các số thực thuộc khoảng
0
;
π
2
và thỏa mãn điều kiện
c
o
t
a
-
tan
π
2
-
b
a
-
b
.Tính giá trị của biểu thức
P
3...
Đọc tiếp
Cho a, b là các số thực thuộc khoảng 0 ; π 2 và thỏa mãn điều kiện c o t a - tan π 2 - b = a - b .Tính giá trị của biểu thức P = 3 a + 7 b a + b
A. P=5
B. P=2
C. P=4
D. P=6
Cho các số dương a, b, c thỏa mãn a,b,c Giá trị lớn nhất của biểu thức Pcosb+cosc-
4
sin
3
a
2
là A.
4
6
B.
2
3
6
C.
4
3...
Đọc tiếp
Cho các số dương a, b, c thỏa mãn a,b,c Giá trị lớn nhất của biểu thức P=cosb+cosc- 4 sin 3 a 2 là
A. 4 6
B. 2 3 6
C. 4 3 6
D. 1 6
Với a,b 0 thỏa mãn điều kiện a + b +ab 1, giá trị nhỏ nhất của
P
a
4
+
b
4
bằng. A. B. C. D.
Đọc tiếp
Với a,b > 0 thỏa mãn điều kiện a + b +ab = 1, giá trị nhỏ nhất của P = a 4 + b 4 bằng.
A. 
B. 
C. 
D. 
Cho a, b, c là các số thực thuộc đoạn [1;2] thỏa mãn . Khi biểu thức đạt giá trị lớn nhất thì giá trị của tổng a+b+c là A. 3 B.
3
.
2
1
3
3
C. 4 D. 6
Đọc tiếp
Cho a, b, c là các số thực thuộc đoạn [1;2] thỏa mãn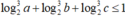 
. Khi biểu thức 
đạt giá trị lớn nhất thì giá trị của tổng a+b+c là
A. 3
B. 3 . 2 1 3 3
C. 4
D. 6