Bài 1: Cho hàm số\(y=x\sqrt{m-1}-\dfrac{3}{2}\).Tìm giá trị của m sao cho hàm số trên là hàm số bậc nhất
Bài 2: Với giá trị nào của k thì:
a)Hàm số \(y=\left(k^2-5k-6\right)x-13\) đồng biến?
b)Hàm số \(y=\left(2k^2+3k-2\right)x+3\) nghịch biến?
Bài 3: Cho hai hàm số bậc nhất y = 2x + k và y = (2m + 1)x + 2k - 3. Tìm điều kiện đối với m và k để hai đồ thị hàm số là:
a)Hai đường thẳng cắt nhau
b)Hai đường thẳng song song với nhau
c)Hai đường thẳng trùng nhau
Bài 4: Cho đường thẳng (d): y = (m - 3)x + 1 - m. Xác định m trong các trường hợp sau đây:
a) (d) cắt trục Ox tại điểm A có hoành độ x = 2
b) (d) cắt trục tung Ox tại điểm B có tung độ y = -3
c) (d) đi qua điểm C(-1 ; 4)
Cho hàm số: \(y=f\left(x\right)=\left(m-1\right)\left(m+2\right)x^2-3mx-4\)
a) Với giá trị nào của m thì hàm số trên là hàm số bậc nhất?
b) Với những giá trị m mà hàm số là bậc nhất thì nó đồng biến, nghịch biến?
Với giá trị nào của m thì hàm số y = \(\dfrac{m}{2}\)x-1 đồng biến ?
Hàm đồng biến khi \(\dfrac{m}{2}>0\Rightarrow m>0\)
Với giá trị nào của m thì hàm số sau đây là hàm số bậc nhất
a, y=\(\sqrt{m-3}\times x+\dfrac{2}{3}\)
b, y= \(\dfrac{\sqrt{m}+\sqrt{5}}{\sqrt{m}-\sqrt{5}}\times x+2010\)
với giá trị nào của m thì hàm số ở ý a là hàm số đồng biến. Với gtri nào của m thì hàm số ở ý b là hàm nghịch biến
a) Ta có: \(y=\sqrt{m-3}\cdot x+\dfrac{2}{3}\left(m\ge3\right)\)
Để đây là hàm số bậc nhất thì: \(\sqrt{m-3}\ne0\Leftrightarrow m=3\)
Do: \(\sqrt{m-3}\ge0\forall m\ge3\)
Nên với \(m\ge3\) thì y đồng biến trên R
b) Ta có: \(y=\dfrac{\sqrt{m}+\sqrt{5}}{\sqrt{m}-\sqrt{5}}\cdot x+2010\left(m\ge0;m\ne5\right)\)
Để đây là hàm số bậc nhất thì: \(\sqrt{m}-\sqrt{5}\ne0\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\m\ne5\end{matrix}\right.\)
Do \(\sqrt{m}+\sqrt{5}>0\Rightarrow\sqrt{m}-\sqrt{5}< 0\Leftrightarrow m< 5\)
Vậy với 0 ≤ m < 5 thì y nghịch biến trên R
a) Để hàm số là hàm số bậc nhất thì:
√(m - 3) > 0
⇔ m - 3 > 0
⇔ m > 3
Vậy với m > 3 thì hàm số đã cho là hàm bậc nhất
b) Để hàm số là hàm bậc nhất thì √m - √5 ≠ 0 và m ≥ 0
⇔ √m ≠ √5
⇔ m ≠ 5
Vậy m ≠ 5 và m ≥ 0 thì hàm số đã cho làm hàm số bậc nhất
*) Để hàm số ở câu a là hàm đồng biến thì m > 3
*) Để hàm số ở câu b là hàm nghịch biến thì √m < √5
⇔ 0 \(\le\) m < 5
Vậy 0 \(\le\) m < 5 thì hàm số ở câu b là hàm số nghịch biến
cho 2 hàm số y=\(\dfrac{m-1}{m+1}\)x +m+2 (1)
a, với giá trị nào thì hàm số (1) là hàm số bậc nhất
b, với giá trị nào thì hàm số (1) là hàm số đồng biến
c, với giá trị nào của m thì đồ thị hàm số (1) đi qua điểm A(1;2)
\(a,\Leftrightarrow\dfrac{m-1}{m+1}\ne0\Leftrightarrow m\ne\pm1\\ b,\Leftrightarrow\dfrac{m-1}{m+1}>0\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\\ c,\Leftrightarrow\dfrac{m-1}{m+1}+m+2=2\\ \Leftrightarrow\dfrac{m-1+m^2+m}{m+1}=0\\ \Leftrightarrow m^2+2m-1=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-1+\sqrt{2}\\m=-1-\sqrt{2}\end{matrix}\right.\)
a.với giá trị nào của m thì hàm số y=(m+2)x-3 đồng biến trên tập xác định
b.với giá trị nào của k hàm số y=(3-k)x+2 nghịch biến trên R
c.trong mặt phẳng tọa độ Oxy tìm m để đường thẳng (d):y=(\(m^2\)-1)x+1
song song với đường thẳng (d') y=3x+m-1
Cho hàm số bậc nhất: \(y=\left(\sqrt{m^2-4m+4}-1\right)x+3\)
a, Với giá trị nào của m thì hàm số y đồng biến?
b, Với giá trị nào của m thì hàm số y nghịch biến?
Với giá trị nào của m thì hàm số:
a) y = f(x) = (m-1)x +m2 -3 đồng biến trên R
b) y = f (x) = -x2 + (m-1)x+2 nghịch biến trên (1;2)
cho hàm số: y = (m-2)x + m+1 (1)
a) với giá trị nào của m thì hs (1) là hàm số bậc nhất
b) với giá trị nào của m thì hs (1) đồng biến
c) vẽ đồ thị hàm số m =1
d) với giá trị nào của m thì đồ thị hàm số (1) đi qua A(2;1)
e) với giá trị nào của m thì đồ thị hàm số (1) song song với y = 3x+2
f) với giá trị nào của m thì đồ thị hàm số (1) tạo với trục Ox một góc tù?
g) với giá trị nào của m thì đồ thị hàm số (1) cắt đường thẳng y = 5x+6 tại trục tung
h) với m =3 tính góc tạo thành bởi đồ thị hàm số với trục hoành và tính khoảng cách từ gốc tọa độ đến đường thẳng
h: Khi m=3 thì \(y=\left(3-2\right)x+3+1=x+4\)
Gọi \(\alpha\) là góc tạo bởi đồ thị hàm số y=x+4 với trục Ox
\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
y=x+4
=>x-y+4=0
Khoảng cách từ O(0;0) đến đường thẳng x-y+4=0 là:
\(\dfrac{\left|0\cdot1+0\cdot\left(-1\right)+4\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{4}{\sqrt{2}}=2\sqrt{2}\)
cho hàm số: y = (m-2)x + m+1 (1)
a) với giá trị nào của m thì hs (1) là hàm số bậc nhất
b) với giá trị nào của m thì hs (1) đồng biến
c) vẽ đồ thị hàm số m =1
d) với giá trị nào của m thì đồ thị hàm số (1) đi qua A(2;1)
e) với giá trị nào của m thì đồ thị hàm số (1) song song với y = 3x+2
f) với giá trị nào của m thì đồ thị hàm số (1) tạo với trục Ox một góc tù?
g) với giá trị nào của m thì đồ thị hàm số (1) cắt đường thẳng y = 5x+6 tại trục tung
h) với m =3 tính góc tạo thành bởi đồ thị hàm số với trục hoành và tính khoảng cách từ gốc tọa độ đến đường thẳng
a: Để (1) là hàm số bậc nhất thì \(m-2\ne0\)
=>\(m\ne2\)
b: Để (1) đồng biến thì m-2>0
=>m>2
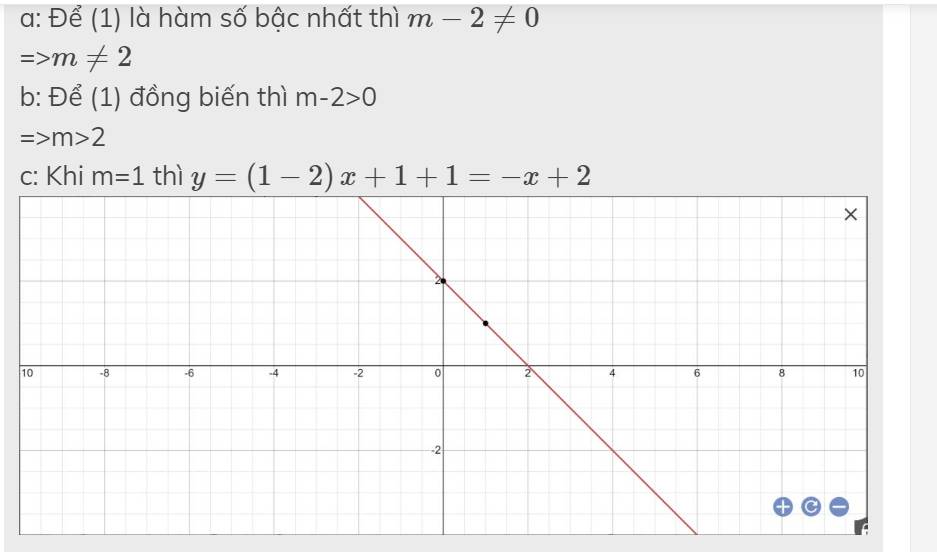
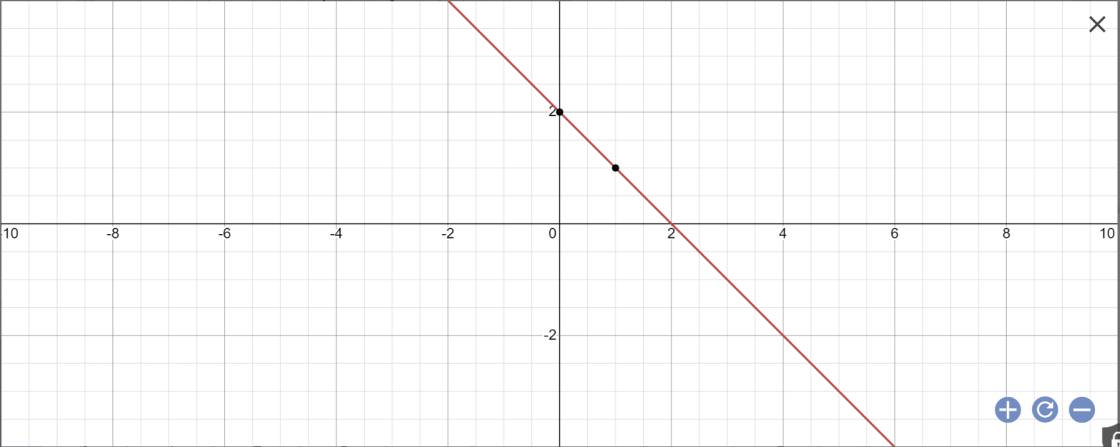
c: Khi m=1 thì \(y=\left(1-2\right)x+1+1=-x+2\)
d: Thay x=2 và y=1 vào (1), ta được:
\(2\left(m-2\right)+m+1=1\)
=>2m-4+m=0
=>3m-4=0
=>3m=4
=>\(m=\dfrac{4}{3}\)
e: Để (1)//y=3x+2 thì \(\left\{{}\begin{matrix}m-2=3\\m+1< >2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=3\\m< >1\end{matrix}\right.\)
=>m=3
f: Để (1) tạo với trục Ox một góc tù thì m-2<0
=>m<2
g: Thay x=0 vào y=5x+6, ta được:
\(y=5\cdot0+6=6\)
Thay x=0 và y=6 vào (1), ta được:
\(0\left(m-2\right)+m+1=6\)
=>m+1=6
=>m=5
