câu này dễ.đầu óc phải linh hoat lên chứ cậu

Ta có : A=\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{9^2}\)

\(\Rightarrow A=\dfrac{1}{2.2}+\dfrac{1}{3.3}+\dfrac{1}{4.4}+...+\dfrac{1}{9.9}\)

^{\(\Rightarrow A=\dfrac{1}{2.2}+\dfrac{1}{3.3}+\dfrac{1}{4.4}+...+\dfrac{1}{9.9}\)}<\(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{8.9}\)

\(\Rightarrow A< \dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{8}-\dfrac{1}{9}\)

\(\Rightarrow A< \dfrac{1}{1}-\dfrac{1}{9}\)

\(\Rightarrow A< \dfrac{9}{9}-\dfrac{1}{9}\)

\(\Rightarrow A< \dfrac{8}{9}\) (1)

\(\Rightarrow A=\dfrac{1}{2.2}+\dfrac{1}{3.3}+\dfrac{1}{4.4}+...+\dfrac{1}{9.9}\)>\(\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{9.10}\)

\(\Rightarrow A>\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{9}-\dfrac{1}{10}\)

\(\Rightarrow A>\dfrac{1}{2}-\dfrac{1}{10}\)

\(\Rightarrow A>\dfrac{5}{10}-\dfrac{1}{10}\)

\(\Rightarrow A>\dfrac{4}{10}\)

\(\Rightarrow A>\dfrac{2}{5}\) (2)

Từ (1) và (2)\(\Rightarrow\dfrac{2}{5}< A< \dfrac{8}{9}\)

Vì \(\dfrac{1}{11}>\dfrac{1}{18}>\dfrac{1}{21}>\dfrac{1}{24}>\dfrac{1}{27}>\dfrac{1}{29}\)

\(\Rightarrow\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}>\dfrac{1}{4}+\dfrac{1}{11}+\dfrac{1}{18}+\dfrac{1}{21}+\dfrac{1}{24}+\dfrac{1}{27}+\dfrac{1}{29}\)\(\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}=\dfrac{1}{11}.7=\dfrac{7}{11}\)

Ta có:

\(\dfrac{7}{11}=\dfrac{7.5}{11.5}=\dfrac{35}{55};\dfrac{4}{5}=\dfrac{4.11}{5.11}=\dfrac{44}{55}\)

\(Vì\) \(\dfrac{44}{55}>\dfrac{35}{55}\)

\(\Rightarrow\dfrac{4}{5}>\dfrac{7}{11}\)

\(\Rightarrow\dfrac{1}{4}+\dfrac{1}{11}+\dfrac{1}{18}+\dfrac{1}{21}+\dfrac{1}{24}+\dfrac{1}{27}+\dfrac{1}{29}< \dfrac{4}{5}\left(đpcm\right)\)

Ta thấy :

\(\dfrac{1}{4}+\dfrac{1}{11}< \dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{2}=1-\dfrac{1}{2}\)

\(\dfrac{1}{18}+\dfrac{1}{21}< \dfrac{1}{12}+\dfrac{1}{12}=\dfrac{1}{6}=\dfrac{1}{2}-\dfrac{1}{3}\)

\(\dfrac{1}{24}+\dfrac{1}{27}< \dfrac{1}{24}+\dfrac{1}{24}=\dfrac{1}{12}=\dfrac{1}{3}-\dfrac{1}{4}\)

\(\dfrac{1}{29}< \dfrac{1}{20}=\dfrac{1}{4}-\dfrac{1}{5}\)

\(\Rightarrow\dfrac{1}{4}+\dfrac{1}{11}+\dfrac{1}{18}+\dfrac{1}{21}+\dfrac{1}{24}+\dfrac{1}{27}+\dfrac{1}{29}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}\)

\(\Rightarrow\dfrac{1}{4}+\dfrac{1}{11}+\dfrac{1}{18}+\dfrac{1}{21}+\dfrac{1}{24}+\dfrac{1}{27}+\dfrac{1}{29}< 1-\dfrac{1}{5}=\dfrac{4}{5}\)

\(\Rightarrow dpcm\)

\(B=\dfrac{2016}{1}+\dfrac{2015}{2}+\dfrac{2014}{3}+...+\dfrac{3}{2014}+\dfrac{2}{2015}+\dfrac{1}{2016}\)

\(B=2016+\dfrac{2015}{2}+\dfrac{2014}{3}+....+\dfrac{3}{2014}+\dfrac{2}{2015}+\dfrac{1}{2016}\)

\(B=1+\left(\dfrac{2015}{2}+1\right)+\left(\dfrac{2014}{3}+1\right)+...+\left(\dfrac{3}{2014}+1\right)+\left(\dfrac{2}{2015}+1\right)+\left(\dfrac{1}{2016}+1\right)\)

\(B=\dfrac{2017}{2017}+\dfrac{2017}{2}+\dfrac{2017}{3}+....+\dfrac{2017}{2014}+\dfrac{2017}{2015}+\dfrac{2017}{2016}\)

\(B=2017\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2014}+\dfrac{1}{2015}+\dfrac{1}{2016}+\dfrac{1}{2017}\right)\)

\(\dfrac{B}{A}=\dfrac{2017\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2014}+\dfrac{1}{2015}+\dfrac{1}{2016}+\dfrac{1}{2017}\right)}{\dfrac{1}{2}+\dfrac{1}{3}+....+\dfrac{1}{2014}+\dfrac{1}{2015}+\dfrac{1}{2016}+\dfrac{1}{2017}}=2017\)

\(\dfrac{B}{A}=\dfrac{\dfrac{2016}{1}+\dfrac{2015}{2}+\dfrac{2014}{3}+...+\dfrac{3}{2014}+\dfrac{2}{2015}+\dfrac{1}{2016}}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+...+\dfrac{1}{2016}+\dfrac{1}{2017}}\)

\(=\dfrac{1+\left(\dfrac{2015}{2}+1\right)+\left(\dfrac{2014}{3}+1\right)+...+\left(\dfrac{2}{2015}+1\right)+\left(\dfrac{1}{2016}+1\right)}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+...+\dfrac{1}{2016}+\dfrac{1}{2017}}\)

\(=\dfrac{\dfrac{2017}{2017}+\left(\dfrac{2015}{2}+\dfrac{2}{2}\right)+\left(\dfrac{2014}{3}+\dfrac{3}{3}\right)+...+\left(\dfrac{1}{2016}+\dfrac{2016}{2016}\right)}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2016}+\dfrac{1}{2017}}\)
\(=\dfrac{2017\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2016}+\dfrac{1}{2017}\right)}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2016}+\dfrac{1}{2017}}\)

\(=2017\)

Vậy \(\dfrac{B}{A}=2017\)

Đặt \(A=\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{2014^2}\)

\(A>\dfrac{1}{5^2}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+...+\dfrac{1}{2014.2015}\)

\(A>\dfrac{1}{5^2}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+...+\dfrac{1}{2014}-\dfrac{1}{2015}\)

\(A>\dfrac{1}{5^2}+\dfrac{1}{6}-\dfrac{1}{2015}\)

\(A>\dfrac{1}{5^2}+\dfrac{1}{6}-\dfrac{1}{150}=\dfrac{1}{5}\) (đpcm)

Chữ hơi xấu thông kẻm :>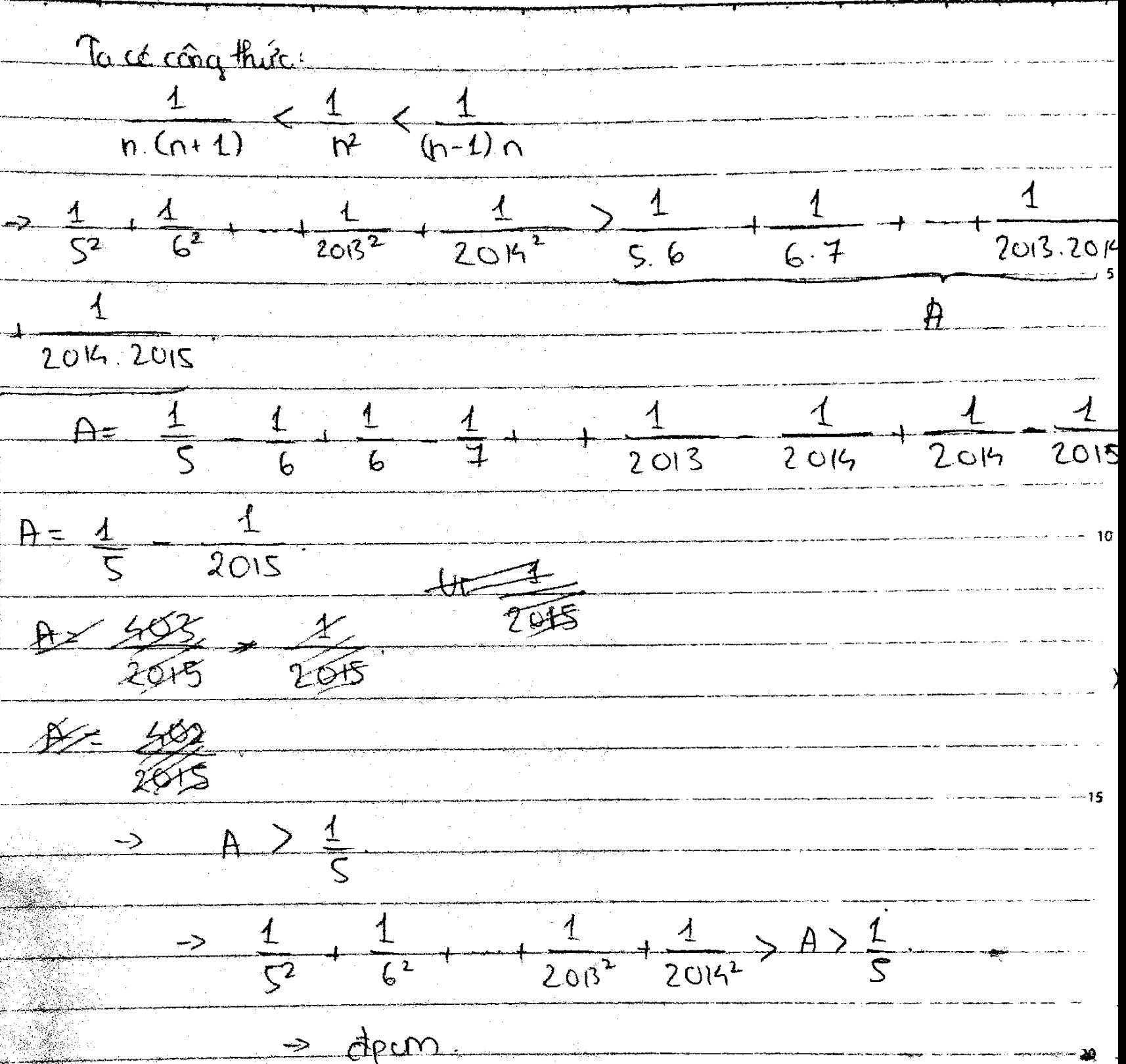

Vội qá nên gạch xóa nhiều :>

\(A=\dfrac{1}{5}+\dfrac{1}{5^2}+...+\dfrac{1}{5^{2015}}\)

\(\Rightarrow5A=1+\dfrac{1}{5}+...+\dfrac{1}{5^{2014}}\)

\(\Rightarrow5A-A=\left(1+\dfrac{1}{5}+...+\dfrac{1}{5^{2014}}\right)-\left(\dfrac{1}{5}+\dfrac{1}{5^2}+...+\dfrac{1}{5^{2015}}\right)\)

\(\Rightarrow4A=1-\dfrac{1}{5^{2015}}\)

\(\Rightarrow A=\dfrac{1}{4}-\dfrac{1}{5^{2015}.4}< \dfrac{1}{4}\)

\(\Rightarrowđpcm\)

\(A=\dfrac{1}{5}+\dfrac{1}{5^2}+\dfrac{1}{5^3}+...+\dfrac{1}{5^{2014}}+\dfrac{1}{5^{2015}}\)

\(\Rightarrow5A=5\left(\dfrac{1}{5}+\dfrac{1}{5^2}+\dfrac{1}{5^3}+...+\dfrac{1}{5^{2014}}+\dfrac{1}{5^{2015}}\right)\)

\(\Rightarrow5A=1+\dfrac{1}{5}+\dfrac{1}{5^2}+...+\dfrac{1}{5^{2013}}+\dfrac{1}{5^{2014}}\)

\(\Rightarrow5A-A=\left(1+\dfrac{1}{5}+\dfrac{1}{5^2}+...+\dfrac{1}{5^{2013}}+\dfrac{1}{5^{2014}}\right)-\left(\dfrac{1}{5}+\dfrac{1}{5^2}+\dfrac{1}{5^3}+...+\dfrac{1}{5^{2014}}+\dfrac{1}{5^{2015}}\right)\)

\(\Rightarrow4A=1-\dfrac{1}{5^{2015}}\)

\(\Rightarrow A=\dfrac{1}{4}-\dfrac{1}{5^{2015}.4}\)

\(\Rightarrow A< \dfrac{1}{4}\)

\(A=\dfrac{\left(3+\dfrac{2}{15}+\dfrac{1}{5}\right):\dfrac{5}{2}}{\left(5+\dfrac{3}{7}-2-\dfrac{1}{4}\right):\left(4+\dfrac{43}{56}\right)}\)

\(=\dfrac{\dfrac{10}{3}\cdot\dfrac{2}{5}}{\dfrac{89}{28}:\dfrac{267}{56}}=\dfrac{4}{3}:\dfrac{2}{3}=2\)

\(B=\dfrac{\dfrac{6}{5}:\left(\dfrac{6}{5}\cdot\dfrac{5}{4}\right)}{\dfrac{8}{25}+\dfrac{2}{25}}=\dfrac{\dfrac{6}{5}:\dfrac{3}{2}}{\dfrac{2}{5}}=2\)

Do đó: A=B

\(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{9^2}\)

=>\(A< \dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{8\cdot9}\)

=>\(A< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{8}-\dfrac{1}{9}=1-\dfrac{1}{9}=\dfrac{8}{9}\)

\(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{9^2}\)

=>\(A>\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{9\cdot10}\)

=>\(A>\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{9}-\dfrac{1}{10}\)

=>\(A>\dfrac{1}{2}-\dfrac{1}{10}=\dfrac{5}{10}-\dfrac{1}{10}=\dfrac{4}{10}=\dfrac{2}{5}\)

Do đó: \(\dfrac{2}{5}< A< \dfrac{8}{9}\)