Đặt \(A=\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{2014^2}\)
\(A>\dfrac{1}{5^2}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+...+\dfrac{1}{2014.2015}\)
\(A>\dfrac{1}{5^2}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+...+\dfrac{1}{2014}-\dfrac{1}{2015}\)
\(A>\dfrac{1}{5^2}+\dfrac{1}{6}-\dfrac{1}{2015}\)
\(A>\dfrac{1}{5^2}+\dfrac{1}{6}-\dfrac{1}{150}=\dfrac{1}{5}\) (đpcm)
Chữ hơi xấu thông kẻm :>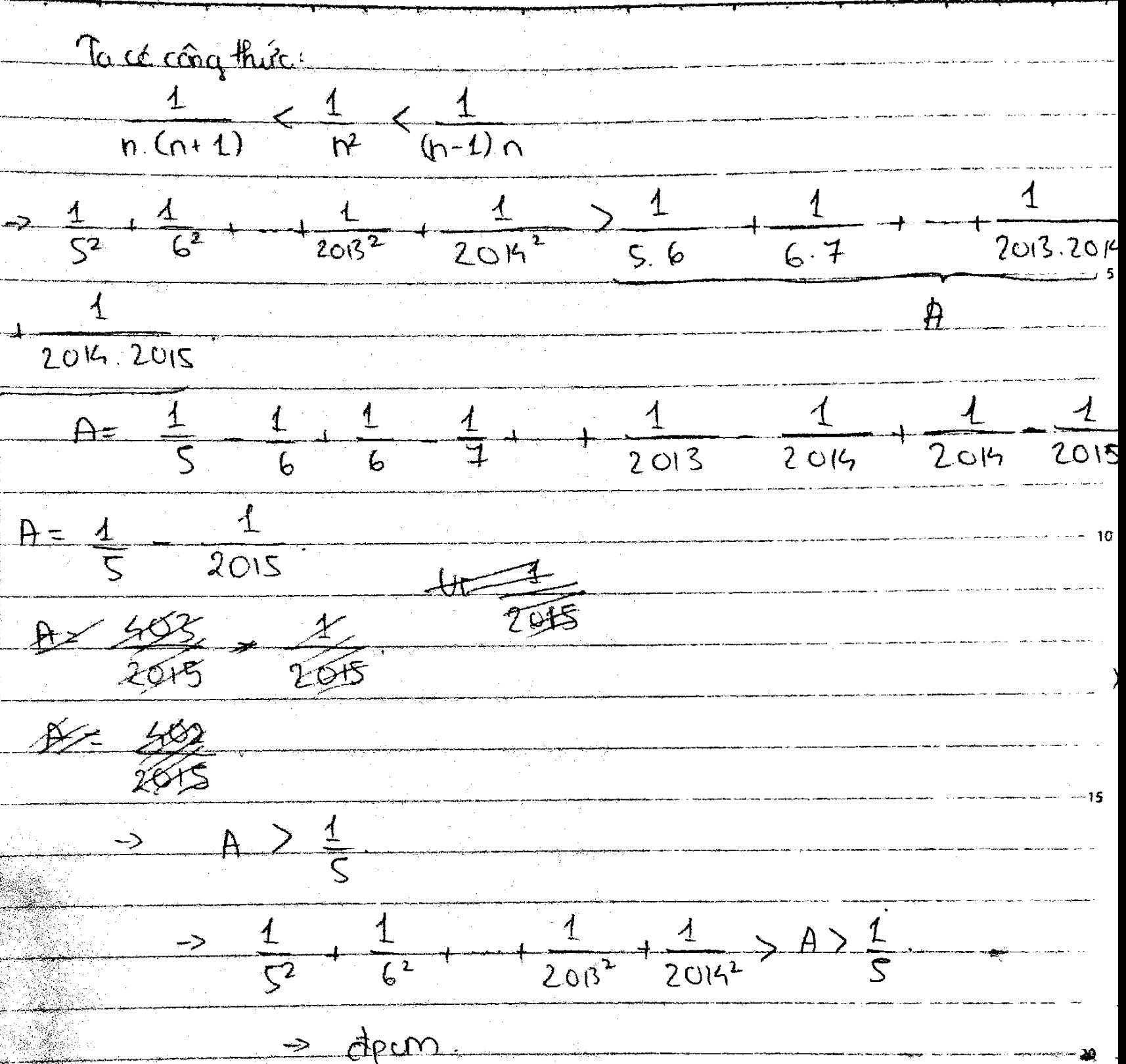
Vội qá nên gạch xóa nhiều :>











