câu này ko có nghĩa đâu nha bạn. nhưng mình thử rùi. pi-2 nha

=>

vậy 2Δπ=1,141592654

\(\pi-2\)

C nhé, dựa vào phương trình sóng tổng quát: x = A cos(wt - 2pi.d/lamda)

M=\(\left(x_1+x_2\right)^2-2x_1.x_2+\left(y_1+y_2\right)^2-2y_1.y_2\)

Áp dụng định lý viettel :( :v )

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}\\x_1x_2=\dfrac{c}{a}\end{matrix}\right.\);\(\left\{{}\begin{matrix}y_1+y_2=-\dfrac{b}{c}\\y_1y_2=\dfrac{a}{c}\end{matrix}\right.\)

\(M=\dfrac{b^2}{a^2}-\dfrac{2c}{a}+\dfrac{b^2}{c^2}-\dfrac{2a}{c}=\dfrac{b^2-4ac}{a^2}+\dfrac{b^2-4ac}{c^2}+2\left(\dfrac{a}{c}+\dfrac{c}{a}\right)\)

\(\ge2\left(\dfrac{a}{c}+\dfrac{c}{a}\right)\ge4\)

Dấu = xảy ra: \(\left\{{}\begin{matrix}a=c\\b^2=4ac\end{matrix}\right.\)\(\Leftrightarrow b^2=4a^2=4c^2\)

@_@ đưa thẳng câu hỏi luôn đi ; nói như zầy chưa nghỉ ra câu trả lời ; chống mặt chết trước rồi

\(\pi-2\)

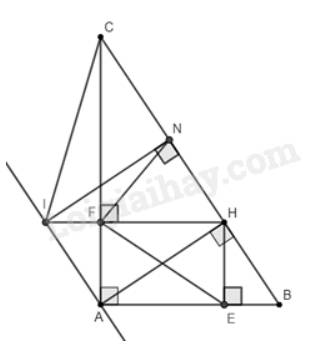
a) Vì \(AH\) là đường cao nên \(\widehat {AHB} = \widehat {AHC} = 90^\circ \)

Xét tam giác \(ABH\) và tam giác \(CBA\) có:

\(\widehat B\) (chung)

\(\widehat {AHB} = \widehat {CAB} = 90^\circ \) (chứng minh trên)

Suy ra, \(\Delta ABH\backsim\Delta CBA\) (g.g).

Do đó, \(\frac{{AB}}{{CB}} = \frac{{BH}}{{AB}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)

Suy ra, \(A{B^2} = BH.BC\) .

b)

-  Vì \(HE\) vuông góc với \(AB\) nên \(\widehat {HEA} = \widehat {HEB} = 90^\circ \)

Xét tam giác \(AHE\) và tam giác \(ABH\) có:

\(\widehat {HAE}\) (chung)

\(\widehat {HEA} = \widehat {AHB} = 90^\circ \) (chứng minh trên)

Suy ra, \(\Delta AHE\backsim\Delta ABH\) (g.g).

Do đó, \(\frac{{AH}}{{AB}} = \frac{{AE}}{{AH}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)

Suy ra, \(A{H^2} = AB.AE\) . (1)

- Vì \(HF\) vuông góc với \(AC\) nên \(\widehat {HFC} = \widehat {HFA} = 90^\circ \)

Xét tam giác \(AHF\) và tam giác \(ACH\) có:

\(\widehat {HAF}\) (chung)

\(\widehat {AFH} = \widehat {AHC} = 90^\circ \) (chứng minh trên)

Suy ra, \(\Delta AHF\backsim\Delta ACH\) (g.g).

Do đó, \(\frac{{AH}}{{AC}} = \frac{{AF}}{{AH}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)

Suy ra, \(A{H^2} = AF.AC\) . (2)

Từ (1) và (2) suy ra, \(AE.AB = AF.AC\) (điều phải chứng minh)

c) Vì \(AE.AB = AF.AC \Rightarrow \frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\).

Xét tam giác \(AFE\) và tam giác \(ABC\) có:

\(\widehat A\) (chung)

\(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\) (chứng minh trên)

Suy ra, \(\Delta AFE\backsim\Delta ABC\) (c.g.c).

d) Vì \(HF\) vuông góc với \(AC\) nên \(CF \bot HI\), do đó, \(\widehat {CFH} = \widehat {CFI} = 90^\circ \).

Vì \(IN \bot CH \Rightarrow \widehat {CBI} = \widehat {HNI} = 90^\circ \).

Xét tam giác \(HFC\) và tam giác \(HNI\) có:

\(\widehat {CHI}\) (chung)

\(\widehat {HFC} = \widehat {HNI} = 90^\circ \) (chứng minh trên)

Suy ra, \(\Delta HFC\backsim\Delta HNI\) (g.g).

Suy ra, \(\frac{{HF}}{{HN}} = \frac{{HC}}{{HI}}\) (hai cặp cạnh tương ứng cùng tỉ lệ)

Do đó, \(\frac{{HF}}{{HC}} = \frac{{HN}}{{HI}}\).

Xét tam giác \(HNF\) và tam giác \(HIC\) có:

\(\widehat {CHI}\) (chung)

\(\frac{{HF}}{{HC}} = \frac{{HN}}{{HI}}\) (chứng minh trên)

Suy ra, \(\Delta HNF\backsim\Delta HIC\) (c.g.c).

Lời giải:

Ta có:

\(A=(x-2y)^2+(x-3)^2+(y-1)^2+3\)

\(=x^2+4y^2-4xy+x^2-6x+9+y^2-2y+1+3\)

\(=2x^2+5y^2-4xy-6x-2y+13\)

\(=2(x^2-2xy+y^2)-6x-2y+3y^2+13\)

\(=2(x-y)^2-2.3(x-y)-8y+3y^2+13\)

\(=2[(x-y)^2-3(x-y)+\frac{3^2}{2^2}]+3(y^2-\frac{8}{3}y+\frac{4^2}{3^2})+\frac{19}{6}\)

\(=2(x-y-\frac{3}{2})^2+3(y-\frac{4}{3})^2+\frac{19}{6}\)

\(\geq 0+0+\frac{19}{6}=\frac{19}{6}\)

Vậy GTNN của $A$ là \(\frac{19}{6}\)

Dấu "=" xảy ra khi \(\left\{\begin{matrix} x-y-\frac{3}{2}=0\\ y-\frac{4}{3}=0\end{matrix}\right.\Leftrightarrow x=\frac{17}{6}; y=\frac{4}{3}\)