\(tanx=-tan\dfrac{\pi}{5}\)

\(\Leftrightarrow tanx=tan\left(-\dfrac{\pi}{5}\right)\)

\(\Leftrightarrow x=-\dfrac{\pi}{5}+k\pi\)

Mình quên mất, nó nằm trong khoảng (π/2; π) nha, mình xin lỗi

1. Không biết yêu cầu đề bài là gì???

2. Biểu thức đề bài ko rõ ràng (ko biết căn thức tới đâu, đâu là tử số đâu là mẫu số).

Bạn cần ghi rõ yêu cầu đề bài, và sử dụng công cụ gõ công thức (kí hiệu khoanh đỏ trên khung soạn thảo) để mọi người đỡ mệt.

1.

\(sin\left(4x-10^0\right)=\dfrac{\sqrt{2}}{2}\)

\(\Leftrightarrow sin\left(4x-10^0\right)=sin45^0\)

\(\Leftrightarrow\left[{}\begin{matrix}4x-10^0=45^0+k360^0\\4x-10^0=135^0+k360^0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}4x=55^0+k360^0\\4x=145^0+k360^0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=13,75^0+k90^0\\x=36,25^0+k90^0\end{matrix}\right.\) (\(k\in Z\))

2.

Đề không đúng

3.

ĐKXĐ: \(\left\{{}\begin{matrix}cos2x\ne0\\cosx\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)

\(tan2x=tanx\)

\(\Rightarrow2x=x+k\pi\)

\(\Rightarrow x=k\pi\)

4.

\(cot\left(x+\dfrac{\pi}{5}\right)=-1\)

\(\Leftrightarrow x+\dfrac{\pi}{5}=-\dfrac{\pi}{4}+k\pi\)

\(\Leftrightarrow x=-\dfrac{9\pi}{20}+k\pi\) (\(k\in Z\))

5.

\(cos3x=sin5x\)

\(\Leftrightarrow sin5x=sin\left(\dfrac{\pi}{2}-3x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}5x=\dfrac{\pi}{2}-3x+k2\pi\\5x=\dfrac{\pi}{2}+3x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}8x=\dfrac{\pi}{2}+k2\pi\\2x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{16}+\dfrac{k\pi}{4}\\x=\dfrac{\pi}{4}+k\pi\end{matrix}\right.\) (\(k\in Z\))

Điều kiện:

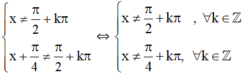
⇔ tan x.(1 - tanx) + tanx + 1 = 1 – tan x.

⇔ tan x - tan2x + 2.tan x = 0

⇔ tan2x - 3tanx = 0

⇔ tanx(tanx - 3) = 0

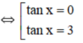
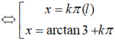
Vậy phương trình đã cho có tập nghiệm là:

{arctan 3+kπ; k ∈ Z }

a.

Tổng là cấp số nhân lùi vô hạn với \(\left\{{}\begin{matrix}u_1=1\\q=-sin^2x\end{matrix}\right.\)

Do đó: \(S=\dfrac{u_1}{1-q}=\dfrac{1}{1+sin^2x}\)

b. Tương tự, tổng cấp số nhân lùi vô hạn với \(\left\{{}\begin{matrix}u_1=1\\q=cos^2x\end{matrix}\right.\)

\(\Rightarrow S=\dfrac{1}{1-cos^2x}=\dfrac{1}{sin^2x}\)

c. Do \(0< x< \dfrac{\pi}{4}\Rightarrow0< tanx< 1\)

Tổng trên vẫn là tổng cấp số nhân lùi vô hạn với \(\left\{{}\begin{matrix}u_1=1\\q=-tanx\end{matrix}\right.\)

\(\Rightarrow S=\dfrac{1}{1+tanx}\)

Bạn ghi đề chính xác ra đi, câu a và câu b đó bạn

Câu a sau \(\frac{4}{cotx}\) còn dấu + nhưng không biết cộng với cái gì

Câu b biểu thức cos đầu tiên là \(cos^2\left(x+\frac{\pi}{3}\right)\) hay \(cos\left(2x+\frac{2\pi}{3}\right)\)

a) Đề thiếu

b)

PT $\Leftrightarrow 1-2\sin^2(x+\frac{\pi}{3})+4\cos (\frac{\pi}{6}-x)-\frac{5}{2}=0$

$\Leftrightarrow 1-2\sin ^2[\frac{\pi}{2}-(\frac{\pi}{6}-x)]+4\cos (\frac{\pi}{6}-x)-\frac{5}{2}=0$

$\Leftrightarrow -2\cos ^2(\frac{\pi}{6}-x)+4\cos (\frac{\pi}{6}-x)-\frac{3}{2}=0$

$\Leftrightarrow -2t^2+4t-\frac{3}{2}=0$ với $t=\cos (\frac{\pi}{6}-x)$

Đến đây bạn giải pt bậc 2 thu được $\cos (\frac{\pi}{6}-x)=\frac{1}{2}$

$\Rightarrow x=2k\pi +\frac{\pi}{2}$ hoặc $x=2k\pi -\frac{\pi}{6}$ với $k$ nguyên

c)

ĐK:.............

PT $\Leftrightarrow 1+\frac{\sin ^2x}{\cos ^2x}-1+\tan x-\sqrt{3}(\tan x+1)=0$

$\Leftrightarrow \tan ^2x+\tan x-\sqrt{3}(\tan x+1)=0$

$\Leftrightarrow \tan ^2x+(1-\sqrt{3})\tan x-\sqrt{3}=0$

$\Rightarrow \tan x=\sqrt{3}$ hoặc $\tan x=-1$

$\Rightarrow x=\pi (k-\frac{1}{4})$ hoặc $x=\pi (k+\frac{1}{3})$ với $k$ nguyên

d)

ĐK:.......

PT $\Leftrightarrow \tan x-\frac{2}{\tan x}+1=0$

$\Leftrightarrow \tan ^2x+\tan x-2=0$

$\Leftrightarrow (\tan x-1)(\tan x+2)=0$

$\Rightarrow \tan x=1$ hoặc $\tan x=-2$

$\Rightarrow x=k\pi +\frac{\pi}{4}$ hoặc $x=k\pi +\tan ^{-2}(-2)$ với $k$ nguyên.

a: tan x(cot^2x-1)

\(=\dfrac{1}{cotx}\left(cot^2x-cotx\cdot tanx\right)\)

=cotx-tanx/cotx=cotx(1-tan^2x)

b: \(tan^2x-sin^2x=\dfrac{sin^2x}{cos^2x}-sin^2x\)

\(=sin^2x\left(\dfrac{1}{cos^2x}-1\right)=sin^2x\cdot\dfrac{sin^2x}{cos^2x}=sin^2x\cdot tan^2x\)

c: \(\dfrac{cos^2x-sin^2x}{cot^2x-tan^2x}=\dfrac{cos^2x-sin^2x}{\dfrac{cos^2x}{sin^2x}-\dfrac{sin^2x}{cos^2x}}\)

\(=\left(cos^2x-sin^2x\right):\dfrac{cos^4x-sin^4x}{sin^2x\cdot cos^2x}\)

\(=\dfrac{sin^2x\cdot cos^2x}{1}=sin^2x\cdot cos^2x\)

=>sin^2x*cos^2x-cos^2x=cos^2x(sin^2x-1)

=-cos^2x*cos^2x=-cos^4x

=>ĐPCM

\(\Leftrightarrow3x-2-2x-3=-1\)

\(\Leftrightarrow x=-1+2+3\)

\(\Leftrightarrow x=4\)

\(\left(3x-2\right)-\left(2x+3\right)=-1\)

\(\Leftrightarrow3x-2-2x-3=-1\)

\(\Leftrightarrow x=4\)

\(1+tanx+tan^2x+tan^3x\)

\(1+\dfrac{sinx}{cosx}+\dfrac{sin^2x}{cos^2x}+\dfrac{sin^3x}{cos^3x}\)

\(=\dfrac{cos^3x+sinx.cos^2x+sin^2x.cosx+sin^3x}{cos^3x}\)

\(=\dfrac{cos^2x.\left(sinx+cosx\right)+sin^2x.\left(sinx+cosx\right)}{cos^3x}\)

\(=\dfrac{\left(sin^2x+cos^2x\right)\left(sinx+cosx\right)}{cos^3x}=\dfrac{sinx+cosx}{cos^3x}\)

\(\dfrac{\sin x+\cos x}{\cos x}.\dfrac{1}{\cos^2x}=\left(\tan x+1\right)\left(\tan^2x+1\right)=\tan^4x+\tan x+\tan^2x+\left(đpcm\right)\)