Điều kiện:
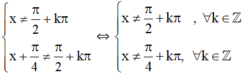
⇔ tan x.(1 - tanx) + tanx + 1 = 1 – tan x.
⇔ tan x - tan2x + 2.tan x = 0
⇔ tan2x - 3tanx = 0
⇔ tanx(tanx - 3) = 0
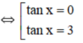
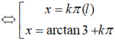
Vậy phương trình đã cho có tập nghiệm là:
{arctan 3+kπ; k ∈ Z }
Điều kiện:
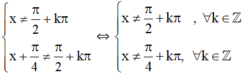
⇔ tan x.(1 - tanx) + tanx + 1 = 1 – tan x.
⇔ tan x - tan2x + 2.tan x = 0
⇔ tan2x - 3tanx = 0
⇔ tanx(tanx - 3) = 0
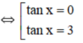
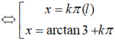
Vậy phương trình đã cho có tập nghiệm là:
{arctan 3+kπ; k ∈ Z }
Số nghiệm thuộc khoảng 0 ; π của phương trình tan x + sin x + tan x - sin x = 3 tan x là
A. 0.
B. 1.
C. 2.
D. 3.
Số nghiệm thuộc khoảng 0 ; π của phương trình. tan x + sin x = tan x - sin x = 3 tan x là
A. 0.
B. 1
C. 2.
D. 3.
Số nghiệm thuộc khoảng 0 ; π của phương trình.
tan x + sin x + tan x - sin x = 3 tan x là
A. 0.
B. 1
C. 2.
D. 3
Phương trình tanx + tan(x + π 3 ) + tan(x + 2 π 3 ) = 3 3 tương đương với phương trình.
A. cot x = 3
B. cot 3x = 3
C. tan x = 3
D. tan 3x = 3
Giải phương trình sau: tanx = -1
Giải phương trình sau: tanx = 1
giải phương trình
a) \(tanx=-1\)
b) \(tan\)(x+20 độ) = tan60 độ
c) \(tan3x=tan\left(x-\dfrac{\pi}{6}\right)\)
d) \(tan\left(5x+\dfrac{\pi}{4}\right)=0\)
e) \(cot\left(2x-\dfrac{\pi}{4}\right)=0\)
giải phương trình
a) \(tanx=1\)
b) \(tanx=tan55\) độ
c) \(tan2x=tan\dfrac{\pi}{5}\)
d) \(tan\left(2x+\dfrac{\pi}{3}\right)\)= 0
e) \(cot\left(x-\dfrac{\pi}{3}\right)=0\)
Phương trình tan( x - π/4) = 0 có nghiệm là:
A. x = π/4 + kπ, k ∈ Z.
B. x = 3π/4 + kπ, k ∈ Z.
C. x = kπ, k ∈ Z.
D. x = k2π, k ∈ Z.