Các câu hỏi tương tự
Cho phương trình cos2x.cosx + sinx.cos3x sin2x.sinx - sin3x.cosx và các họ số thực: I. x
π
4
+ kπ, k ∈ Z. II. x
-
π
2
+ k2π, k ∈ Z. III. x
-
π
14
+
k
2
π
7
, k ∈ Z. ...
Đọc tiếp
Cho phương trình cos2x.cosx + sinx.cos3x = sin2x.sinx - sin3x.cosx và các họ số thực:
I. x = π 4 + kπ, k ∈ Z.
II. x = - π 2 + k2π, k ∈ Z.
III. x = - π 14 + k 2 π 7 , k ∈ Z.
IV. x = π 7 + k 4 π 7 , k ∈ Z.
Chọn trả lời đúng: Nghiệm của phương trình là:
A. I, II
B. I, III
C. II, III
D. II, IV.
Tính đạo hàm của hàm số: y = tan π / 2 – x với x ≠ k π , k ∈ Z
2
cos
3
x
sin
3
x
phương trình đã cho có nghiệm
x
π
4
+
k
π
x...
Đọc tiếp
2 cos 3 x = sin 3 x phương trình đã cho có nghiệm x = π 4 + k π x = a r c t a n + k π k ∈ Z vậy A là:
A.2
B.3
C.4
D.-2
Cho hàm số y sin4xa) Chứng minh rằng sin4(x + kπ/2) sin4x với k ∈ ZTừ đó vẽ đồ thị của hàm sốy sin4x; (C1)y sin4x + 1. (C2)b) Xác định giá trị của m để phương trình: sin4x + 1 m (1)- Có nghiệm- Vô nghiệmc) Viết phương trình tiếp tuyến của (C2) tại điểm có hoành độ
x
0
π
/
24
Đọc tiếp
Cho hàm số y = sin4x
a) Chứng minh rằng sin4(x + kπ/2) = sin4x với k ∈ Z
Từ đó vẽ đồ thị của hàm số
y = sin4x; (C1)
y = sin4x + 1. (C2)
b) Xác định giá trị của m để phương trình: sin4x + 1 = m (1)
- Có nghiệm
- Vô nghiệm
c) Viết phương trình tiếp tuyến của (C2) tại điểm có hoành độ x 0 = π / 24
Cho hàm số
y
cos
2
x
.a) Chứng minh rằng cos
2
x
+
k
π
cos
2
x
với mọi số nguyên k. Từ đó vẽ đồ thị (C) của hàm số
y
cos
2
x
.b) Viết phương...
Đọc tiếp
Cho hàm số y = cos 2 x .
a) Chứng minh rằng cos 2 x + k π = cos 2 x với mọi số nguyên k. Từ đó vẽ đồ thị (C) của hàm số y = cos 2 x .
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π / 3 .
c) Tìm tập xác định của hàm số : z = 1 - cos 2 x 1 + cos 2 2 x
Phương trình sinx-3cosx=0 có nghiệm dạng x = a r c c o t m + k π , k ∈ ℤ thì giá trị m là?
A. -3
B. 1 3
C. 3
D. 5
Tìm lim un với un=\(\sum\limits^n_{k=1}sin^k\alpha\) (α≠\(\dfrac{\pi}{2}\) +kπ, k ϵ Z)
Chứng minh rằng cos2(x + kπ) = cos2x, k ∈ Z. Từ đó vẽ đồ thị hàm số y = cos2x
Từ đồ thị hàm số y = cos2x, hãy vẽ đồ thị hàm số y = |cos2x|
Cho hàm số
f
(
x
)
tan
x
x
;
x
k
h
á...
Đọc tiếp
Cho hàm số f ( x ) = tan x x ; x k h á c 0 ∧ x k h á c π 2 + k π ; k ∈ ℤ 0 ; x = 0 Hàm số y = f(x) liên tục trên các khoảng nào sau đây?
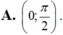
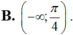
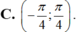
![]()
Tập nghiệm của phương trình -9sinx+6cosx-3sin2x+cos2x= -10 là: x = a π b + k 2 π ( k ∈ Z ) tính giá trị của a2 – b : (biết a, b tối giản)
A.3
B.-2
C.4
D.-1




