Chọn A.
TXĐ: 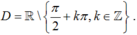 .
.
Với x = 0 ta có f(0) = 0.
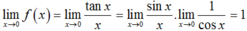 hay
hay ![]() .
.
Vậy hàm số gián đoạn tại x = 0.
Chọn A.
TXĐ: 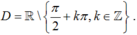 .
.
Với x = 0 ta có f(0) = 0.
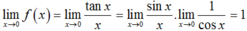 hay
hay ![]() .
.
Vậy hàm số gián đoạn tại x = 0.
Tính đạo hàm của hàm số: y = tan π / 2 – x với x ≠ k π , k ∈ Z
Cho hàm số f(x) = sin3x.
Tính f''(-π/2), f''(0), f''(π/18)
Cho các mệnh đề sau
(I) Hàm số f(x) = sin x x 2 + 1 là hàm số chẵn.
(II) Hàm số f(x) = 3sinx + 4cosx có giá trị lớn nhất là 5.
(III) Hàm số f(x) = tanx tuần hoàn với chu kì 2 π .
(IV) Hàm số f(x) = cosx đồng biến trên khoảng (0; π )
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng?
A. 4
B. 2
C. 3
D. 1
Cho khoảng K, x 0 ∈ K và hàm số y = f(x) xác định trên K \ x 0
Chứng minh rằng nếu lim x → x 0 f ( x ) = + ∞ thì luôn tồn tại ít nhất một số c thuộc sao cho f(c) > 0
Hãy xác định giá trị của x trên đoạn [- π ; 3π/2] để hàm số y = tan x:
a. Nhận giá trị bằng 0
b. Nhận giá trị bằng 1
c. Nhận giá trị dương
d. Nhận giá trị âm
Cho hàm số y = cos 2 x .
a) Chứng minh rằng cos 2 x + k π = cos 2 x với mọi số nguyên k. Từ đó vẽ đồ thị (C) của hàm số y = cos 2 x .
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π / 3 .
c) Tìm tập xác định của hàm số : z = 1 - cos 2 x 1 + cos 2 2 x
Hàm số y = tan ( x / 2 - π / 4 ) có tập xác định là:
A. R\{π/2+k2π, k ∈ Z}.
B. R\{π/2+kπ, k ∈ Z}.
C. R\{3π/2+k2π, k ∈ Z}.
D. R.
Cho hàm số y = sin4x
a) Chứng minh rằng sin4(x + kπ/2) = sin4x với k ∈ Z
Từ đó vẽ đồ thị của hàm số
y = sin4x; (C1)
y = sin4x + 1. (C2)
b) Xác định giá trị của m để phương trình: sin4x + 1 = m (1)
- Có nghiệm
- Vô nghiệm
c) Viết phương trình tiếp tuyến của (C2) tại điểm có hoành độ x 0 = π / 24
Hàm số y = tan(x+ π/5) có phải là hàm số lẻ không?Tại sao?