Tìm GTLN của:
a.y=cosx+1/cos2x, x E (-pi/2;pi/2)
b.y=(sinx)^2017 +|cosx|^2017
Giải các pt sau
a, \(\dfrac{1}{sinx}+\dfrac{1}{cosx}=4sin\left(x+\dfrac{\pi}{4}\right)\)
b, \(2sin\left(2x-\dfrac{\pi}{6}\right)+4sinx+1=0\)
c, \(cos2x+\sqrt{3}sinx+\sqrt{3}sin2x-cosx=2\)
d, \(4sin^2\dfrac{x}{2}-\sqrt{3}cos2x=1+cos^2\left(x-\dfrac{3\pi}{4}\right)\)
24. Tìm GTLN của hàm số: \(y=3\cos\left(x-\dfrac{\pi}{2}\right)+1\)
26. a) Tìm GTLN của hàm số: \(y=\cos2x+\sin2x\)
b) Giải PT: \(\sin x+\sqrt{3}\cos x=1\)
24.
\(cos\left(x-\dfrac{\pi}{2}\right)\le1\Rightarrow y\le3.1+1=4\)
\(y_{max}=4\)
26.
\(y=\sqrt{2}cos\left(2x-\dfrac{\pi}{4}\right)\)
Do \(cos\left(2x-\dfrac{\pi}{4}\right)\le1\Rightarrow y\le\sqrt{2}\)
\(y_{max}=\sqrt{2}\)
b.
\(\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{6}=\dfrac{\pi}{3}+k2\pi\\x-\dfrac{\pi}{6}=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
1) So nghiem phuong trinh \(\dfrac{\left(1+cos2x+sin2x\right)cosx+cos2x}{1+tanx}=cosx\) voi x ∈ (0; \(\dfrac{\Pi}{2}\)) la: (giai ra nua nha)
A. 0 B. 1 C. 2 D. 3
ĐKXĐ: \(\left\{{}\begin{matrix}x\ne\dfrac{\pi}{2}+k\pi\\x\ne-\dfrac{\pi}{4}+k\pi\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{\left(1+2cos^2x-1+2sinx.cosx\right)cosx+cos^2x-sin^2x}{1+\dfrac{sinx}{cosx}}=cosx\)
\(\Leftrightarrow\dfrac{2cos^2x\left(sinx+cosx\right)+\left(sinx+cosx\right)\left(cosx-sinx\right)}{\dfrac{sinx+cosx}{cosx}}=cosx\)
\(\Leftrightarrow\dfrac{cosx\left(sinx+cosx\right)\left(2cos^2x+cosx-sinx\right)}{sinx+cosx}=cosx\)
\(\Rightarrow2cos^2x+cosx-sinx=1\)
\(\Rightarrow cosx-sinx-cos2x=0\)
\(\Rightarrow cosx-sinx-\left(cos^2x-sin^2x\right)=0\)
\(\Rightarrow cosx-sinx-\left(cosx-sinx\right)\left(cosx+sinx\right)=0\)
\(\Rightarrow\left(cosx-sinx\right)\left(1-sinx-cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=cosx\\sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\) \(\Rightarrow x=\dfrac{\pi}{4}\)
Có 1 nghiệm trên khoảng đã cho
tìm m để pt cos2x-(2m-1)cosx-2m=0 x thuộc (-pi/2;pi/2)
\(\Leftrightarrow2cos^2x-1-\left(2m-1\right)cosx-2m=0\)
\(\Leftrightarrow2cos^2x+cosx-1-2m\left(cosx+1\right)=0\)
\(\Leftrightarrow\left(cosx+1\right)\left(2cos-1\right)-2m\left(cosx+1\right)=0\)
\(\Leftrightarrow\left(cosx+1\right)\left(2cosx-2m-1\right)=0\)
\(\Leftrightarrow cosx=\frac{2m+1}{2}\)
Do \(x\in\left(-\frac{\pi}{2};\frac{\pi}{2}\right)\Rightarrow0< cosx\le1\)
\(\Rightarrow0< \frac{2m+1}{2}\le1\Rightarrow-\frac{1}{2}< m\le\frac{1}{2}\)
\(sinx+4cosx=2+sin2x\)
\(\left(1-sin2x\right)\left(sinx+cosx\right)=cos2x\)
\(1+sinx+cosx+sin2x+cos2x=0\)
\(sinx+sin2x+sin3x=1+cosx+cos2x\)
\(sin^22x-cos^28x=sin\left(\dfrac{17\pi}{2}+10x\right)\)
1) hàm số \(y=3sinx\) luôn nhận giá trị trong tập nào
2) cho \(cosx=-\dfrac{2}{3}\), \(cos2x\) bằng
3) cho \(cosx=-\dfrac{3}{5}\), \(\dfrac{\pi}{2}< x< \pi\) thì \(sin2x\)
Tìm GTLN và GTNN của y=cos2x+cosx
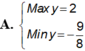
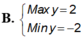

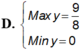
1. Cho sinx = \(\dfrac{2}{3}\) , x ∈ (0,\(\dfrac{\Pi}{2}\))
Tính cosx, tanx , sin (x+\(\dfrac{\Pi}{4}\))
2. Cho cos = \(\dfrac{1}{4}\) . Tính sinx, cos2x
3. Cho tanx = 2 . Tính cosx, sinx
x ∈ (0,\(\dfrac{\Pi}{2}\))
4. Rút gọn a) A = cos2x - 2cos2x + sinx +1
b) B = \(\dfrac{cos3x+cos2x+cosx}{cos2x}\)
1.
\(0< x< \dfrac{\pi}{2}\Rightarrow cosx>0\)
\(\Rightarrow cosx=\sqrt{1-sin^2x}=\dfrac{\sqrt{5}}{3}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{2}{\sqrt{5}}\)
\(sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\left(sinx+cosx\right)=\dfrac{\sqrt{10}+2\sqrt{2}}{6}\)
2.
Đề bài thiếu, cos?x
Và x thuộc khoảng nào?
3.
\(x\in\left(0;\dfrac{\pi}{2}\right)\Rightarrow sinx;cosx>0\)
\(\dfrac{1}{cos^2x}=1+tan^2x=5\Rightarrow cos^2x=\dfrac{1}{5}\Rightarrow cosx=\dfrac{\sqrt{5}}{5}\)
\(sinx=cosx.tanx=\dfrac{2\sqrt{5}}{5}\)
4.
\(A=\left(2cos^2x-1\right)-2cos^2x+sinx+1=sinx\)
\(B=\dfrac{cos3x+cosx+cos2x}{cos2x}=\dfrac{2cos2x.cosx+cos2x}{cos2x}=\dfrac{cos2x\left(2cosx+1\right)}{cos2x}=2cosx+1\)
Giải pt
\(2sin\left(x+\dfrac{\pi}{6}\right)+sinx+2cosx=3\)
\(\left(sin2x+cos2x\right)cosx+2cos2x-sinx=0\)
\(sin2x-cos2x+3sinx-cosx-1=0\)
1.
\(2sin\left(x+\dfrac{\pi}{6}\right)+sinx+2cosx=3\)
\(\Leftrightarrow\sqrt{3}sinx+cosx+sinx+2cosx=3\)
\(\Leftrightarrow\left(\sqrt{3}+1\right)sinx+3cosx=3\)
\(\Leftrightarrow\sqrt{13+2\sqrt{3}}\left[\dfrac{\sqrt{3}+1}{\sqrt{13+2\sqrt{3}}}sinx+\dfrac{3}{\sqrt{13+2\sqrt{3}}}cosx\right]=3\)
Đặt \(\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)
\(pt\Leftrightarrow\sqrt{13+2\sqrt{3}}sin\left(x+\alpha\right)=3\)
\(\Leftrightarrow sin\left(x+\alpha\right)=\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\\x+\alpha=\pi-arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)
Vậy phương trình đã cho có nghiệm:
\(x=k2\pi;x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\)
2.
\(\left(sin2x+cos2x\right)cosx+2cos2x-sinx=0\)
\(\Leftrightarrow2sinx.cos^2x+cos2x.cosx+2cos2x-sinx=0\)
\(\Leftrightarrow\left(2cos^2x-1\right)sinx+cos2x.cosx+2cos2x=0\)
\(\Leftrightarrow cos2x.sinx+cos2x.cosx+2cos2x=0\)
\(\Leftrightarrow cos2x.\left(sinx+cosx+2\right)=0\)
\(\Leftrightarrow cos2x=0\)
\(\Leftrightarrow2x=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Vậy phương trình đã cho có nghiệm \(x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)