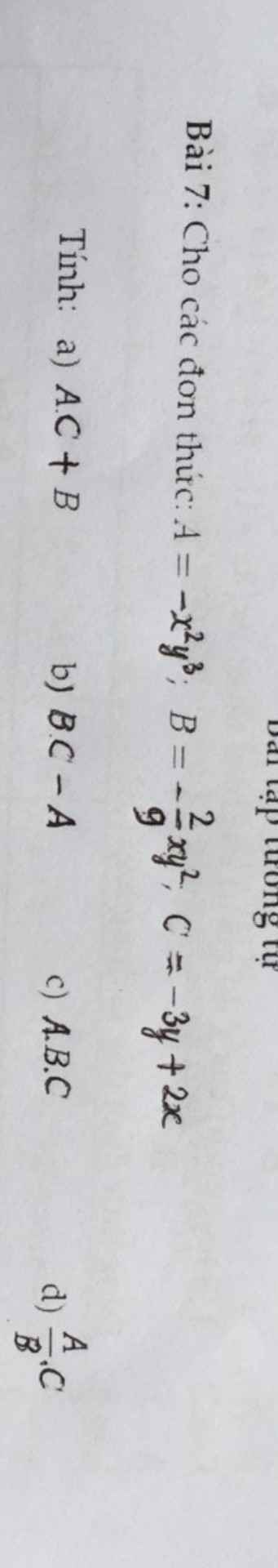
giúp em phần d với
Giúp em phần d) với
chữ xấu vãiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
Giúp em phần d với ạ

a) Để C cõ nghĩa <=> \(\left\{{}\begin{matrix}2x-2\ne0< =>x\ne1\\2-2x^2\ne0< =>x\ne\pm1\end{matrix}\right.\)
b) C = \(\dfrac{x}{2\left(x-1\right)}-\dfrac{x^2+1}{2x^2-2}=\dfrac{x}{2\left(x-1\right)}-\dfrac{x^2+1}{2\left(x-1\right)\left(x+1\right)}\)
= \(\dfrac{x\left(x+1\right)-x^2-1}{2\left(x-1\right)\left(x+1\right)}=\dfrac{x^2+x-x^2-1}{2\left(x+1\right)\left(x-1\right)}=\dfrac{1}{2\left(x+1\right)}\)
c) Để C = \(\dfrac{-1}{2}\)
<=> \(\dfrac{1}{2\left(x+1\right)}=\dfrac{-1}{2}\)
<=> x+ 1 = -1
<=> x = -2 (tm)
d) Để C nguyên
<=> \(\dfrac{1}{2\left(x+1\right)}\) nguyên
<=> 2(x+1) có dạng \(\dfrac{1}{k}\left(k\in Z,k\ne0\right)\)
<=> \(x+1=\dfrac{1}{2k}< =>x=\dfrac{1}{2k}-1\)

Giúp em phần c,d và 37,39 với ạ
Bài 39:
a: Đặt \(\dfrac{5}{x-2}-\dfrac{1}{x+2}+\dfrac{4}{\left(x-2\right)\left(x+2\right)}=0\)
=>5x+10-x+2+4=0
=>4x+16=0
hay x=-4(nhận)
b: Đặt \(\dfrac{-2}{x^2-x+1}+x+1=0\)
\(\Leftrightarrow-2+x^3+1=0\)
\(\Leftrightarrow x^3=1\)
hay x=1(nhận)
Mn giúp em phần d câu 3 đề 1 với ạ , em đang cần gấp , em cảm ơn nhiều 
giúp em với. Xác định các phần tử trong dung dịch các chất sau : a. HNO3 b. HNO2 c. H2CO3 d. CH3COOH
\(a.H^+,NO^-_3\\ b.H^+,NO^-_2\\ c.H^+,CO^{2-}_3\\ d.CH_3COO^-,H^+\)
Hướng dẫn cách giải giúp em với ạ!
E={a;b;c;d;đ,e;ê}
CÓ BAO NHIÊU TẬP CON CÓ 3 PHẦN TỬ TRONG ĐÓ LUÔN CÓ PHẦN TỬ a
Các tập hợp tạo thành được:
\(\left\{a;b;c\right\};\left\{a;b;d\right\};\left\{a;b;đ\right\};\left\{a;b;e\right\};\left\{a;b;\text{ê}\right\};\\ \left\{a;c;d\right\};\left\{a;c;đ\right\};\left\{a;c;e\right\};\left\{a;c;\text{ê}\right\};\left\{a;d;đ\right\};\\ \left\{a;d;e\right\};\left\{a;d;\text{ê}\right\};\left\{a;đ;e\right\};\left\{a;\text{đ};\text{ê}\right\};\left\{a;e;\text{ê}\right\}\)
Có thể tạo thành 15 tập hợp
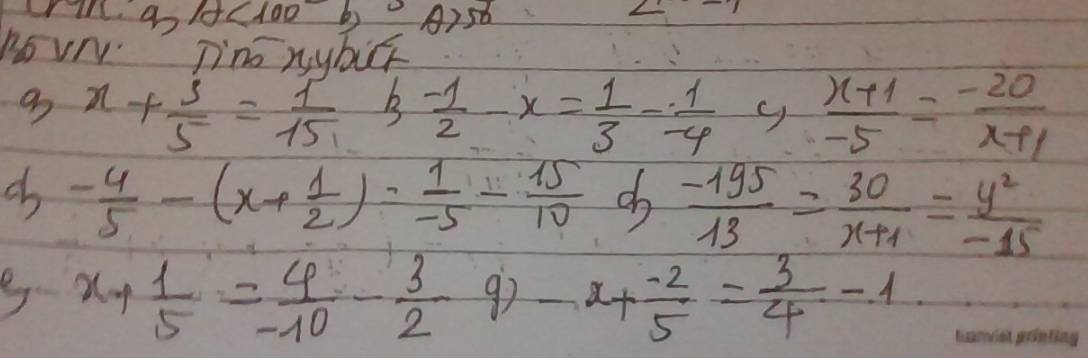
em cần giúp phần BTVN phần c) + d) (2 phần) + e) ạ
c: \(\dfrac{x+1}{-5}=\dfrac{-20}{x+1}\)(Điều kiện: \(x\ne-1\))
=>\(\left(x+1\right)^2=\left(-20\right)\cdot\left(-5\right)=100\)
=>\(\left[{}\begin{matrix}x+1=10\\x+1=-10\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=9\left(nhận\right)\\x=-11\left(nhận\right)\end{matrix}\right.\)
d: \(\dfrac{-4}{5}-\left(x+\dfrac{1}{2}\right)=\dfrac{1}{-5}-\dfrac{15}{10}\)
=>\(\dfrac{-4}{5}-x-\dfrac{1}{2}=\dfrac{-1}{5}-\dfrac{15}{10}\)
=>\(\dfrac{-13}{10}-x=\dfrac{-17}{10}\)
=>\(x=\dfrac{-13}{10}+\dfrac{17}{10}=\dfrac{4}{10}=\dfrac{2}{5}\)
d:
ĐKXĐ: x<>-1
\(-\dfrac{195}{13}=\dfrac{30}{x+1}=\dfrac{y^2}{-15}\)
=>\(\dfrac{30}{x+1}=\dfrac{y^2}{-15}=-15\)
=>\(\left\{{}\begin{matrix}x+1=\dfrac{30}{-15}=-2\\y^2=\left(-15\right)\cdot\left(-15\right)=225\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-3\left(nhận\right)\\y\in\left\{15;-15\right\}\end{matrix}\right.\)
e: \(x+\dfrac{1}{5}=\dfrac{4}{-10}-\dfrac{3}{2}\)
=>\(x+\dfrac{1}{5}=\dfrac{-2}{5}-\dfrac{3}{2}\)
=>\(x=\dfrac{-2}{5}-\dfrac{3}{2}-\dfrac{1}{5}=\dfrac{-3}{2}-\dfrac{3}{5}=\dfrac{-21}{10}\)
c.
\(\dfrac{x+1}{-5}=\dfrac{-20}{x+1}\)
\(\Rightarrow\left(x+1\right)^2=-20.\left(-5\right)\)
\(\Leftrightarrow\left(x+1\right)^2=100\)
\(\Rightarrow x+1=10\) hoặc \(x+1=-10\)
\(\Rightarrow x=9\) hoặc \(x=-11\)
d.
\(-\dfrac{4}{5}-\left(x+\dfrac{1}{2}\right)=\dfrac{1}{-5}-\dfrac{15}{10}\)
\(\Rightarrow-\dfrac{4}{5}-\left(x+\dfrac{1}{2}\right)=-\dfrac{17}{10}\)
\(\Rightarrow x+\dfrac{1}{2}=-\dfrac{4}{5}+\dfrac{17}{10}\)
\(\Rightarrow x+\dfrac{1}{2}=\dfrac{9}{10}\)
\(\Rightarrow x=\dfrac{9}{10}-\dfrac{1}{2}\)
\(\Rightarrow x=\dfrac{2}{5}\)
d.
\(\dfrac{-195}{13}=\dfrac{30}{x+1}=\dfrac{y^2}{-15}\)
\(\Rightarrow-15=\dfrac{30}{x+1}=\dfrac{y^2}{-15}\)
\(\Rightarrow\left\{{}\begin{matrix}x+1=30:\left(-15\right)\\y^2=-15.\left(-15\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x+1=-2\\y^2=15^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-3\\y=\pm15\end{matrix}\right.\)
e.
\(x+\dfrac{1}{5}=\dfrac{4}{-10}-\dfrac{3}{2}\)
\(x+\dfrac{1}{5}=-\dfrac{2}{5}-\dfrac{3}{2}\)
\(x+\dfrac{1}{5}=-\dfrac{19}{10}\)
\(x=-\dfrac{19}{10}-\dfrac{1}{5}\)
\(x=-\dfrac{21}{10}\)
Giúp em phần D
a. Cho đường thẳng (d): y = x + 1 và đường thẳng (d'): y = 2x - 2m - 1.
Tìm m để đường thẳng (d) và (d') cắt nhau tại 1 điểm nằm trong góc phần tư thứ II (em không biết là thứ 11 hay thứ II nữa thầy cô coi giúp em với ạ). (dạ giải rồi làm phước giúp em giải thích luôn câu in đậm em cảm ơn ạ)
b. Cho phương trình: \(x^2+6x+6m-m^2=0\) (với m là tham số). Tìm m để phương trình đã cho có 2 nghiệm \(x_1;x_2\) thỏa mãn:
\(x_1^3-x_2^3+2x_1^2+12x_1+72=0\)
a.
Pt hoành độ giao điểm (d) và (d'):
\(x+1=2x-2m-1\Leftrightarrow x=2m+2\)
\(\Rightarrow y=x+1=2m+3\)
2 đường thẳng cắt nhau tại 1 điểm nằm trong góc phần tư thứ II khi:
\(\left\{{}\begin{matrix}2m+2< 0\\2m+3>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< -1\\m>-\dfrac{3}{2}\end{matrix}\right.\) \(\Rightarrow-\dfrac{3}{2}< m< -1\)
2 trục tung - hoành của hệ trục tọa độ cắt nhau chia mặt phẳng tọa độ làm 4 phần đánh dấu theo thứ tự ngược chiều kim đồng hồ, góc phần tư thứ I là phần tương ứng từ 12 giờ đến 3 giờ (ứng với x;y đều dương), góc phần tư thứ II từ 9 giờ đến 12h ( x âm y dương), góc III từ 6h đến 9h (x;y đều âm), góc IV từ 3h đến 6h (x dương y âm)
b.
\(\Delta'=m^2-6m+9=\left(m-3\right)^2\ge0;\forall m\) nên pt luôn có 2 nghiệm
Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=-6\\x_1x_2=6m-m^2\end{matrix}\right.\)
Do \(x_1\) là nghiệm nên \(x_1^2+6x_1+6m-m^2=0\Leftrightarrow2x_1^2+12x_1=2m^2-12m\)
Từ đó:
\(x_1^3-x_2^3+2x_1^2+12x_1+72=0\)
\(\Leftrightarrow\left(x_1-x_2\right)\left(\left(x_1+x_2\right)^2-x_1x_2\right)+2m^2-12m+72=0\)
\(\Leftrightarrow\left(x_1-x_2\right)\left(36+m^2-6m\right)+2\left(m^2-6m+36\right)=0\)
\(\Leftrightarrow\left(x_1-x_2+2\right)\left(m^2-6m+36\right)=0\)
Do \(m^2-6m+36=\left(m-3\right)^2+27>0;\forall m\)
\(\Rightarrow x_1-x_2+2=0\)
Kết hợp \(x_1+x_2=-6\) \(\Rightarrow\left\{{}\begin{matrix}x_1-x_2=-2\\x_1+x_2=-6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=-4\\x_2=-2\end{matrix}\right.\)
Thế vào \(x_1x_2=6m-m^2\)
\(\Rightarrow6m-m^2=8\Rightarrow m^2-6m+8=0\Rightarrow\left[{}\begin{matrix}m=2\\m=4\end{matrix}\right.\)