Xét tính đơn điệu của hàm số :
\(y=e^{3x^2-2x-1}\)
Những câu hỏi liên quan
xét tính đơn điệu của các hàm số sau :
a) y=1/2x+5
b)y=3x-1
c)y=|2x-1|
d)y=\(\sqrt{x^2}+6x+9\)
e)y=|1-x| +|2x+4|
f) y=\(\sqrt{x^2-4+4}\)-2|x-1|
Bài 1: Xét tính đơn điệu của hàm số yf(x) khi biết đạo hàm của hàm số là:a) f(x)(x+1)(1-x^2)(2x-1)^3b) f(x)(x+2)(x-3)^2(x-4)^3Bài 2: Cho hàm số yf(x) có đạo hàm f(x)x(x+1)(x-2). Xét tính biến thiên của hàm số:a) yf(2-3x)b) yf(x^2+1)c) yf(3x+1)
Đọc tiếp
Bài 1: Xét tính đơn điệu của hàm số \(y=f(x)\) khi biết đạo hàm của hàm số là:
a) \(f'(x)=(x+1)(1-x^2)(2x-1)^3\)
b) \(f'(x)=(x+2)(x-3)^2(x-4)^3\)
Bài 2: Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=x(x+1)(x-2)\). Xét tính biến thiên của hàm số:
a) \(y=f(2-3x)\)
b) \(y=f(x^2+1)\)
c) \(y=f(3x+1)\)
xét tính đơn điệu của hàm số y=\(\dfrac{-x^2+2x-1}{x+2}\)
TXĐ: D = R \ {-2}
Ta có: \(y'=\dfrac{\left(-2x+2\right)\left(x+2\right)-\left(-x^2+2x-1\right)}{\left(x+2\right)^2}=\dfrac{-x^2-4x+5}{\left(x+2\right)^2}\)
\(y'=0\Rightarrow-x^2-4x+5=0\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=1\end{matrix}\right.\)
⇒ Hàm số y đồng biến trên (-5, -2) và (-2, 1)
Hàm số y nghịch biến trên (-∞, -5) và (1, +∞)
Đúng 0
Bình luận (0)
16 tháng 9 2023 lúc 10:46
Xét tính đơn điệu của hàm số (có vẽ bảng biến thiên)
\(y = \sqrt{2x - x^3}\)
ĐKXĐ: \(2x-x^3\ge0\)
=>\(x^3-2x\le0\)
=>\(x\left(x^2-2\right)\le0\)
TH1: \(\begin{cases}x\ge0\\ x^2-2\le0\end{cases}\Rightarrow\begin{cases}x\ge0\\ x^2\le2\end{cases}\)
=>\(\begin{cases}x\ge0\\ -\sqrt2\le x\le\sqrt2\end{cases}\Rightarrow0\le x\le\sqrt2\)
TH2: \(\begin{cases}x\le0\\ x^2-2\ge0\end{cases}\Rightarrow\begin{cases}x\le0\\ x^2\ge2\end{cases}\)
=>\(\begin{cases}x\le0\\ \left[\begin{array}{l}x\ge\sqrt2\\ x\le-\sqrt2\end{array}\right.\Rightarrow x\le-\sqrt2\end{cases}\)
\(y=\sqrt{2x-x^3}\)
=>\(y^{\prime}=\frac{\left(2x-x^3\right)^{\prime}}{2\cdot\sqrt{2x-x^3}}=\frac{2-3x^2}{2\cdot\sqrt{2x-x^3}}\)
Đặt y'>0
=>\(2-3x^2>0\)
=>\(-3x^2>-2\)
=>\(3x^2<2\)
=>\(x^2<\frac23\)
=>\(-\frac{\sqrt6}{3}
Kết hợp ĐKXĐ, ta được: \(0
=>Hàm số đồng biến trên khoảng \(\left(0;\frac{\sqrt6}{3}\right)\)
Đặt y'<0
=>\(2-3x^2<0\)
=>\(-3x^2<-2\)
=>\(3x^2>2\)
=>\(x^2>\frac23=\frac69\)
=>\(\left[\begin{array}{l}x>\frac{\sqrt6}{3}\\ x<-\frac{\sqrt6}{3}\end{array}\right.\)
Kết hợp ĐKXĐ, ta được: \(\left[\begin{array}{l}\frac{\sqrt6}{3}
=>Hàm số nghịch biến trên các khoảng \(\left(\frac{\sqrt6}{3};\sqrt2\right);\left(-\infty;-\sqrt2\right)\)
Đúng 0
Bình luận (0)
Xét tính đơn điệu của hàm số :
\(y=x+\ln\left(1-2x\right)\)
Tập xác định \(x< \frac{1}{2}\)
Ta có : \(y'=1-\frac{2}{1-2x}=\frac{-1-2x}{1-2x}\Rightarrow y'=0\Leftrightarrow x=-\frac{1}{2}\)
Hàm số đồng biến trên \(\left(-\infty;-\frac{1}{2}\right)\)
Hàm số nghịch biến trên \(\left(-\frac{1}{2};\frac{1}{2}\right)\)
Đúng 0
Bình luận (0)
Xét tính đơn điệu và vẽ đồ thị hàm số sau:
A)y=2x+1
B)y=-x+1
C)y=\(\dfrac{1-x}{2}\)
D)y=\(\dfrac{-x}{4}\)+2
a: Hàm số đồng biến trên R
b: Hàm số nghịch biến trên R
Đúng 0
Bình luận (0)
Xét tính đơn điệu của hàm số: f(x) = 2x - sin2x
\(f'\left(x\right)=2-2cos2x\)
\(f'\left(x\right)=0\Leftrightarrow x=0\)
Hàm số đồng biến trên khoảng \(\left(0;+\infty\right)\)
Hàm số nghịch biến trên khoảng \(\left(-\infty;0\right)\)
Đúng 1
Bình luận (0)
Cho hàm số: y = 4 - x 2 x + 3 m
Xét tính đơn điệu của hàm số.
Xét hàm số:
y
=
4
-
x
2
x
+
3
m
TXĐ: R \ {−3m/2}
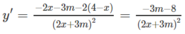
+) Nếu m < −8/3, y′ > 0 suy ra hàm số đồng biến trên các khoảng 
+) Nếu m > −8/3, y′ < 0 suy ra hàm số nghịch biến trên các khoảng
+) Nếu m = −8/3 thì y = −1/2 khi x ≠ 4
Đúng 0
Bình luận (0)
Xét tính đơn điệu của hàm số:
y= x4- 2x2
TXĐ: `D=RR`
`y'=x^3-4x`
`y'=0 <=>` \(\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
\(\begin{array}{|l|cr|} \hline x & -\infty & & -2 &&&& & 0 & &&&&2&&& & +\infty\\ \hline y' & &-& 0& & &+& &0& &&-&&0& &&+&\\ \hline\end{array}\)
Vậy hàm số đồng biến trên các khoảng: `(-2;0)` và `(2; +\infty)`
Hàm số nghịch biến trên các khoảng: `(-\infty; -2)` và `(0;2)`.
Đúng 3
Bình luận (0)