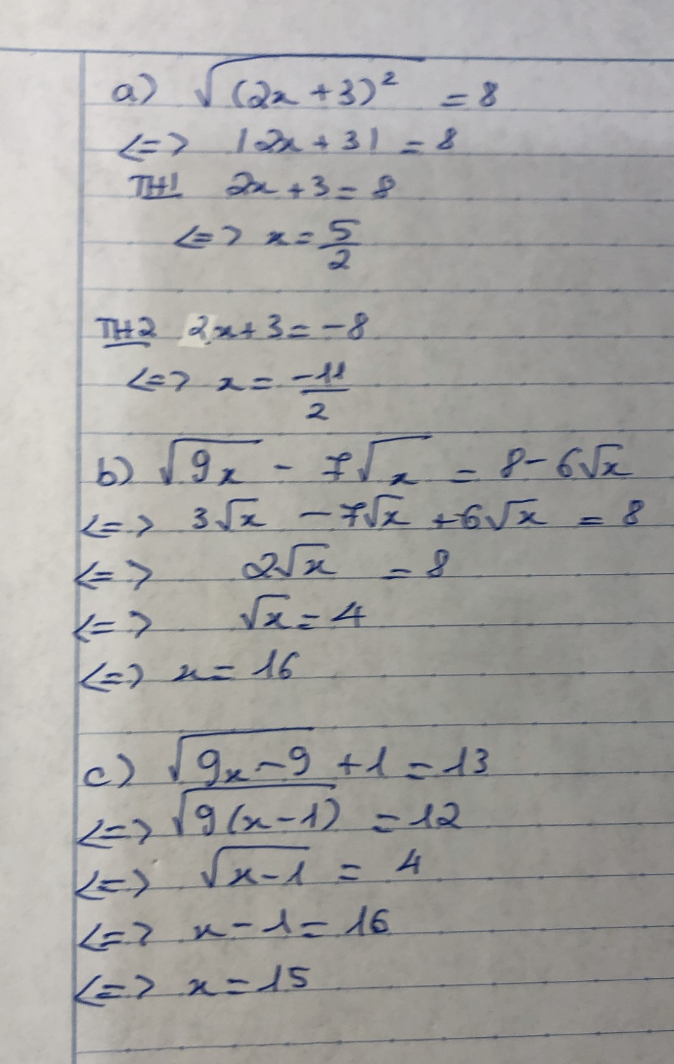b, ĐKXĐ : \(\left\{{}\begin{matrix}x>0\\x\ne4\end{matrix}\right.\)

Ta có : \(B=\dfrac{\left(\sqrt{x}-2\right)\left(x+2\sqrt{x}+4\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}-\dfrac{\left(\sqrt{x}+2\right)\left(x-2\sqrt{x}+4\right)}{\sqrt{x}\left(\sqrt{x}+2\right)}+\dfrac{x+2}{\sqrt{x}}\)

\(=\dfrac{x+2\sqrt{x}+4}{\sqrt{x}}-\dfrac{x-2\sqrt{x}+4}{\sqrt{x}}+\dfrac{x+2}{\sqrt{x}}\)

\(=\dfrac{x+2\sqrt{x}+4-x+2\sqrt{x}-4+x+2}{\sqrt{x}}\)

\(=\dfrac{x+4\sqrt{x}+2}{\sqrt{x}}\)

b) Ta có: \(B=\dfrac{x\sqrt{x}-8}{x-2\sqrt{x}}-\dfrac{x\sqrt{x}+8}{x+2\sqrt{x}}+\dfrac{x+2}{\sqrt{x}}\)

\(=\dfrac{x+2\sqrt{x}+4}{\sqrt{x}}-\dfrac{x-2\sqrt{x}+4}{\sqrt{x}}+\dfrac{x+2}{\sqrt{x}}\)

\(=\dfrac{4\sqrt{x}+x+2}{\sqrt{x}}\)

c) Ta có: \(C=\dfrac{1}{\sqrt{x}+2}-\dfrac{5}{x-\sqrt{x}-6}-\dfrac{\sqrt{x}-2}{3-\sqrt{x}}\)

\(=\dfrac{\sqrt{x}-3-5+\left(x-4\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{x+\sqrt{x}-12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{\sqrt{x}+4}{\sqrt{x}+2}\)

a) Đặt $\sqrt{x+1}=a; \sqrt{9-x}=b$ thì bài toán trở thành:

Tìm max, min của $f(a,b)=a+b$ với $a,b\geq 0$ và $a^2+b^2=10$Ta có:

$f^2(a,b)=(a+b)^2=a^2+b^2+2ab=10+2ab\geq 10$ do $ab\geq 0$

$\Rightarrow f(a,b)\geq \sqrt{10}$ hay $f_{\min}=\sqrt{10}$

Mặt khác: $f^2(a,b)=(a+b)^2\leq 2(a^2+b^2)=20$ (theo BĐT AM-GM)

$\Rightarrow f(a,b)\leq \sqrt{20}=2\sqrt{5}$ hay $f_{\max}=2\sqrt{5}$

b) 

Đặt $\sqrt{x}=a; \sqrt{2-x}=b$ thì bài toán trở thành:

Tìm max, min của $f(a,b)=a+b+ab$ với $a,b\geq 0$ và $a^2+b^2=2$. Ta có:

$f(a,b)=\sqrt{(a+b)^2}+ab=\sqrt{a^2+b^2+2ab}+ab=\sqrt{2+2ab}+ab\geq \sqrt{2}$ do $ab\geq 0$

Vậy $f_{\min}=\sqrt{2}$

Lại có, theo BĐT AM-GM:

$f(a,b)=\sqrt{2+2ab}+ab\leq \sqrt{2+a^2+b^2}+\frac{a^2+b^2}{2}=\sqrt{2+2}+\frac{2}{2}=3$

Vậy $f_{\max}=3$

c) Đặt $\sqrt{8-x^2}=a$ thì bài toán trở thành tìm max, min của:

$f(x,a)=x+a+ax$ với $x,a\geq 0$ và $x^2+a^2=8$. Bài này chuyển về y hệt  như phần b. 

$f_{\min}=2\sqrt{2}$

$f_{\max}=8$

d) Tương tự:

$f_{\min}=2$ khi $x=\pm 2$

$f_{\max}=2+2\sqrt{2}$ khi $x=0$

\(a,=\dfrac{\sqrt{x}-8+5}{\sqrt{x}-8}=1+\dfrac{5}{\sqrt{x}-8}\in Z\\ \Leftrightarrow\sqrt{x}-8\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Leftrightarrow\sqrt{x}\in\left\{3;7;9;13\right\}\\ \Leftrightarrow x\in\left\{9;49;81;169\right\}\left(tm\right)\\ b,=\dfrac{\sqrt{x}-2+7}{\sqrt{x}-2}=1+\dfrac{7}{\sqrt{x}-2}\in Z\\ \Leftrightarrow\sqrt{x}-2\inƯ\left(7\right)=\left\{-1;1;7\right\}\left(\sqrt{x}-2>-2\right)\\ \Leftrightarrow\sqrt{x}\in\left\{1;3;9\right\}\\ \Leftrightarrow x\in\left\{1;9;81\right\}\\ c,=\dfrac{2\left(\sqrt{x}+3\right)+2}{\sqrt{x}+3}=2+\dfrac{2}{\sqrt{x}+3}\in Z\\ \Leftrightarrow\sqrt{x}+3\inƯ\left(2\right)=\varnothing\left(\sqrt{x}+3>3\right)\\ \Leftrightarrow x\in\varnothing\)

1) \(ĐK:x\in R\)

2) \(ĐK:x< 0\)

3) \(ĐK:x\in\varnothing\)

4) \(=\sqrt{\left(x+1\right)^2+2}\) 

\(ĐK:x\in R\)

5) \(=\sqrt{-\left(a-4\right)^2}\)

\(ĐK:x\in\varnothing\)

a: ĐKXĐ: x>0; x<>4

\(P=\left(2-\sqrt{x}+2\right)\cdot\dfrac{1}{\sqrt{x}-2}=\dfrac{4-\sqrt{x}}{\sqrt{x}-2}\)

b: P=2/3

=>(4-căn x)/(căn x-2)=2/3

=>2căn x-4=12-3căn x

=>5căn x=16

=>x=256/25

c: Khi x=8-2căn 7 thì \(P=\dfrac{4-\sqrt{7}+1}{\sqrt{7}-1-2}=\dfrac{5-\sqrt{7}}{\sqrt{7}-3}=-4-\sqrt{7}\)

a) ⇔ |2x+3| = 8
⇒ \(\left[{}\begin{matrix}2x+3=8\\2x+3=-8\end{matrix}\right.\) ⇔ \(\left[{}\begin{matrix}2x=5\\2x=-11\end{matrix}\right.\) ⇔ \(\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{11}{2}\end{matrix}\right.\)

Vậy...

b) ĐKXĐ: \(x\ge0\)

\(\Leftrightarrow3\sqrt{x}-7\sqrt{x}+6\sqrt{x}=8\)

\(\Leftrightarrow2\sqrt{x}=8\)

\(\Leftrightarrow\sqrt{x}=4\)

\(\Leftrightarrow x=16\) (Vì \(x\ge0\) )

Vậy x = 16

c) ĐKXĐ: \(x\ge1\)

\(\Leftrightarrow\sqrt{9\left(x-1\right)}=12\)

\(\Leftrightarrow3\sqrt{x-1}=12\)

\(\Leftrightarrow\sqrt{x-1}=4\)

\(\Leftrightarrow x-1=16\)

\(\Leftrightarrow x=17\)(TM)

Vậy x = 17

em tham khảo