Một vật dao động điều hòa với x = \(6cos\left(5\pi.t-\dfrac{\pi}{4}\right)\) cm . Xác định thời điểm lần thứ hai vật có vận tốc v = \(-15\pi\) (cm/s) .

Những câu hỏi liên quan
1) 1 dao động điều hòa với phương trình v3pi cosleft(pi tright)cm/s. xác định tốc độ cực đại, tần số góc, chu kì, tần số, pha ban đầu và tính vận tốc tại thời điểm t 3s2) một vật dao động điều hòa có phương trình gia tốc a4pi^2cosleft(pi t-dfrac{pi}{2}right)xác định gia tốc cực đại, tần số góc, chu kì và pha ban đầu của gia tốc
Đọc tiếp
1) 1 dao động điều hòa với phương trình \(v=3\pi cos\left(\pi t\right)\)cm/s. xác định tốc độ cực đại, tần số góc, chu kì, tần số, pha ban đầu và tính vận tốc tại thời điểm t = 3s
2) một vật dao động điều hòa có phương trình gia tốc \(a=4\pi^2cos\left(\pi t-\dfrac{\pi}{2}\right)\)xác định gia tốc cực đại, tần số góc, chu kì và pha ban đầu của gia tốc
1 vật dao động điều hòa với phương trình vận tốc như sau \(v=5\pi cos\left(\pi t+\dfrac{\pi}{3}\right)\)cm/s
a) xác định tốc độ cực đại, tần số góc, chu kì và pha ban đầu của vận tốc
b) thời điểm t = 0,25s vận tốc có giá trị
a)\(v_{max}=\omega A=5\pi^2\approx50\left(cm/s\right)\)
Tần số góc: \(\omega=\pi\left(rad\right)\)
Chu kì: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{\pi}=2s\)
Pha ban đầu của vận tốc: \(\varphi=\dfrac{\pi}{3}\)
b)Tại thời điểm \(t=0,25s\):
\(\Rightarrow v=5\pi cos\left(\pi\cdot0,25+\dfrac{\pi}{3}\right)\approx-4,065m/s\)
Đúng 2
Bình luận (0)
v5pi cosleft(4pi t-dfrac{pi}{2}right)10����(��+�3)cm/s. Hãy xác định tốc độ cực đại, tần số góc, chu kì, tần số và pha ban đầu của vận tốc
Đọc tiếp
cm/s. Hãy xác định tốc độ cực đại, tần số góc, chu kì, tần số và pha ban đầu của vận tốc
Pha ban đầu là \(4pi\cdot t-\dfrac{pi}{2}\)
Tần số là \(f=\dfrac{4pi}{2pi}=2\)
Chu kì là \(T=\dfrac{1}{f}=\dfrac{1}{2}\)
Tần số góc là \(w=2pi:\dfrac{1}{2}=4pi\)
Đúng 0
Bình luận (0)
Một vật dao động điều hòa theo phương trình: \(x=4\cos\left(6\pi t+\dfrac{\pi}{6}\right)\left(cm\right)\). Vận tốc của vật đạt giá trị \(12\pi\) (cm/s) khi vật đi qua li độ
\(v=x'=6pi\cdot4\cdot cos\left(6pi\cdot t+\dfrac{pi}{6}+\dfrac{pi}{2}\right)\)
\(=24pi\cdot cos\left(6pi\cdot t+\dfrac{2}{3}pi\right)\)
v'=12pi
=>cos(6pi*t+2/3pi)=1/2
=>6pi*t+2/3pi=pi/3+k2pi hoặc 6pi*t+2/3pi=-pi/3+k2pi
=>6pi*t=-1/3pi+k2pi hoặc 6pi*t=-pi+k2pi
=>t=-1/18+k/3 hoặc t=-1/6+k/3
Đúng 2
Bình luận (0)
1 vật đang dao động điều hòa với phương trình vận tốc như sau: \(v=10\pi cos\left(\pi t+\dfrac{\pi}{3}\right)\)cm/s. Hãy xác định tốc độ cực đại, tần số góc, chu kì, tần số và pha ban đầu của vận tốc
\(v_{max}=10\pi\left(\dfrac{cm}{s}\right)\\ \omega=\pi\left(\dfrac{rad}{s}\right)\\T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{\pi}=2\left(s\right)\\ f=\dfrac{1}{T}=\dfrac{1}{2}\left(Hz\right)\\ \varphi=\dfrac{\pi}{3}\)
Đúng 1
Bình luận (0)
Một vật nhỏ thực hiện dao động điều hòa với phương trình \(x=5\cos\left(4\pi t-\dfrac{\pi}{3}\right)\left(cm\right)\). Tại thời điểm t1, vật có li độ \(2,5\sqrt{2}\left(cm\right)\) và đang có xu hướng giảm. Li độ của vật sau thời điểm đó \(\dfrac{7}{48}\left(s\right)\) là
Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{4\pi}=0,5s\)
Ta có: \(x=2,5\sqrt{2}=\dfrac{A\sqrt{2}}{2}\) và đang có xu hướng giảm.
Lúc này vật ở thời điểm: \(t_1=\dfrac{T}{8}\)
Tại thời điểm: \(t=\dfrac{7}{48}s=\dfrac{7T}{14}=\dfrac{T}{8}+\dfrac{T}{6}\)
Dựa vào vòng tròn lượng giác \(\Rightarrow x=2,5cm\)
Đúng 2
Bình luận (1)
Bài1: 1 vật dao động điều hòa với phương trình: x-5cosleft(10pi t+dfrac{pi}{2}right)cm. Hãy xác định biên độ, tần số góc, chu kì và pha ban đầu của dao động tại thời điểm t 1sBài 2: 1 vật dao động điều hòa với phương trình: x-3cosleft(2pi t+piright)cm. Hãy xác định biên độ, tần số góc, chu kì và pha ban đầu của dao động tại thời điểm t 0,5s
Đọc tiếp
Bài1: 1 vật dao động điều hòa với phương trình: \(x=-5cos\left(10\pi t+\dfrac{\pi}{2}\right)cm\). Hãy xác định biên độ, tần số góc, chu kì và pha ban đầu của dao động tại thời điểm t = 1s
Bài 2: 1 vật dao động điều hòa với phương trình: \(x=-3cos\left(2\pi t+\pi\right)cm\). Hãy xác định biên độ, tần số góc, chu kì và pha ban đầu của dao động tại thời điểm t = 0,5s
2:
\(x=-3\cdot cos\left(2pi\cdot t+pi\right)\)
\(=3\cdot cos\left(pi+2pi\cdot t+pi\right)\)
\(=3\cdot cos\left(2pi\cdot t+2pi\right)\)
Biên độ là A=3
Tần số góc là 2pi
Chu kì là T=2pi/2pi=1
Pha ban đầu là 2pi
Pha của dao động tại thời điểm t=0,5 giây là;
\(2pi\cdot0.5+2pi=3pi\)
Đúng 0
Bình luận (0)
bài 1:
Biên độ góc: A = 5 cm
Tần số góc = 10 pi
Chu kì T = 2pi / tần số góc = 0,2 s
pha dao động là 10 pi x 1 - pi /2 = 19/ 2 pi
Đúng 0
Bình luận (0)
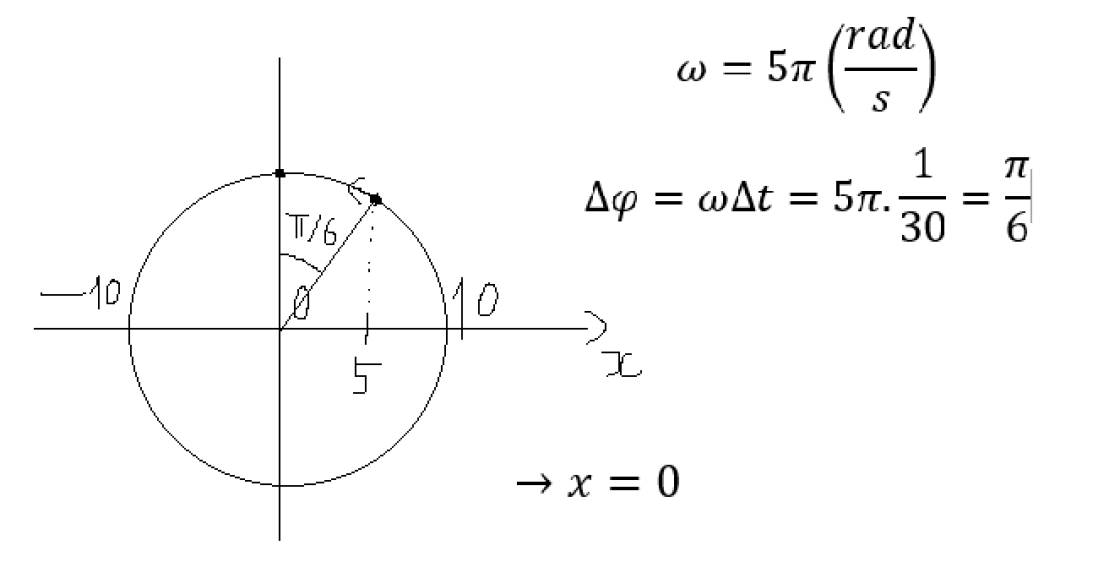
Dùng phương pháp đường tròn lượng giác hãy giải :
Vật dao động điều hoà với phương trình \(x=10cos\left(5\pi t+\dfrac{\pi}{3}\right)cm\) . Tại thời điểm t vật có li độ 5 cm , xác định li dộ của vật sau đó \(\dfrac{1}{30}s\)
(kèm hình vẽ)
cho pt dao động x=6cos(5pi.t- pi/4) cm . tính từ lúc khảo bắt đầu khảo sát dao động, lần thứ hai vật có vận tốc v2= -15pi cm/s vao thời điểm nao?
thầy chỉ em cach xác đinh v trên đương trong với nó cho v chả biết x là bao nhiêu dấu trừ hay dâu + mà vẽ trên đường tròn ?
Dùng công thức độc lập \(A^2=x^2+\frac{v^2}{\omega^2}\), tìm đc x (cả dấu + và - )
Vẽ vòng tròn, vật đạt vận tốc âm khi véc tơ quay ở nửa trên vòng tròn (Có 2 vị trí )
Cho véc tơ quay đến vị trí thứ 2 thỏa mãn là đc.
Đúng 0
Bình luận (3)
Xem thêm câu trả lời