Rút gọn bt sau \(\dfrac{1}{2+\sqrt{3}}+\sqrt{3}\)

Những câu hỏi liên quan
rút gọn bt sau \(\dfrac{\sqrt{8-2\sqrt{12}}}{\sqrt{3}-1}\)
Ta có: \(\dfrac{\sqrt{8-2\sqrt{12}}}{\sqrt{3}-1}\)
\(=\dfrac{\sqrt{\left(\sqrt{6}-\sqrt{2}\right)^2}}{\sqrt{3}-1}\)
\(=\sqrt{2}\)
Đúng 2
Bình luận (0)
rút gọn bt sau \(\dfrac{2\sqrt{3}}{\sqrt{3+\sqrt{2}}}+\sqrt{24}\)
Ta có: \(\dfrac{2\sqrt{3}}{\sqrt{3}+\sqrt{2}}+\sqrt{24}\)
\(=2\sqrt{3}\left(\sqrt{3}-\sqrt{2}\right)+2\sqrt{6}\)
\(=6-2\sqrt{6}+2\sqrt{6}\)
=6
Đúng 3
Bình luận (0)
Bài 1: Rút gọn bt
\(\dfrac{6}{\sqrt{2}-\sqrt{3}+3}\)
\(\dfrac{6}{\sqrt{2}-\sqrt{3}+3}\)
\(=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{\left(\sqrt{2}-\sqrt{3}\right)^2-9}\)
\(=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{-4-2\sqrt{6}}\)
\(=\dfrac{-3\left(\sqrt{2}-\sqrt{3}-3\right)}{2+\sqrt{6}}=\dfrac{-3\left(\sqrt{6}-2\right)\left(\sqrt{2}-\sqrt{3}-3\right)}{2}\)
Đúng 1
Bình luận (0)
Rút gọn bt A=\(\left(\dfrac{1+\sqrt{x}}{x+1}-\dfrac{4-3\sqrt{x}}{x-4\sqrt{x}+4}\right):\left(\dfrac{x-\sqrt{x}}{x\sqrt{x}-2x+\sqrt{x}-2}\right)\)
Sau đó tìm x để A>1
Ta có: \(A=\left(\dfrac{\sqrt{x}+1}{x+1}-\dfrac{4-3\sqrt{x}}{x-4\sqrt{x}+4}\right):\left(\dfrac{x-\sqrt{x}}{x\sqrt{x}-2x+\sqrt{x}-2}\right)\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(x-4\sqrt{x}+4\right)+\left(3\sqrt{x}-4\right)\left(x+1\right)}{\left(x+1\right)\left(\sqrt{x}-2\right)^2}:\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-2\right)\left(x+1\right)}\)
\(=\dfrac{x\sqrt{x}-4x+4\sqrt{x}+x-4\sqrt{x}+4+3x\sqrt{x}+3\sqrt{x}-4x-4}{\left(x+1\right)\left(\sqrt{x}-2\right)^2}\cdot\dfrac{\left(\sqrt{x}-2\right)\left(x+1\right)}{x-\sqrt{x}}\)
\(=\dfrac{4x\sqrt{x}-7x+3\sqrt{x}}{\sqrt{x}-2}\cdot\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\cdot\left(4\sqrt{x}-3\right)}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{4\sqrt{x}-3}{\sqrt{x}-2}\)
Để A>1 thì A-1>0
\(\Leftrightarrow\dfrac{4\sqrt{x}-3-\sqrt{x}+2}{\sqrt{x}-2}>0\)
\(\Leftrightarrow\dfrac{3\sqrt{x}-1}{\sqrt{x}-2}>0\)
\(\Leftrightarrow\left[{}\begin{matrix}3\sqrt{x}-1\le0\\\sqrt{x}-2>0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}0< x\le\dfrac{1}{9}\\x>4\end{matrix}\right.\)
Đúng 2
Bình luận (0)
a) tính gtrị của biểu thức A = \(\sqrt{3}+\sqrt{12}-\sqrt{27}-\sqrt{36}\)
b) cho bt B = \(\dfrac{2}{\sqrt{x-1}}-\dfrac{1}{\sqrt{x}}+\dfrac{3\sqrt{x-5}}{\sqrt{x\left(\sqrt{x-1}\right)}}\) với x > 0 và x \(\ne\) 1 . rút gọn bt và tìm x để B = 2
\(a,\) ta có :
\(\Leftrightarrow\left\{{}\begin{matrix}A=\sqrt{3}+\sqrt{2^2.3}-\sqrt{3^2.3}-\sqrt{6^2}\\A=\sqrt{3}+2\sqrt{3}-3\sqrt{3}-6\\A=\sqrt{3}.\left(1+2-3\right)-6\\A=-6\end{matrix}\right.\)
\(\Rightarrow A=-6\) . vậy \(A=9\sqrt{5}\)
__________________________________________________________
\(b,\) với \(x>0\) và \(x\ne1\) . ta có :
\(B=\dfrac{2}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}}+\dfrac{3\sqrt{x}-5}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow B=\dfrac{2\sqrt{x}-\left(\sqrt{x}-1\right)+3\sqrt{x}-5}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow B=\dfrac{2\sqrt{x}-\sqrt{x}+1+3\sqrt{x}-5}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow B=\dfrac{4\sqrt{x}-4}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow\) \(B=\dfrac{4\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow B=\dfrac{4}{\sqrt{x}}\)
vậy với \(x>0\) \(;\) \(x\ne1\) thì \(B=\dfrac{4}{\sqrt{x}}\)
để \(B=2\) thì \(\dfrac{4}{\sqrt{x}}=2\Leftrightarrow\sqrt{x}=2\Leftrightarrow x=4\left(tm\right)\)
vậy để \(B=2\) thì \(x=4\)
Đúng 4
Bình luận (1)
cho bt A=\(\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right):\left[\dfrac{2}{x}-\dfrac{2-x}{x\left(\sqrt{x}+1\right)}\right]\)
a)rút gọn bt A
b)tính giá trị của bt A khi\(x=4+2\sqrt{3}\)
c)tìm giá trị của x để bt \(\sqrt{A}\)có giá trị nỏ nhất
ĐKXĐ: \(x>0;x\ne1\)
\(A=\left(\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\left(\dfrac{2\left(\sqrt{x}+1\right)}{x\left(\sqrt{x}+1\right)}-\dfrac{2-x}{x\left(\sqrt{x}+1\right)}\right)\)
\(=\left(\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\left(\dfrac{x+2\sqrt{x}}{x\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{\left(x+2\sqrt{x}\right).x.\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\left(x+2\sqrt{x}\right)}=\dfrac{x}{\sqrt{x}-1}\)
b.
\(x=4+2\sqrt{3}=\left(\sqrt{3}+1\right)^2\Rightarrow\sqrt{x}=\sqrt{3}+1\)
\(\Rightarrow A=\dfrac{4+2\sqrt{3}}{\sqrt{3}+1-1}=\dfrac{4+2\sqrt{3}}{\sqrt{3}}=\dfrac{6+4\sqrt{3}}{3}\)
c.
Để \(\sqrt{A}\) xác định \(\Rightarrow\sqrt{x}-1>0\Rightarrow x>1\)
Ta có:
\(\sqrt{A}=\sqrt{\dfrac{x}{\sqrt{x}-1}}=\sqrt{\dfrac{x}{\sqrt{x}-1}-4+4}=\sqrt{\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}-1}+4}\ge\sqrt{4}=2\)
Dấu "=" xảy ra khi \(\sqrt{x}-2=0\Rightarrow x=4\)
Đúng 0
Bình luận (1)
Cho P =(\(\dfrac{2\sqrt{x}}{\sqrt{x}+3}-\dfrac{\sqrt{x}}{3-\sqrt{x}}-\dfrac{3x+3}{x-9}\)):\(\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\) với x≥0,x≠9
a) rút gọn P
b) tìm x bt P=-1/3
c) So sánh P và -1
\(P=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)+\sqrt{x}\left(\sqrt{x}+3\right)-3x-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}.\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\)
\(=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}.\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\)
\(=\dfrac{-3\sqrt{x}-3}{\left(\sqrt{x}+3\right)^2}\)
\(P=-\dfrac{1}{3}\)
\(\Rightarrow\left(\sqrt{x}+3\right)^2=3\sqrt{x}+3\)
\(\Leftrightarrow x-\sqrt{x}+6=0\)
\(\Leftrightarrow\left(\sqrt{x}+2\right)\left(\sqrt{x}-3\right)=0\)
\(\Leftrightarrow x=9\left(Vì\sqrt{x}+2>0\right)\)
\(P=-\left(\dfrac{3\sqrt{x}+3}{\left(\sqrt{x}+3\right)^2}\right)=-\left(\dfrac{3\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+3\right)^2}\right)< -3< -1\)
Đúng 1
Bình luận (0)
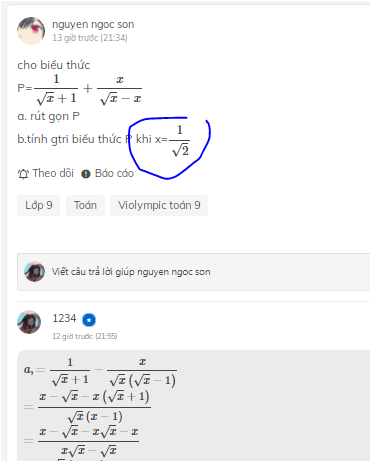
cho biểu thức
P=\(\dfrac{1}{\sqrt{x}+1}+\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
a. rút gọn P
b.tính gtri biểu thức P khi x=1√2
đáp án:
a.P=\(\dfrac{x+1}{1-x}\)
b.P=3+2\(\sqrt{2}\)
mk chỉ bt đáp án chứ ko bt cách giải
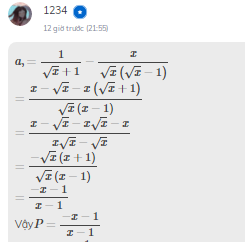
Mk ra đáp án khác với đáp án ủa bn nên bn bào sai chứ j, thật ra cả 2 đáp án đều giống nhau, do biến đổi dấu nên trở thành 2 đáp án khác nhau thôi :V
để mk lm lại phần đáp án của mk ra giống đáp án của bn nek :V
\(a,\)\(P=\dfrac{-x-1}{x-1}\)
\(\Rightarrow\dfrac{-\left(-x-1\right)}{-\left(x-1\right)}=\dfrac{x-1}{-x+1}=\dfrac{x-1}{1-x}\)
Còn câu b thì hôm qua bn ghi là \(x=\dfrac{1}{\sqrt{2}}\) chứ có pk là \(1\sqrt{2}\) đou >:V
\(b,\)Thay \(x=1\sqrt{2}\) vào \(P\) ta có :
\(P=\dfrac{x-1}{1-x}\)
\(P=\dfrac{1\sqrt{2}-1}{1-1\sqrt{2}}=3+2\sqrt{2}\)
Đúng 0
Bình luận (1)
rút gọn bt sau: a=\(\left(\dfrac{x-1}{\sqrt{x}-1}+\dfrac{x\sqrt{x}-a}{1-x}\right):\left(\dfrac{\left(\sqrt{x}-1\right)^2+\sqrt{x}}{\sqrt{x}+1}\right)\)
Đoạn $x\sqrt{x}-a$ là sao vậy bạn? Có nhầm lẫn gì không?
Đúng 1
Bình luận (1)
\(=\left(\sqrt{x}+1-\dfrac{x+\sqrt{x}+1}{\sqrt{x}+1}\right):\dfrac{x-\sqrt{x}+1}{\sqrt{x}+1}\)
\(=\dfrac{x+2\sqrt{x}+1-x-\sqrt{x}-1}{\sqrt{x}+1}\cdot\dfrac{\sqrt{x}+1}{x-\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}}{x-\sqrt{x}+1}\)
Đúng 0
Bình luận (0)



















