Cho hình thoi ABCD có AB = a, \(\widehat{BAD}\) = 2α (0° < α < 90°). Chứng minh:
a) BD = 2a.sinα;
b) AC = 2a.cosα.
Cho hình hộp đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a. \(\widehat{BAD}=120^0;\widehat{BA'D}=90^0\). Tính thể tích hình hộp theo a ?
Cho hình thoi \(ABCD\). Hãy chứng tỏ:
a) Nếu \(\widehat {BAD}\) là góc vuông thì ba góc còn lại của hình thoi cũng là góc vuông.
b) Nếu \(AC = BD\) thì \(\widehat {BAD}\) là góc vuông
a)
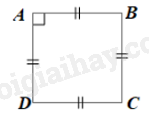
\(ABCD\) là hình thoi nên cũng là hình bình hành.
Suy ra:
\(AB = BC = CD = DA\);
\(\widehat A = \widehat C;\;\widehat B = \widehat D\)
\(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
Suy ra: \(\widehat A + \widehat B = \widehat C + \widehat D = 180^\circ \)
Mà \(\widehat {BAD}\) là góc vuông
Suy ra \(\widehat {BCD} = 90^\circ \); \(\widehat B = 90^\circ ;\;\widehat D = 90^\circ \)
b) Nếu \(AC = BD\) thì \(ABCD\) là hình chữ nhật
Khi đó \(\widehat {BAD}\) là góc vuông
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi, cạnh a; \(\widehat{BAD}=60^0\). Biết \(AB'\perp BD'\). Tính thể tích khối lăng trụ \(\left(V=S_đ.h\right)\)
Đặt \(x=AA'\)
Ta có: \(\overrightarrow{AB'}=\overrightarrow{AA'}+\overrightarrow{AB}\) ; \(\overrightarrow{BD'}=\overrightarrow{BB'}+\overrightarrow{BD}=\overrightarrow{BB'}+\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{AA'}-\overrightarrow{AB}+\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{AB'}.\overrightarrow{BD'}=\left(\overrightarrow{AA'}+\overrightarrow{AB}\right)\left(\overrightarrow{AA'}-\overrightarrow{AB}+\overrightarrow{BC}\right)\)
\(=AA'^2+\overrightarrow{AA'}\left(-\overrightarrow{AB}+\overrightarrow{BC}\right)+\overrightarrow{AB}.\overrightarrow{AA'}-AB^2+\overrightarrow{AB}.\overrightarrow{BC}\)
\(=x^2-a^2+AB.BC.cos120^0\)
\(=x^2-a^2-\dfrac{a^2}{2}=x^2-\dfrac{3a^2}{2}=0\)
\(\Rightarrow x=\dfrac{a\sqrt{6}}{2}\)
\(V=\dfrac{a\sqrt{6}}{2}.2.\dfrac{a^2\sqrt{3}}{4}=\dfrac{3a^3\sqrt{2}}{4}\)
Cho hình thoi ABCD, \(\widehat{A}=90^0\), O là giao điểm hai đường chéo, vẽ OF vuông góc với AB (F\(\in\)AB).
a) Chứng minh đường tròn tâm O, bán kính OF tiếp xúc với bốn cạnh của hình thoi ABCD.
b) Đường tròn ngoại tiếp tam giác ABD cắt AC tại điểm thứ hai K. Chứng minh K là trực tâm của tam giác BCD.
c) Cho biết \(\widehat{BAD}=60^0\), cạnh AB=a
i. Tính diện tích hình thoi ABCD theo a
ii. Chứng minh rằng \(\frac{AO}{OK}=\frac{ÃC}{CK}\)
Cho hình thoi ABCD có \(\widehat{BAD}=30^o,AB=6.2cm\). Tính diện tích hình thoi.
Cho hình thoi ABCD có \(\widehat{ABC}< 90^0\). Gọi O là giao điểm của 2 đường chéo AC và BD. Kẻ OH vuông góc với BC. Gọi M và N là 2 điểm lần lượt thuộc DC và DA, sao cho \(\widehat{MON}=\widehat{DAC}\). Chứng minh rằng 3 đường thẳng BM ; HN và AC đồng quy tại I
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán hỗ trợ giúp đỡ em tham khảo với ạ!
Em cám ơn nhiều lắm ạ!
Cho Hình 44 có AC = BD, \(\widehat {ABC} = \widehat {BAD} = 90^\circ \). Chứng minh AD = BC.
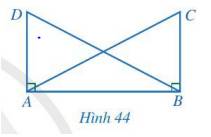
Xét hai tam giác vuông DAB và CBA: AC = BD; AB chung.
Nên \(\Delta DAB = \Delta CBA\) (cạnh huyền - cạnh góc vuông)
Nên AD = BC ( 2 cạnh tương ứng)
Hình thang ABCD có \(\widehat{D}=\widehat{A}=90^0\); AB = 30cm; CD = 18cm; BC = 20cm
a. Tính \(\widehat{ABC};\widehat{BCD}\)
b. Tính \(\widehat{DAC};\widehat{ADB}\)
c. Tính BD, AC
Cho hình thang ABCD có \(\widehat{B}=\widehat{C}=90^O\). Hai đường chéo vuông góc với nhau tại H. Biết AB = \(3\sqrt{5}\) cm, HA = 3cm. Chứng minh:
a) HA:HB:HC:HD = 1:2:4:8
b) \(\dfrac{1}{AB^2}-\dfrac{1}{CD^2}=\dfrac{1}{HB^2}-\dfrac{1}{HC^2}\)
Cho hình chóp S.ABCD, đáy ABCD là hình thoi cạnh a, \(\widehat{BAD}=60^0,SA=SB=SD=a\)
a) Chứng minh (SAC) vuông góc với (ABCD)
b) Chứng minh tam giác SAC vuông
c) Tính khoảng cách từ S đến (ABCD)