Giup mình câu a với ạ
Bài 6: Ôn tập chương Vecơ trong không gian. Quan hệ vuông góc trong không gian.
chop chóp S.ABCD ,ABCD là hình vuông cạnh a, SA vuông góc với ABCD biết SA =a\(\sqrt{3}\) .chứng minh: a:các mặt bên của chóp là những tam giác vuông
b:tính góc giữa SC và (SAB)
c:gọi M là trung điểm của SC .CM:AM vuông góc với BD
Cho tứ diện ABCD có tam giác BCD là tam giác đều , gọi BH là đường cao của tam giác BCD . O là trung điểm của BH và AO vuông góc (BCD), AO=BH=2a, trên OH lấy điểm I sao cho BI=x, (a<x<2a), mặt phẳng (P) đi qua I và vuông góc OH. Dựng thiết và tính diện tích thiết diện của tứ diện tạo bởi (P)
Ai giãi cho mình đè này zoi minh thi song cần gấp lám

\(\left[\dfrac{3\sqrt{a}}{\sqrt{a}+4}+\dfrac{\sqrt{a}}{\sqrt{a}-4}+\dfrac{4\left(a+2\right)}{16-a}\right]:\left(1-\dfrac{2\sqrt{a}+5}{\sqrt{a}+4}\right)\)
a\(\ge\)0 ; a\(\ne\)16
a, rút gọn B
b, tìm a để B= -3
c, tìm các giá trị nguyên của a để B có giá trị nguyên
a)ĐKXĐ:\(a\ge0;a\ne16\)
\(B=\left[\dfrac{3\sqrt{a}}{\sqrt{a}+4}+\dfrac{\sqrt{a}}{\sqrt{a}-4}+\dfrac{4\left(a+2\right)}{16-a}\right]:\left(1-\dfrac{2\sqrt{a}+5}{\sqrt{a}+4}\right)\)
=\(\dfrac{3\sqrt{a}\left(\sqrt{a}-4\right)+\sqrt{a}\left(\sqrt{a}+4\right)-4\left(a+2\right)}{a-16}:\dfrac{\sqrt{a}+4-2\sqrt{a}-5}{\sqrt{a}+4}=\dfrac{3a-12\sqrt{a}+a+4\sqrt{a}-4a-8}{\left(\sqrt{a}-4\right)\left(\sqrt{a}+4\right)}\cdot\dfrac{\sqrt{a}+4}{-\sqrt{a}-1}=\dfrac{-8\sqrt{a}-8}{\left(\sqrt{a}-4\right)\left(-\sqrt{a}-1\right)}=\dfrac{8\left(-\sqrt{a}-1\right)}{\left(\sqrt{a}-4\right)\left(-\sqrt{a}-1\right)}=\dfrac{8}{\sqrt{a}-4}\)
Vậy...
b)Với \(a\ge0;a\ne16\) thì B=\(\dfrac{8}{\sqrt{a}-4}\)
B=-3 thì \(\dfrac{8}{\sqrt{a}-4}=-3\)
=>\(9=-3\sqrt{a}+24\)
<=>-15=-3\(\sqrt{a}\)
<=>\(\sqrt{a}=5\)
<=>a=25(TM)
Vậy a=25 thì B=-3
c)Với \(a\ge0;a\ne16\) thì B=\(\dfrac{8}{\sqrt{a}-4}\)
Để B nguyên thì \(\dfrac{8}{\sqrt{a}-4}\)phải nguyên<=>8 chia hết cho \(\sqrt{a}-4\) <=>\(\sqrt{a}-4\)là Ư(8) Mà Ư(8)={-8;-4;-2;-1;1;2;4;8} Do \(\sqrt{a}\ge0\) ta có bảng sau:| \(\sqrt{a}-4\) | -8 | -4 | -2 | -1 | 1 | 2 | 4 | 8 |
| \(\sqrt{a}\) | -4(L) | 0 | 2 | 3 | 5 | 6 | 8 | 12 |
| \(\sqrt{a}\) | 0 | 2 | 3 | 5 | 6 | 8 | 12 |
| a | 0(TM) | 4(TM) | 9(TM) | 25(TM) | 36(TM) | 64(TM) | 144(TM) |
(BẠN KẺ 1 BẢNG 3 HÀNG THÔI NHA,MÌNH KẺ LỖI NÊN LÀM 2 BẢNG)
Vậy...
Đúng 0
Bình luận (2)
Cho hình tứ diện ABCD.
a) Chứng minh rằng:
B) Từ đẳng thức trên hãy suy ra rằng nếu tứ diện ABCD có AB ⊥ CD và AC ⊥ DB thì AD ⊥ BC.
Đọc tiếp
Cho hình tứ diện ABCD.
a) Chứng minh rằng:
B) Từ đẳng thức trên hãy suy ra rằng nếu tứ diện ABCD có AB ⊥ CD và AC ⊥ DB thì AD ⊥ BC.
a)
Cộng từng vế ba đẳng thức trên ta được đpcm.
b) AB ⊥ CD =>
AC ⊥ DB => =>
=> AD ⊥ BC.
Đúng 0
Bình luận (0)
Trong không gian cho hai hình vuông ABCD và ABC'D' có chung cạnh AB và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm O và O'. Chứng minh rằng AB ⊥ OO' và tứ giác CDD'C' là hình chữ nhật.
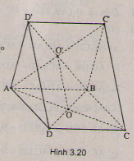
= AB.AO'.cos - AB.AO.cos
= 0.
Vậy AB ⊥ OO'.
Đúng 0
Bình luận (1)
Cho tứ diện ABCD có AB AC AD và Chứng minh rằng:
a) AB ⊥ CD;
b) Nếu M, N lần lượt là trung điểm của AB và CD thì MN ⊥ AB và MN ⊥ CD.
Đọc tiếp
Cho tứ diện ABCD có AB = AC = AD và Chứng minh rằng:
a) AB ⊥ CD;
b) Nếu M, N lần lượt là trung điểm của AB và CD thì MN ⊥ AB và MN ⊥ CD.
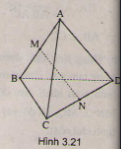
a)
Suy ra
Ta có => AB ⊥ MN.
Chứng minh tương tự được CD ⊥ MN.
Đúng 0
Bình luận (0)
tính số đo góc x,y trong hình sau;
a b d x y c
biết 2x3y
hình b
A B E C D X X 120 độ
ai nhanh và đúng mk tick cho
Đọc tiếp
tính số đo góc x,y trong hình sau;
biết 2x=3y
hình b
ai nhanh và đúng mk tick cho
Câu 1. Cho hàm số y = x³ – 3x có đồ thị (C). Tìm số giao điểm của (C) và trục hoành.
Ta có:
y = 0 \(\Leftrightarrow\)x3-3x = 0 \(\Leftrightarrow\) x = 0,x = \(\pm\)\(\sqrt{3}\).
Do đó số giao điểm (C) và trục hoành là 3.
Đúng 0
Bình luận (0)











