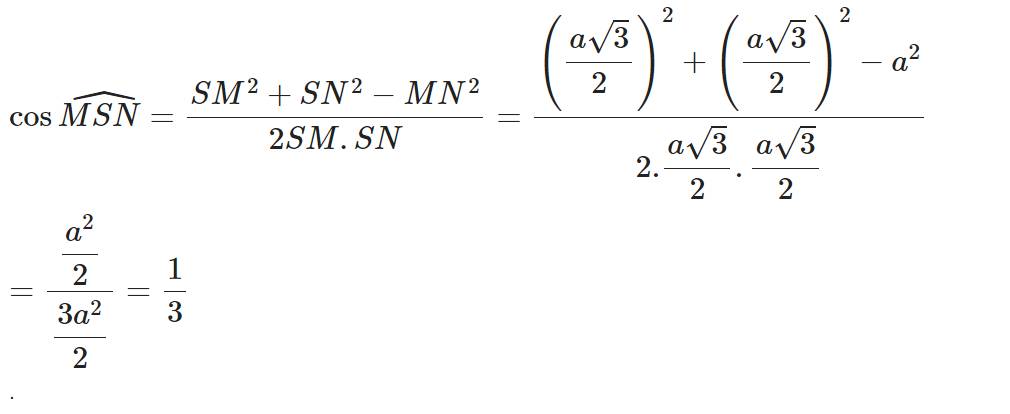Cho S.ABC có SA,SB,SC đôi một vuông góc. Biết rằng SA=SB= a, SC =\(a\sqrt{2}\). Hỏi góc giữa (SBC) và (ABC)?
Bài 6: Ôn tập chương Vecơ trong không gian. Quan hệ vuông góc trong không gian.
Cho chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và (SCD) tạo với mặt phẳng đáy góc 45°. Tính góc giữa (SBC) và (SCD).
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a . Tính cosin của góc giữa hai mặt bên không liền kề nhau
Cho S.ABCD có đáy là hình chữ nhật, AB=a,SA vuông góc mặt phẳng đáy, SC hợp với mặt phẳng đáy góc 45° và hợp với (SAB) góc 30. Tính góc giữa (SBC) và mặt phẳng đáy?
Cho hình chóp S.ABCD có mặt phẳng đáy hình thoi cạnh a, ABC =60°, SA vuông góc mặt phẳng đáy là SA=\(a\sqrt{3}\). Tính góc giữa (SBC) và (ABCD) ?
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính cosin của góc giữa hai mặt bên liền kề nhau.
Cho tam giác cân ABC có đường cao AH asqrt{3}, mặt phẳng đáy BC 3a, BC ⊂(P), A∉(P) . Gọi A là hình chiếu vuông góc của A lên (P). Tam giác ABC vuông tại A. Gọi α là góc giữa (P) và (ABC). Tính α
Đọc tiếp
Cho tam giác cân ABC có đường cao AH = \(a\sqrt{3}\), mặt phẳng đáy BC = 3a, BC ⊂(P), A∉(P) . Gọi A' là hình chiếu vuông góc của A lên (P). Tam giác A'BC vuông tại A'. Gọi α là góc giữa (P) và (ABC). Tính α
Cho tam giác đều ABC cạnh a. dB, dc lần lượt là đường thẳng đi qua B, C và vuông góc (ABC). (P) là mặt phẳng đi qua A và hợp với (ABC) một góc bằng 60°. (P) cắt dB, dc tại D và E.ADdfrac{asqrt{6}}{2};AEasqrt{3}. Đặt β DAE. Khẳng định nào sau đây đúng, vì sao?A. 30oB. sinβ dfrac{2}{sqrt{6}}C. sinβ dfrac{sqrt{6}}{2}D. β 60o
Đọc tiếp
Cho tam giác đều ABC cạnh a. dB, dc lần lượt là đường thẳng đi qua B, C và vuông góc (ABC). (P) là mặt phẳng đi qua A và hợp với (ABC) một góc bằng 60°. (P) cắt dB, dc tại D và E.
AD=\(\dfrac{a\sqrt{6}}{2}\);AE=\(a\sqrt{3}\). Đặt β = DAE. Khẳng định nào sau đây đúng, vì sao?
A. 30o
B. sinβ = \(\dfrac{2}{\sqrt{6}}\)
C. sinβ = \(\dfrac{\sqrt{6}}{2}\)
D. β = 60o
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Gọi E là trung điểm cạnh S. Tính cosin của góc giữa hai mặt phẳng (SBD) và (EBD).
Cho chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB=4a, AD=3a. Các cạnh bên đều có độ dài 5a. Tính góc giữa (SBC) và (ABCD) ?