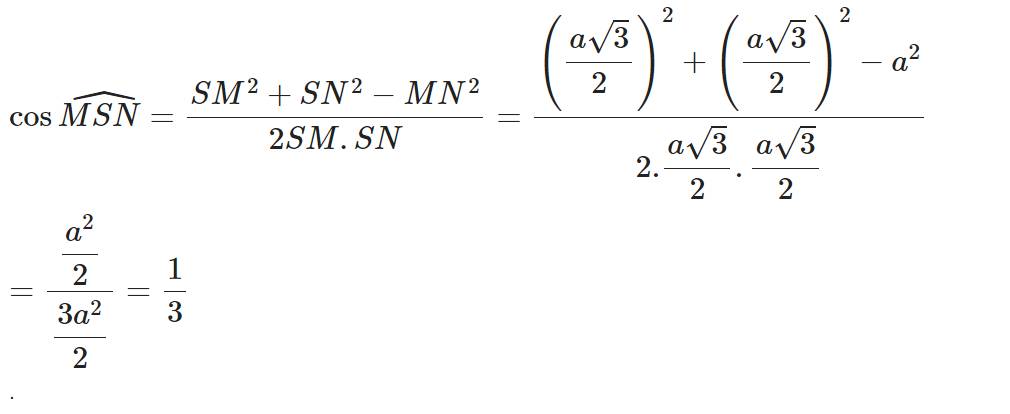Bài 6: Ôn tập chương Vecơ trong không gian. Quan hệ vuông góc trong không gian.
Các câu hỏi tương tự
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính cosin của góc giữa hai mặt bên liền kề nhau.
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Gọi E là trung điểm cạnh S. Tính cosin của góc giữa hai mặt phẳng (SBD) và (EBD).
Cho chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB=4a, AD=3a. Các cạnh bên đều có độ dài 5a. Tính góc giữa (SBC) và (ABCD) ?
Câu 5: Cho hình chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông tâm O cạnh bằng a, góc giữa cạnh bên và mặt đáy 1 góc 60°. Gọi IE lần lượt là là trung điểm của cạnh BC,CD a)Chứng minh: AC vuông góc (SBD) ; BD vuông góc SA b)Chứng minh: (SBC) vuông góc (SOI) c)Tính góc giữa mặt bên và mặt đáy. d)góc giữa OE và mặt (SCD) e)Tính khoảng cách giữa SI và AB.
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a tất cả các cạnh bên đều bằng a. Gọi điểmM thuộc SD sao cho SD =3SM, G là trọng tâm của tam giác BCD gọi (a) là mặt phẳng chứa MG và song song với CD. Xác định và tính diện tích thiết diện của hình chóp với mp (a)
Xem chi tiết
Hình chóp tam giác S.ABC có đáy là tam giác đều ABC cạnh 7a, có cạnh SC vuông góc với mặt phẳng đáy (ABC) và SC = 7a
a) Tính góc giữa SA và BC
b) Tính khoảng cách giữa hai đường thẳng chéo nhau SA và BC
Cho hình chóp S. ABCD có đáy là hình thoi cạnh a, Góc ABC =120°, SA vuông góc với mặt đáy. Biết góc giữa hai mặt phẳng (SBC) và (SCD) bằng 60. Tính SA Mọi người giúp em với ạ!!!!
Hình chóp A.ABCD có đáy là hình vuông ABCD cạnh a, cạnh SA bằng a và vuông góc với mặt phẳng (ABCD)
a) Chứng minh rằng các mặt bên kia của hình chóp là những tam giác vuông
b) Mặt phẳng \(\left(\alpha\right)\) đi qua A và vuông góc với cạnh SC lần lượt cắt SB, SC, SD tại B', C', D'. Chứng minh B'D' song song với BD và AB' vuông góc với SB
Trên mặt phẳng left(alpharight) cho hình vuông ABCD. Các tia Ax, By, Cz, Dt vuông góc với mặt phẳng left(alpharight) và nằm về một phía đối với mặt phẳng left(alpharight) . Một mặt phẳng left(betaright) lần lượt cắt Ax,By,Cz,Dt tại A, B, C, D.
a) Tứ giác ABCD là hình gì ? Chứng minh rằng AA + CCBB+DD
b) Chứng minh rằng điều kiện để tứ giác ABCD là hình thoi là nó có hai đỉnh đối diện cách đều mặt phẳng left(alpharight)
c) Chứng minh rằng điều kiện để tứ giác ABCD là hình chữ nhật là nó có hai...
Đọc tiếp
Trên mặt phẳng \(\left(\alpha\right)\) cho hình vuông ABCD. Các tia Ax, By, Cz, Dt vuông góc với mặt phẳng \(\left(\alpha\right)\) và nằm về một phía đối với mặt phẳng \(\left(\alpha\right)\) . Một mặt phẳng \(\left(\beta\right)\) lần lượt cắt \(Ax,By,Cz,Dt\) tại A', B', C', D'.
a) Tứ giác A'B'C'D' là hình gì ? Chứng minh rằng AA' + CC'=BB'+DD'
b) Chứng minh rằng điều kiện để tứ giác A'B'C'D' là hình thoi là nó có hai đỉnh đối diện cách đều mặt phẳng \(\left(\alpha\right)\)
c) Chứng minh rằng điều kiện để tứ giác A'B'C'D' là hình chữ nhật là nó có hai đỉnh kề nhau cách đều mặt phẳng \(\left(\alpha\right)\)