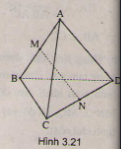
a)
Suy ra
Ta có => AB ⊥ MN.
Chứng minh tương tự được CD ⊥ MN.
Đúng 0
Bình luận (0)
Bài 6: Ôn tập chương Vecơ trong không gian. Quan hệ vuông góc trong không gian.
Các câu hỏi tương tự
Cho tứ diện ABCD với AB a, CD b, AC c. Lấy M là điểm bất kì trên đoạn AC. Qua M ta vẽ một mặt phẳng (P) song song với hai cạnh AB và CD. Gọi M, N, R, S lần lượt là giao điểm của (P) với các cạnh AC, BC, BD, AD
a) Tìm điều kiện để MNRS là hình chữ nhật
b) Đặt AM x, (0 x c). Tìm diện tích S của tứ giác MNRS khi ABperp CD. Tìm giá trị lớn nhất của S ?
Đọc tiếp
Cho tứ diện ABCD với AB = a, CD = b, AC = c. Lấy M là điểm bất kì trên đoạn AC. Qua M ta vẽ một mặt phẳng (P) song song với hai cạnh AB và CD. Gọi M, N, R, S lần lượt là giao điểm của (P) với các cạnh AC, BC, BD, AD
a) Tìm điều kiện để MNRS là hình chữ nhật
b) Đặt AM = x, (0 < x < c). Tìm diện tích S của tứ giác MNRS khi \(AB\perp CD\). Tìm giá trị lớn nhất của S ?
Cho tứ diện ABCD có \(AB\perp CD\) và AB = CD = AC = a. Trên đoạn AC lấy M với AM = x. Qua M ta vẽ mặt phẳng (P) song song với AB và CD. Mặt phẳng (P) cắt BC, BD, AD lần lượt tại N, R, T
a) Cho biết tính chất của tứ gác MNRT
b) Tìm diện tích S của tứ giác MNRT theo a và x. Tìm x để S lớn nhất
c) Tìm x để \(S=\dfrac{2a^2}{9}\)
Tứ diện ABCD có hai mặt ABC và ADC nằm trong hai mặt phẳng vuông góc với nhau. Tam giác ABC vuông tại A có AB = a, AC = b. Tam giác ADC vuông tại D có CD = a
a) Chứng minh các tam giác BAD và BDC là những tam giác vuông
b) Gọi I và K lần lượt là trung điểm của AD và BC. Chứng minh IK là đường vuông góc chung của hai đường thẳng AD và BC
Cho hình chóp S.ABCD, ABCD là hình chữ nhật. AB=a AD = a căn 3, SA =a. SA vuông góc với đáy. M,N lần lượt là trung điểm AD và SC. BM giao AC tại I
a) CM (SAC) vuông (SMB)
b) tính khoáng cách SB và CD. Tính diện tích tam giác NID
Cho hình chóp tứ giác đều S.ABCD. Gọi M, N lần lượt là trung điểm của SA và SC
a) Chứng minh \(AC\perp SD\)
b) Chứng minh \(MN\perp\left(SBD\right)\)
c) Cho AB = SA = a. Tính côsin của góc giữa (SBC) và (ABCD)
Cho tứ diện ABCD. Chứng minh rằng AB vuông góc với CD khi và chỉ khi :
\(AC^2+BD^2=AD^2+BC^2\)
Cho tứ diện ABCD có CD = 4/3 AB. Gọi I,J,K lần lược là trung điểm của BC, AC và BD. Cho biết JK = 5/6 AD. Tính góc giữ đường thẳng CD với các đường thẳng IJ và AB.
Giúp em với.!
Cho hai tia Ax và By vuông góc với nhau nhận AB làm đoạn vuông góc chung. Gọi M và N là hai điểm di động lần lượt trên Ax và By sao cho AM + BN MN
Đặt AB 2a, gọi O là trung điểm của AB và H là hình chiếu vuông góc của điểm O trên đường thẳng MN
a) Chứng minh rằng OH a, HM AM, HN BN
b) Gọi Bx là tia song song và cùng chiều với tia Ax và K là hình chiếu vuông góc của H trên mặt phẳng (Bx,By). Chứng minh BK là phân giác của góc xBy ?
c) Chứng minh điểm H nằm trên một đường tròn cố định ?
Đọc tiếp
Cho hai tia Ax và By vuông góc với nhau nhận AB làm đoạn vuông góc chung. Gọi M và N là hai điểm di động lần lượt trên Ax và By sao cho AM + BN = MN
Đặt AB = 2a, gọi O là trung điểm của AB và H là hình chiếu vuông góc của điểm O trên đường thẳng MN
a) Chứng minh rằng OH = a, HM = AM, HN = BN
b) Gọi Bx' là tia song song và cùng chiều với tia Ax và K là hình chiếu vuông góc của H trên mặt phẳng (Bx',By). Chứng minh BK là phân giác của góc x'By ?
c) Chứng minh điểm H nằm trên một đường tròn cố định ?
Câu 5: Cho hình chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông tâm O cạnh bằng a, góc giữa cạnh bên và mặt đáy 1 góc 60°. Gọi IE lần lượt là là trung điểm của cạnh BC,CD a)Chứng minh: AC vuông góc (SBD) ; BD vuông góc SA b)Chứng minh: (SBC) vuông góc (SOI) c)Tính góc giữa mặt bên và mặt đáy. d)góc giữa OE và mặt (SCD) e)Tính khoảng cách giữa SI và AB.