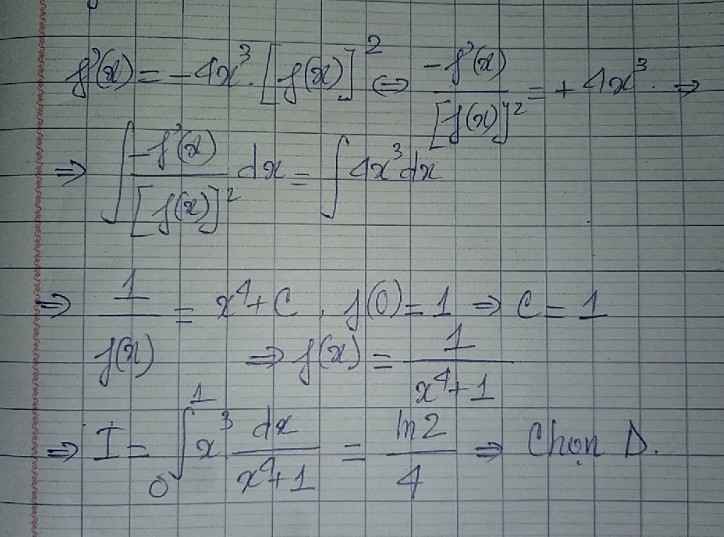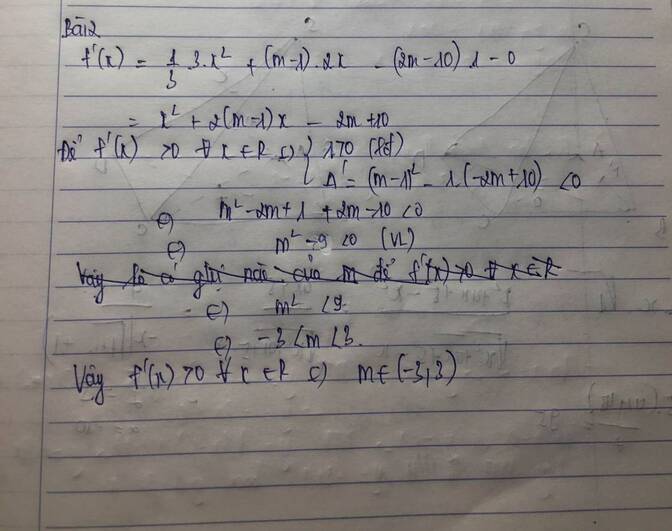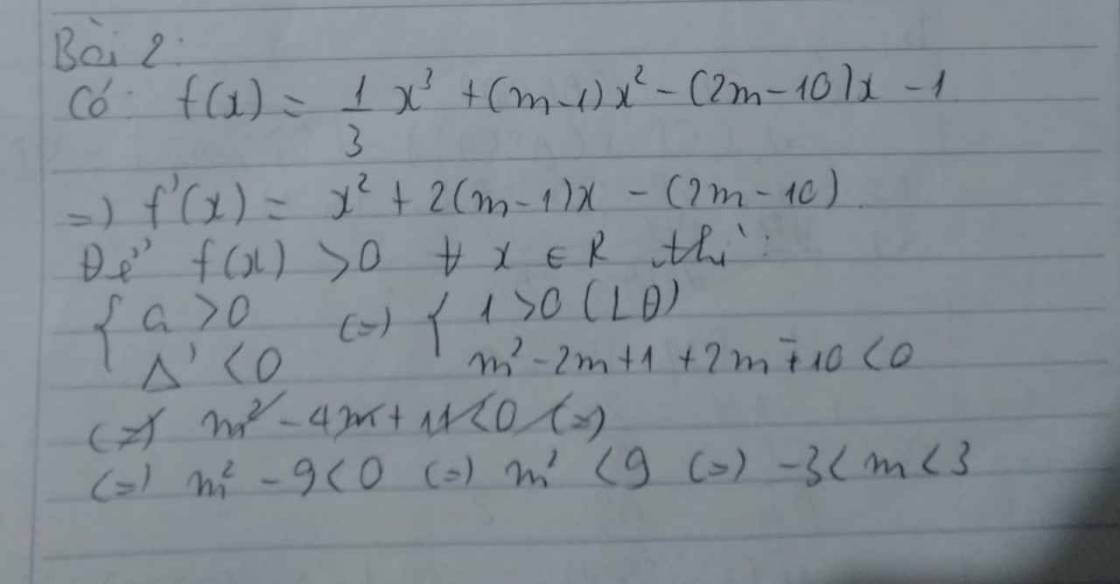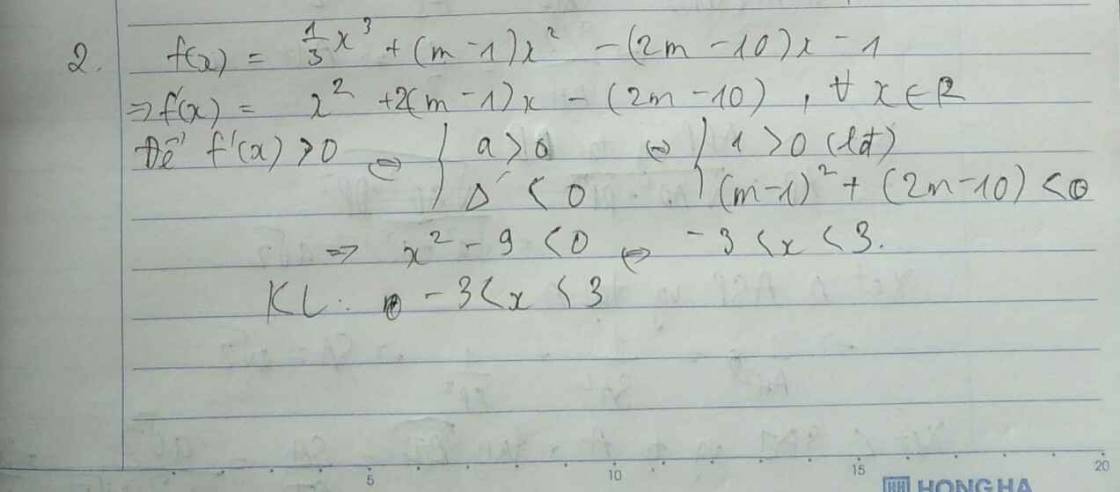Cho \(A=\left\{x\in R|\left(x+1\right)^2+\left(x-1\right)^2=10\right\};B=\left\{x\in R|\left(x+1\right)^4+\left(x-1\right)^4=82\right\}\)Tìm tập X sao cho A\(\cup\)X=B.

Những câu hỏi liên quan
Cho các tập hợp sau A= \(\left\{x\in R|\left(x-2x^2\right)\left(x^2-3x+2\right)=0\right\}\) và B=\(\left\{n\in N|3< n\left(n+1\right)< 31\right\}\)
Tìm A \(\cap\) B
\(A=\left\{x\in R|\left(x-2x^2\right)\left(x^2-3x+2\right)=0\right\}\)
Giải phương trình sau :
\(\left(x-2x^2\right)\left(x^2-3x+2\right)=0\)
\(\Leftrightarrow x\left(1-2x\right)\left(x-1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\1-2x=0\\x-1=0\\x-2=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\\x=1\\x=2\end{matrix}\right.\)
\(\Rightarrow A=\left\{0;\dfrac{1}{2};1;2\right\}\)
\(B=\left\{n\in N|3< n\left(n+1\right)< 31\right\}\)
Giải bất phương trình sau :
\(3< n\left(n+1\right)< 31\)
\(\Leftrightarrow\left\{{}\begin{matrix}n\left(n+1\right)>3\\n\left(n+1\right)< 31\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}n^2+n-3>0\\n^2+n-31< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}n< \dfrac{-1-\sqrt[]{13}}{2}\cup n>\dfrac{-1+\sqrt[]{13}}{2}\\\dfrac{-1-5\sqrt[]{5}}{2}< n< \dfrac{-1+5\sqrt[]{5}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{-1-5\sqrt[]{5}}{2}< n< \dfrac{-1-\sqrt[]{13}}{2}\\\dfrac{-1+\sqrt[]{13}}{2}< n< \dfrac{-1+5\sqrt[]{5}}{2}\end{matrix}\right.\)
Vậy \(B=\left(\dfrac{-1-5\sqrt[]{5}}{2};\dfrac{-1-\sqrt[]{13}}{2}\right)\cup\left(\dfrac{-1+\sqrt[]{13}}{2};\dfrac{-1+5\sqrt[]{5}}{2}\right)\)
\(\Rightarrow A\cap B=\left\{2\right\}\)
Đúng 1
Bình luận (0)
Cho f(x) là hàm đa thức thỏa \(\lim\limits_{x\rightarrow2}\dfrac{f\left(x\right)+1}{x-2}=a\left(a\in R\right)\) và tồn tại \(\lim\limits_{x\rightarrow2}\dfrac{\sqrt{f\left(x\right)+2x+1}-x}{x^2-4}=T\left(T\in R\right).\) Tìm T theo a.
\(\lim\limits_{x\rightarrow2}\dfrac{f\left(x\right)+1}{x-2}\) hữu hạn \(\Rightarrow f\left(x\right)+1=0\) có nghiệm \(x=2\Rightarrow f\left(2\right)=-1\)
\(\lim\limits_{x\rightarrow2}\dfrac{\sqrt{f\left(x\right)+2x+1}-x}{x^2-4}=\lim\limits_{x\rightarrow2}\dfrac{1}{\sqrt{f\left(x\right)+2x+1}+x}.\dfrac{\left(\sqrt{f\left(x\right)+2x+1}-x\right)\left(\sqrt{f\left(x\right)+2x+1}+x\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{1}{\left(x+2\right)\left(\sqrt{f\left(x\right)+2x+1}+x\right)}.\dfrac{f\left(x\right)+1-x\left(x-2\right)}{x-2}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{1}{\left(x+2\right)\left(\sqrt{f\left(x\right)+2x+1}+x\right)}.\left(\lim\limits_{x\rightarrow2}\dfrac{f\left(x\right)+1}{x-2}-\lim\limits_{x\rightarrow2}\dfrac{x\left(x-2\right)}{x-2}\right)\)
\(=\dfrac{1}{4\left(\sqrt{4}+2\right)}.\left(a-2\right)=\dfrac{a-2}{16}\)
Đúng 1
Bình luận (0)
Cho hàm số \(y=f\left(x\right)\) có đạo hàm \(f'\left(x\right)=\left(x-2\right)^2\left(x-1\right)\left(x^2-2\left(m+1\right)x+m^2-1\right)\) , \(\forall x\in R\) . Có bao nhiêu giá trị nguyên của m để hàm số \(g\left(x\right)=f\left(\left|x\right|\right)\) có 5 điểm cực trị ?
đi từ hướng làm để ra được bài toán:
Ta thấy muốn f(|x|) có 5 điểm cực trị thì f'(x) phải có 2 điểm cực trị dương
giải f'(x)=0 \(\left\{{}\begin{matrix}x=1\\x^2-2\left(m+1\right)x+m^2-1=0\left(2\right)\end{matrix}\right.\) phương trình (2) phải có 2 nghiệm phân biệt trái dấu nhau
Ta có: \(\Delta>0\Leftrightarrow m>-1\)
Theo yêu cầu bài toán: \(m^2-1>0\Leftrightarrow\left[{}\begin{matrix}m< -1\\m>1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Viết mỗi tập hợp sau bằng cách liệt kê các phần tử:a) A { xin R | left(2x^2-5x+3right)left(x^2-4x+3right)0 }b) B { xin R | left(x^2-10x+21right)left(x^3-xright)0 }c) C { xin R | left(6x^2-7x+1right)left(x^2-5x+6right) 0 }d) D { xin Z | 2x^2-5x+30 }e) E { xin N | left{{}begin{matrix}x+3 4+2x5x-3 4x-1end{matrix}right. }f) F { xin Z | left|x+2right|le1 }g) G { xin N | x 5 }h) H { xin R | x^2+x+30 }
Đọc tiếp
Viết mỗi tập hợp sau bằng cách liệt kê các phần tử:
a) A = { \(x\in R\) | \(\left(2x^2-5x+3\right)\left(x^2-4x+3\right)=0\) }
b) B = { \(x\in R\) | \(\left(x^2-10x+21\right)\left(x^3-x\right)=0\) }
c) C = { \(x\in R\) | \(\left(6x^2-7x+1\right)\left(x^2-5x+6\right)\) = 0 }
d) D = { \(x\in Z\) | \(2x^2-5x+3=0\) }
e) E = { \(x\in N\) | \(\left\{{}\begin{matrix}x+3< 4+2x\\5x-3< 4x-1\end{matrix}\right.\) }
f) F = { \(x\in Z\) | \(\left|x+2\right|\le1\) }
g) G = { \(x\in N\) | x < 5 }
h) H = { \(x\in R\) | \(x^2+x+3=0\) }
`a)(2x^2-5x+3)(x^2-4x+3)=0`
`<=>[(2x^2-5x+3=0),(x^2-4x+3=0):}<=>[(x=3/2),(x=1),(x=3):}`
`=>A={3/2;1;3}`
`b)(x^2-10x+21)(x^3-x)=0`
`<=>[(x^2-10x+21=0),(x^3-x=0):}<=>[(x=7),(x=3),(x=0),(x=+-1):}`
`=>B={0;+-1;3;7}`
`c)(6x^2-7x+1)(x^2-5x+6)=0`
`<=>[(6x^2-7x+1=0),(x^2-5x+6=0):}<=>[(x=1),(x=1/6),(x=2),(x=3):}`
`=>C={1;1/6;2;3}`
`d)2x^2-5x+3=0<=>[(x=1),(x=3/2):}` Mà `x in Z`
`=>D={1}`
`e){(x+3 < 4+2x),(5x-3 < 4x-1):}<=>{(x > -1),(x < 2):}<=>-1 < x < 2`
Mà `x in N`
`=>E={0;1}`
`f)|x+2| <= 1<=>-1 <= x+2 <= 1<=>-3 <= x <= -1`
Mà `x in Z`
`=>F={-3;-2;-1}`
`g)x < 5` Mà `x in N`
`=>G={0;1;2;3;4}`
`h)x^2+x+3=0` (Vô nghiệm)
`=>H=\emptyset`.
Đúng 2
Bình luận (0)
Cho Eleft{xin Z|left|xright|le5right}; Aleft{xin R|x^2+3x-40right};Bleft{xin Z|(x-2)(x+1)(2x^2-x-3)0right}a) CM Asubset E,Bsubset Eb) Tìm Ebackslashleft(Acap Bright),Ebackslashleft(Acup Bright) rồi tìm quan hệ giữa hai tập hợp này.
Đọc tiếp
Cho \(E=\left\{x\in Z|\left|x\right|\le5\right\}\); \(A=\left\{x\in R|x^2+3x-4=0\right\}\);
\(B=\left\{x\in Z|(x-2)(x+1)(2x^2-x-3)=0\right\}\)
a) CM \(A\subset E\),\(B\subset E\)
b) Tìm \(E\backslash\left(A\cap B\right)\),\(E\backslash\left(A\cup B\right)\) rồi tìm quan hệ giữa hai tập hợp này.
\(E=\left\{-5;-4;-3;-2;-1;0;1;2;3;4;5\right\}\)
\(A=\left\{1;-4\right\}\)
\(B=\left\{2;-1\right\}\)
a) Với mọi x thuộc A đều thuộc E \(\Rightarrow A\subset E\)
Với mọi x thuộc B đều thuộc E \(\Rightarrow B\subset E\)
b) \(A\cap B=\varnothing\)
\(\Rightarrow E\backslash\left(A\cap B\right)=\left\{-5;-4;-3;-2;-1;0;1;2;3;4;5\right\}\)
\(A\cup B=\left\{-4;-1;1;2\right\}\)
\(\Rightarrow E\backslash\left(A\cup B\right)=\left\{-5;-3;-2;0;3;4;5\right\}\)
\(\Rightarrow E\backslash\left(A\cup B\right)\subset E\backslash\left(A\cap B\right)\)
Đúng 2
Bình luận (0)
Cho \(A=\left\{x\in R/\frac{1}{\left|x-2\right|}>2\right\}\);\(B=\left\{x\in R/\left|x-1\right|< 1\right\}\).Hãy tìm \(A\cup B,A\B\)
\(\frac{1}{\left|x-2\right|}>2\Rightarrow\left|x-2\right|< \frac{1}{2}\Rightarrow-\frac{1}{2}< x-2< \frac{1}{2}\)
\(\Rightarrow\frac{3}{2}< x< \frac{5}{2}\)
\(\Rightarrow A=\left(\frac{3}{2};\frac{5}{2}\right)\)
\(\left|x-1\right|< 1\Rightarrow-1< x-1< 1\Rightarrow0< x< 2\)
\(\Rightarrow B=\left(0;2\right)\)
\(\Rightarrow A\cup B=\left(0;\frac{5}{2}\right)\)
\(A\backslash B=[2;\frac{5}{2})\)
Đúng 0
Bình luận (0)
1. Có bao nhiêu min Z inleft[-30;40right] để bpt sau đúng forall xin Ra.left(x+1right)left(x-2right)left(x+2right)left(x+5right)ge mb.b.left(x^2-2x+4right)left(x^2+3x+4right)ge mx^22. Tìm m để ptleft(m+3right)x-2sqrt{x^2-1}+m-30 có nghiệm xge1
Đọc tiếp
1. Có bao nhiêu \(m\in Z\) \(\in\left[-30;40\right]\) để bpt sau đúng \(\forall x\in R\)
\(a.\left(x+1\right)\left(x-2\right)\left(x+2\right)\left(x+5\right)\ge m\)
b.\(b.\left(x^2-2x+4\right)\left(x^2+3x+4\right)\ge mx^2\)
2. Tìm m để pt
\(\left(m+3\right)x-2\sqrt{x^2-1}+m-3=0\) có nghiệm \(x\ge1\)
1.a.
\(\left(x+1\right)\left(x+2\right)\left(x-2\right)\left(x+5\right)\ge m\)
\(\Leftrightarrow\left(x^2+3x+2\right)\left(x^2+3x-10\right)\ge m\)
Đặt \(x^2+3x-10=t\ge-\dfrac{49}{4}\)
\(\Rightarrow\left(t+2\right)t\ge m\Leftrightarrow t^2+2t\ge m\)
Xét \(f\left(t\right)=t^2+2t\) với \(t\ge-\dfrac{49}{4}\)
\(-\dfrac{b}{2a}=-1\) ; \(f\left(-1\right)=-1\) ; \(f\left(-\dfrac{49}{4}\right)=\dfrac{2009}{16}\)
\(\Rightarrow f\left(t\right)\ge-1\)
\(\Rightarrow\) BPT đúng với mọi x khi \(m\le-1\)
Có 30 giá trị nguyên của m
Đúng 2
Bình luận (0)
1b.
Với \(x=0\) BPT luôn đúng
Với \(x\ne0\) BPT tương đương:
\(\dfrac{\left(x^2-2x+4\right)\left(x^2+3x+4\right)}{x^2}\ge m\)
\(\Leftrightarrow\left(x+\dfrac{4}{x}-2\right)\left(x+\dfrac{4}{x}+3\right)\ge m\)
Đặt \(x+\dfrac{4}{x}-2=t\) \(\Rightarrow\left[{}\begin{matrix}t\ge2\\t\le-6\end{matrix}\right.\)
\(\Rightarrow t\left(t+5\right)\ge m\Leftrightarrow t^2+5t\ge m\)
Xét hàm \(f\left(t\right)=t^2+5t\) trên \(D=(-\infty;-6]\cup[2;+\infty)\)
\(-\dfrac{b}{2a}=-\dfrac{5}{2}\notin D\) ; \(f\left(-6\right)=6\) ; \(f\left(2\right)=14\)
\(\Rightarrow f\left(t\right)\ge6\)
\(\Rightarrow m\le6\)
Vậy có 37 giá trị nguyên của m thỏa mãn
Đúng 2
Bình luận (0)
2.
Xét với \(x\ge1\)
\(m\left(x+1\right)+3\left(x-1\right)-2\sqrt{x^2-1}=0\)
\(\Leftrightarrow m+3\left(\dfrac{x-1}{x+1}\right)-2\sqrt{\dfrac{x-1}{x+1}}=0\)
Đặt \(\sqrt{\dfrac{x-1}{x+1}}=t\Rightarrow0\le t< 1\)
\(\Rightarrow m+3t^2-2t=0\)
\(\Leftrightarrow3t^2-2t=-m\)
Xét hàm \(f\left(t\right)=3t^2-2t\) trên \(D=[0;1)\)
\(-\dfrac{b}{2a}=\dfrac{1}{3}\in D\) ; \(f\left(0\right)=0\) ; \(f\left(\dfrac{1}{3}\right)=-\dfrac{1}{3}\) ; \(f\left(1\right)=1\)
\(\Rightarrow-\dfrac{1}{3}\le f\left(t\right)< 1\)
\(\Rightarrow\) Pt có nghiệm khi \(-\dfrac{1}{3}\le-m< 1\)
\(\Leftrightarrow-1< m\le\dfrac{1}{3}\)
Đúng 2
Bình luận (0)
Cho hàm số fleft(xright) có đạo hàm fleft(xright) liên tục trên R và thỏa mãn các điều kiện fleft(xright)0,forall xin R, fleft(0right)1 và fleft(xright)-4x^3.left(fleft(xright)right)^2,forall xin R. Tính Iint_0^1x^3fleft(xright)dxA.Idfrac{1}{6} B. Iln2 C. Idfrac{1}{4} D. Idfrac{ln2}{4}Mình cần bài giải ạ, mình cảm ơn nhiều♥
Đọc tiếp
Cho hàm số \(f\left(x\right)\) có đạo hàm \(f'\left(x\right)\) liên tục trên \(R\) và thỏa mãn các điều kiện \(f\left(x\right)>0,\forall x\in R\), \(f\left(0\right)=1\) và \(f'\left(x\right)=-4x^3.\left(f\left(x\right)\right)^2,\forall x\in R\). Tính \(I=\int_0^1x^3f\left(x\right)dx\)
A.\(I=\dfrac{1}{6}\) B. \(I=ln2\) C. \(I=\dfrac{1}{4}\) D. \(I=\dfrac{ln2}{4}\)
Mình cần bài giải ạ, mình cảm ơn nhiều♥

\(f'\left(x\right)=-4x^3\left(f\left(x\right)\right)^2\Leftrightarrow-\dfrac{f'\left(x\right)}{\left(f\left(x\right)\right)^2}=4x^3\)
Lấy nguyên hàm hai vế
\(\int-\dfrac{f'\left(x\right)}{\left(f\left(x\right)\right)^2}dx=\int4x^3dx\)
\(\Leftrightarrow\dfrac{1}{f\left(x\right)}=x^4+c\)
Thay x=0 vào tìm được c=1 \(\Rightarrow f\left(x\right)=\dfrac{1}{x^4+1}\)
\(I=\int\limits^1_0\dfrac{x^3}{x^4+1}dx=\dfrac{1}{4}\int\limits^1_0\dfrac{\left(x^4+1\right)'}{x^4+1}dx=\dfrac{ln2}{4}\)
Chọn D
Đúng 1
Bình luận (0)
Cho biểu thức $f\left( x \right)=\dfrac{1}{3}{{x}^{3}}+\left( m-1 \right){{x}^{2}}-\left( 2m-10 \right)x-1$ với $m$ là tham số thực. Tìm tất cả các giá trị của $m$ để ${f}'\left( x \right)>0$ $\forall x\in \mathbb{R}$.
Xem thêm câu trả lời