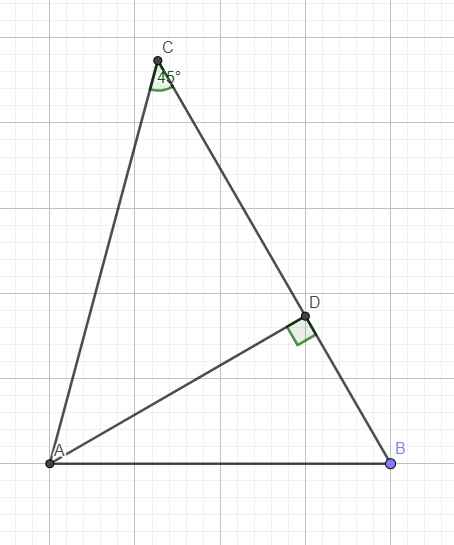
Cho tam giác ABC có góc C bằng 45 độ, AB. AC=32\(\sqrt{6}\), AB:AC=\(\sqrt{6}\):3. Tính BC, góc B và diện tích tam giác ABC
\(\dfrac{AB}{AC}=\dfrac{\sqrt{6}}{3}\Rightarrow AB=\dfrac{AC\sqrt{6}}{3}\)
\(AB.AC=32\sqrt{6}\Rightarrow\dfrac{AC^2\sqrt{6}}{3}=32\sqrt{6}\)
\(\Rightarrow AC^2=96\Rightarrow AC=4\sqrt{6}\)
\(\Rightarrow AB=\dfrac{AC\sqrt{6}}{3}=8\)
Kẻ đường cao AD ứng với BC
Do \(C=45^0\Rightarrow\widehat{CAD}=90^0-45^0=45^0\Rightarrow\Delta ACD\) vuông cân tại D
\(\Rightarrow AD=CD=\dfrac{AC}{\sqrt{2}}=4\sqrt{3}\)
Pitago tam giác vuông ABD:
\(BD=\sqrt{AB^2-AD^2}=4\)
\(\Rightarrow BC=CD+BD=4+4\sqrt{3}\)
\(cosB=\dfrac{BD}{AB}=\dfrac{4}{8}=\dfrac{1}{2}\Rightarrow B=60^0\)
\(S_{ABC}=\dfrac{1}{2}AD.BC=\dfrac{1}{2}.4\sqrt{3}.\left(4+4\sqrt{3}\right)=...\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có BC = \(\sqrt{6}\) , AC = 2 và AB = \(\sqrt{3}+1\) và . Bán kính đường tròn ngoại tiếp tam giác ABC bằng:
Lời giải:
$p=\frac{AB+BC+AC}{2}=\frac{\sqrt{6}+\sqrt{3}+3}{2}$
Theo công thức Heron:
$S_{ABC}=\sqrt{p(p-AB)(p-BC)(p-AC)}=\frac{3+\sqrt{3}}{2}$
Bán kính đường tròn ngoại tiếp:
$R=\frac{AB.BC.AC}{4S}=\sqrt{2}$ (đvđd)
Đúng 3
Bình luận (0)
Cho tam giác ABC đều có A(2; 0) phương trình BC: \(\sqrt{3}x-3y+6=0\). Viết phương trình các cạnh còn lại của tam giác ABC.
Đường thẳng BC nhận \(\overrightarrow{n}=\left(\sqrt{3};-3\right)\) là 1 vtpt
Gọi \(\overrightarrow{n_1}=\left(a;b\right)\) là 1 vtpt của AB (với a;b không đồng thời bằng 0)
Do tam giác ABC đều \(\Rightarrow\widehat{\left(n_1;\overrightarrow{n}\right)}=60^0\)
\(\Rightarrow cos\left(\overrightarrow{n_1};\overrightarrow{n}\right)=\dfrac{\left|a\sqrt{3}-3b\right|}{\sqrt{a^2+b^2}.\sqrt{3+9}}=\dfrac{1}{2}\)
\(\Leftrightarrow\left(a-\sqrt{3}b\right)^2=a^2+b^2\)
\(\Leftrightarrow a^2+3b^2-2\sqrt{3}ab=a^2+b^2\)
\(\Leftrightarrow b^2=\sqrt{3}ab\Rightarrow\left[{}\begin{matrix}b=0\\b=\sqrt{3}a\end{matrix}\right.\)
\(\Rightarrow\) Phương trình 2 cạnh còn lại có dạng:
\(\left\{{}\begin{matrix}a\left(x-2\right)+0\left(y-0\right)=0\\a\left(x-2\right)+\sqrt{3}a\left(y-0\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2=0\\x+\sqrt{3}y-2=0\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho tam giác ABC nhọn có: góc A bằng 60 độ; BC= \(\sqrt{\sqrt{3}-1}\)cm; diện tích tam giác ABC bằng \(\frac{\sqrt{3}}{6}\). Sin(B)+Sin(C)=\(\frac{\sqrt{6}+3\sqrt{2}}{4}\).Tính các góc B và C
tam giác ABC có AB=4,BC=6,AC=\(2\sqrt{7}\).Điểm M thuộc đoạn BC sao cho MC=2MB.Tính độ dài cạnh AM
Cho hình tứ diện SABC có đáy ABC là tam giác vuông tại B, có AB = a, BC =a\(\sqrt{5}\), SA vuông góc với (ABC), SA = a\(\sqrt{6}\)
a) Tính (SB;(ABC))
b) Tính (SA;(SBC))
a: (SB;(ABC))=(SB;BA)=góc SBA
\(\tan SBA=\dfrac{SA}{AB}=\sqrt{6}\)
=>góc SBA=68 độ
b: (SA;(SBC))=(SA;SB)=góc ASB
tan ASB=AB/SA=1/căn 6
=>góc ASB=22 độ
Đúng 0
Bình luận (0)
Cho tam giác ABC có \(a=6,b=4\sqrt{2},c=2\). M trên BC sao cho BM=2.
a,CosB=?
b,AM=?
Xét tam giác ABC có: BC2 = 62 = 36
AC2 + AB2 = (4√2)2 + 22 = 36
=> tam giác ABC vuông tại A (Py Ta Go đảo)
Sử dụng TSLG để tính góc B
Tính AM = BC - BM = 6 - 2 = 3 cm
Đúng 2
Bình luận (0)
BÀI NÁY NẰM TRONG HỆ THỨC LƯỢNG TAM GIÁC VUÔNG. Các bạn giúp mình với:Cho tam giác ABC vuông tại A, Đường cao AH, M là trung điểm của BC . Cho AB 2a. Tính các cạnh của tam giác ABCCho tam giác ABC vuông tại A. Điểm E,F thuộc cạnh AC vỚI AEEFFC và BE asqrt{3}, BFasqrt{6}. Tính các cạnh tam giác ABCCho tam giác ABC vuông tại A. hai đường trung tuyến AM và BN vuông góc nhau..Tính AB,BC nếu AC2a.Tính AB,AC nếu BC2aCho tam giác ABC vuông tại A, đường phân giác trong BE, EC 3, BC 6. TÍNH AB, AC
Đọc tiếp
BÀI NÁY NẰM TRONG HỆ THỨC LƯỢNG TAM GIÁC VUÔNG. Các bạn giúp mình với:
Cho tam giác ABC vuông tại A, Đường cao AH, M là trung điểm của BC . Cho AB =2a. Tính các cạnh của tam giác ABCCho tam giác ABC vuông tại A. Điểm E,F thuộc cạnh AC vỚI AE=EF=FC và BE= \(a\sqrt{3}\), BF=\(a\sqrt{6}\). Tính các cạnh tam giác ABCCho tam giác ABC vuông tại A. hai đường trung tuyến AM và BN vuông góc nhau..Tính AB,BC nếu AC=2a.Tính AB,AC nếu BC=2aCho tam giác ABC vuông tại A, đường phân giác trong BE, EC= 3, BC= 6. TÍNH AB, AC
Cho tam giác ABC, có góc B = 60 độ, góc C = 45 độ, BC = a.
a) Tính độ dài hai cạnh AB, AC.
b) Chứng minh cos 75 độ = \(\dfrac{\sqrt{6}-\sqrt{2}}{4}\)
a) Ta có:
\(\widehat{A}=180^o-60^o-45^o=75^o\)
Áp dụng định lý sin ta có:
\(\dfrac{BC}{sinA}=\dfrac{AC}{sinB}\)
\(\Rightarrow AC=\dfrac{BC\cdot sinB}{sinA}\)
\(\Rightarrow AC=\dfrac{a\cdot sin60^o}{sin75^o}=a\cdot\dfrac{3\sqrt{2}-\sqrt{6}}{2}\)
\(\dfrac{BC}{sinA}=\dfrac{AB}{sinC}\)
\(\Rightarrow AB=\dfrac{BC\cdot sinC}{sinA}\)
\(\Rightarrow AB=\dfrac{a\cdot sin45^o}{sin75^o}=a\cdot\left(\sqrt{3}-1\right)\)
b) \(cos75^o\)
\(=cos\left(30^o+45^o\right)\)
\(=cos30^o\cdot cos45^o-sin30^o\cdot sin45^o\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{2}-\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}\)
\(=\dfrac{\sqrt{2}}{2}\cdot\left(\dfrac{\sqrt{3}-1}{2}\right)\)
\(=\dfrac{\sqrt{6}-\sqrt{2}}{4}\left(dpcm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có I là giao điểm 3 đường phân giác của tam giác ABC.
a) Trong đó AB = 5 cm IC =6 cm.Tính BC
b)IB =\(\sqrt{5}\) IC =\(\sqrt{10}\) Tính AB, AC