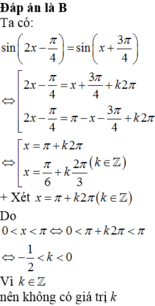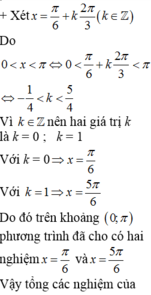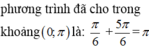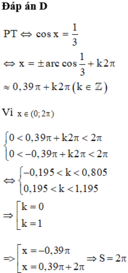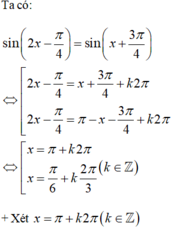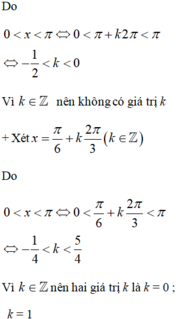Tính tổng các nghiệm thuộc \(\left[0;2\pi\right]\)thỏa mãn phương trình:
\(\left(sin\frac{x}{2}+cos\frac{x}{2}\right)^2+\sqrt{3}cosx=3\)

Những câu hỏi liên quan
Tính tổng tất cả các giá trị \(m\) nguyên để phương trình \(mcos2x=\dfrac{cos^4x-sin^4x}{sinx}\) có đúng 4 nghiệm phân biệt thuộc \(\left(0;2\pi\right)\).
A. 1
B. 2
C. 3
D. 0
Tổng các nghiệm thuộc \(\left(0;2\pi\right)\) của phương trình \(sinxcos3x-sinx+2cos3x-2=0\) là:
A. \(\dfrac{2\pi}{3}\)
B. \(2\pi\)
C. \(4\pi\)
D. 0
\(sinx.cos3x-sinx+2cos3x-2=0\)
\(\Leftrightarrow sinx\left(cos3x-1\right)+2\left(cos3x-1\right)=0\)
\(\Leftrightarrow\left(sinx+2\right)\left(cos3x-1\right)=0\)
\(\Leftrightarrow cos3x=1\)
\(\Leftrightarrow3x=k2\pi\)
\(\Rightarrow x=\dfrac{k2\pi}{3}\)
Do \(x\in\left(0;2\pi\right)\Rightarrow x=\left\{\dfrac{2\pi}{3};\dfrac{4\pi}{3}\right\}\)
\(\Rightarrow\dfrac{2\pi}{3}+\dfrac{4\pi}{3}=2\pi\)
Đúng 1
Bình luận (0)
Tính tổng các nghiệm thuộc khoảng
0
;
π
của phương trình
4
sin
2
x
2
-
3
cos
2
x
1
+
2
cos
2
x
-
3...
Đọc tiếp
Tính tổng các nghiệm thuộc khoảng 0 ; π của phương trình 4 sin 2 x 2 - 3 cos 2 x = 1 + 2 cos 2 x - 3 π 4
A. 37 π 18
B. π
C. 37 π 17
D. 3 π 2
Phương trình đã cho tương đương với
2 1 - cos x - 3 cos 2 x = 1 + 1 + cos 2 x - 3 π 2 ⇔ - 2 cos x = 3 cos 2 x - sin 2 x ⇔ - cos x = 3 2 cos 2 x - 1 2 sin 2 x ⇔ cos π - x = cos 2 x + π 6 ⇔ x = 5 π 18 + k 2 π 3 x = - 7 π 6 + k 2 π
Do x ∈ 0 ; π nên x ∈ 5 π 18 ; 17 π 18 ; 5 π 6 .
Vậy tổng các nghiệm là 37 π 18
Đáp án A
Đúng 0
Bình luận (0)
Tính tổng hợp tất cả các nghiệm thuộc khoảng
0
;
π
của phương trình:
2
cos
3
x
sin
x
+
cos
x
A.
π
B.
3
π
C.
3
π
2
D.
π
2
Đọc tiếp
Tính tổng hợp tất cả các nghiệm thuộc khoảng 0 ; π của phương trình: 2 cos 3 x = sin x + cos x
A. π
B. 3 π
C. 3 π 2
D. π 2
tính tổng các nghiệm của phương trình cos^4x-sin^4x=sin3x+cos4x thuộc đoạn [0;pi]
\(cos^4x-sin^4x=sin3x+cos4x\)
\(\Leftrightarrow\left(cos^2x+sin^2x\right)\left(cos^2x-sin^2x\right)=sin3x+cos4x\)
\(\Leftrightarrow cos2x=sin3x+cos4x\)
\(\Leftrightarrow cos4x-cos2x+sin3x=0\)
\(\Leftrightarrow-2sin3x.sinx+sin3x=0\)
\(\Leftrightarrow sin3x\left(1-2sinx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin3x=0\\sinx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{3}\\x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow x=\left\{0;\dfrac{\pi}{3};\dfrac{2\pi}{3};\pi;\dfrac{\pi}{6};\dfrac{5\pi}{6}\right\}\)
\(\Rightarrow\sum x=3\pi\)
Đúng 0
Bình luận (0)
Tính tổng S các nghiệm của phương trình \(\left(2cos2x+5\right)\left(sin^4x-cos^4x\right)+3=0\) trong khoảng \(\left(0;2\pi\right)\)
Cho phương trình
2
x
-
π
4
sin
x
+
3
π
4
. Tính tổng các nghiệm thuộc khoảng
0
;
π
của phương trình trên. A. ...
Đọc tiếp
Cho phương trình 2 x - π 4 = sin x + 3 π 4 . Tính tổng các nghiệm thuộc khoảng 0 ; π của phương trình trên.
A. 7 π 4
B. π
C. 3 π 2
D. π 4
Gọi S là tổng các nghiệm thuộc khoảng
0
,
2
π
của phương trình 3.cos x – 1 0. Tính S.
Đọc tiếp
Gọi S là tổng các nghiệm thuộc khoảng 0 , 2 π của phương trình 3.cos x – 1 = 0. Tính S.
![]()
![]()
![]()
![]()
Cho phương trình
2
x
-
π
4
sin
x
+
3
π
4
Tính tổng các nghiệm thuộc khoảng
0
;
π
của phương trình trên. A....
Đọc tiếp
Cho phương trình 2 x - π 4 = sin x + 3 π 4
Tính tổng các nghiệm thuộc khoảng 0 ; π của phương trình trên.
A. 7 π 2
B. π
C. 3 π 2
D. 4 π
Tính tổng tất cả các nghiệm thuộc [0;2022\(\pi\)] của phương trình \(\dfrac{3-cos2x+sin2x-5sinx-cosx}{2cosx+\sqrt{3}}=0\)
ĐKXĐ: \(cosx\ne-\dfrac{\sqrt{3}}{2}\) \(\Rightarrow\left[{}\begin{matrix}x\ne\dfrac{5\pi}{6}+k2\pi\\x\ne\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\)
\(pt\Rightarrow3-\left(1-2sin^2x\right)+2sinx.cosx-5sinx-cosx=0\)
\(\Leftrightarrow2sin^2x-5sinx+2+cosx\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sinx-2\right)+cosx\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sinx+cosx-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\\sinx+cosx=2\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Loại nghiệm
\(\Rightarrow x=\dfrac{\pi}{6}+k2\pi\)
\(0\le\dfrac{\pi}{6}+k2\pi\le2022\pi\Rightarrow0\le k\le1010\)
\(\Rightarrow\sum x=1011.\dfrac{\pi}{6}+2\pi\left(0+1+2+...+1010\right)=\dfrac{1011\pi}{6}+2\pi.\dfrac{1010.1011}{2}=...\)
Đúng 2
Bình luận (0)