cho \(f\left[0;1\right]\rightarrow\left[0;1\right]\) thỏa mãn
\(\left\{{}\begin{matrix}f\left(1-x\right)=1-f\left(x\right)\\f\left(\frac{x}{3}\right)=\frac{f\left(x\right)}{2}\end{matrix}\right.\) ∀x∈\(\left[0;1\right]\)
Cho hàm số f(x) thỏa mãn \(\left[f'\left(x\right)\right]^2+f\left(x\right)f''\left(x\right)=15x^4+12x\) ∀x∈R biết
f(0)=f'(0)=1. Tính \(f^2\left(1\right)\)
Vẫn là đạo hàm của tích
Dễ dàng viết được:
\(\left[f'\left(x\right)\right]^2+f\left(x\right).f''\left(x\right)=\left[f\left(x\right)\right]'.f'\left(x\right)+f\left(x\right).\left[f'\left(x\right)\right]'=\left[f'\left(x\right).f\left(x\right)\right]'\)
Do đó giả thiết biến đổi thành:
\(\left[f'\left(x\right).f\left(x\right)\right]'=15x^4+12x\)
Nguyên hàm 2 vế:
\(f'\left(x\right).f\left(x\right)=\int\left(15x^4+12x\right)dx=3x^5+6x^2+C\)
Thay \(x=0\)
\(\Rightarrow f'\left(0\right).f\left(0\right)=C\Rightarrow C=1\)
\(\Rightarrow f'\left(x\right).f\left(x\right)=3x^5+6x^2+1\)
Tiếp tục nguyên hàm 2 vế:
\(\int f\left(x\right).f'\left(x\right)dx=\int\left(3x^5+6x^2+1\right)dx\) với chú ý \(\int f\left(x\right).f'\left(x\right)dx=\int f\left(x\right).d\left[f\left(x\right)\right]=\dfrac{1}{2}f^2\left(x\right)+C\)
Nên:
\(\Rightarrow\dfrac{1}{2}f^2\left(x\right)=\dfrac{1}{2}x^6+2x^3+x+C\)
Thay \(x=0\Rightarrow C=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{1}{2}f^2\left(x\right)=\dfrac{1}{2}x^6+2x^3+x+\dfrac{1}{2}\)
\(\Rightarrow f^2\left(1\right)\)
1, Cho hàm số y=f(x) và f'(0)=3. Hỏi giới hạn \(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x+1}-1}{f\left(0\right)-f\left(x\right)}\)=?
2, Cho hàm số f(x) có đạo hàm trên R và f'(x)=0 có các nghiệm là 1 và -2. Đặt \(g\left(x\right)=f\left(\sqrt{x^2+4}\right)\), hỏi g'(x)=0 có bao nhiêu nghiệm?
Mọi người giúp mình với ạ, mình cần gấp!! Cảm ơn mọi người rất nhiều!!!
1. Áp dụng quy tắc L'Hopital
\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x+1}-1}{f\left(0\right)-f\left(x\right)}=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{1}{2\sqrt{x+1}}}{-f'\left(0\right)}=-\dfrac{1}{6}\)
2.
\(g'\left(x\right)=2x.f'\left(\sqrt{x^2+4}\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\f'\left(\sqrt{x^2+4}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\\sqrt{x^2+4}=1\\\sqrt{x^2+4}=-2\end{matrix}\right.\)
2 pt cuối đều vô nghiệm nên \(g'\left(x\right)=0\) có đúng 1 nghiệm
Cho hàm số \(y = f\left( x \right) = - {x^2} + 1\). Tính \(f\left( { - 3} \right);f\left( { - 2} \right);f\left( { - 1} \right);f\left( 0 \right);f\left( 1 \right)\).
\(f\left( { - 3} \right) = - {\left( { - 3} \right)^2} + 1 = - 9 + 1 = - 8\);
\(f\left( { - 2} \right) = - {\left( { - 2} \right)^2} + 1 = - 4 + 1 = - 3\);
\(f\left( { - 1} \right) = - {\left( { - 1} \right)^2} + 1 = - 1 + 1 = 0\);
\(f\left( 0 \right) = - {0^2} + 1 = 0 + 1 = 1\);
\(f\left( 1 \right) = - {1^2} + 1 = - 1 + 1 = 0\);
Cho hàm số \(y = f\left( x \right) = {x^2} + 4\). Tính \(f\left( { - 3} \right);f\left( { - 2} \right);f\left( { - 1} \right);f\left( 0 \right);f\left( 1 \right)\)
\(f\left( { - 3} \right) = {\left( { - 3} \right)^2} + 4 = 9 + 4 = 13\);
\(f\left( { - 2} \right) = {\left( { - 2} \right)^2} + 4 = 4 + 4 = 8\);
\(f\left( { - 1} \right) = {\left( { - 1} \right)^2} + 4 = 1 + 4 = 5\);
\(f\left( 0 \right) = {0^2} + 4 = 0 + 4 = 4\);
\(f\left( 1 \right) = {1^2} + 4 = 1 + 4 = 5\).
Cho hàm số y = f(x) có đạo hàm cấp hai trên \(\left(0;+\infty\right)\) thỏa mãn: \(2xf'\left(x\right)-f\left(x\right)=x^2\sqrt{x}cosx,\forall x\in\left(0;+\infty\right)\) và \(f\left(4\Pi\right)=0\)
Tính giá trị biểu thức \(f\left(9\Pi\right)\)
\(2x.f'\left(x\right)-f\left(x\right)=x^2\sqrt{x}.cosx\)
\(\Leftrightarrow\dfrac{1}{\sqrt{x}}.f'\left(x\right)-\dfrac{1}{2x\sqrt{x}}f\left(x\right)=x.cosx\)
\(\Leftrightarrow\left[\dfrac{f\left(x\right)}{\sqrt{x}}\right]'=x.cosx\)
Lấy nguyên hàm 2 vế:
\(\int\left[\dfrac{f\left(x\right)}{\sqrt{x}}\right]'dx=\int x.cosxdx\)
\(\Rightarrow\dfrac{f\left(x\right)}{\sqrt{x}}=x.sinx+cosx+C\)
\(\Rightarrow f\left(x\right)=x\sqrt{x}.sinx+\sqrt{x}.cosx+C.\sqrt{x}\)
Thay \(x=4\pi\)
\(\Rightarrow0=4\pi.\sqrt{4\pi}.sin\left(4\pi\right)+\sqrt{4\pi}.cos\left(4\pi\right)+C.\sqrt{4\pi}\)
\(\Rightarrow C=-1\)
\(\Rightarrow f\left(x\right)=x\sqrt{x}.sinx+\sqrt{x}.cosx-\sqrt{x}\)
Cho hàm số \(f\left(x\right)\) có đạo hàm \(f'\left(x\right)\) liên tục trên \(R\) và thỏa mãn các điều kiện \(f\left(x\right)>0,\forall x\in R\), \(f\left(0\right)=1\) và \(f'\left(x\right)=-4x^3.\left(f\left(x\right)\right)^2,\forall x\in R\). Tính \(I=\int_0^1x^3f\left(x\right)dx\)
A.\(I=\dfrac{1}{6}\) B. \(I=ln2\) C. \(I=\dfrac{1}{4}\) D. \(I=\dfrac{ln2}{4}\)
Mình cần bài giải ạ, mình cảm ơn nhiều♥

\(f'\left(x\right)=-4x^3\left(f\left(x\right)\right)^2\Leftrightarrow-\dfrac{f'\left(x\right)}{\left(f\left(x\right)\right)^2}=4x^3\)
Lấy nguyên hàm hai vế
\(\int-\dfrac{f'\left(x\right)}{\left(f\left(x\right)\right)^2}dx=\int4x^3dx\)
\(\Leftrightarrow\dfrac{1}{f\left(x\right)}=x^4+c\)
Thay x=0 vào tìm được c=1 \(\Rightarrow f\left(x\right)=\dfrac{1}{x^4+1}\)
\(I=\int\limits^1_0\dfrac{x^3}{x^4+1}dx=\dfrac{1}{4}\int\limits^1_0\dfrac{\left(x^4+1\right)'}{x^4+1}dx=\dfrac{ln2}{4}\)
Chọn D
Cho hàm số f(x) liên tục trên \(\left(0;+\infty\right)\) thỏa mãn \(f\left(1\right)=\dfrac{1}{3}\) và \(2f\left(x\right)+x^2\dfrac{f'\left(x\right)}{f\left(x\right)}=3x,f\left(x\right)\ne0\) với mọi \(x\in\left(0;+\infty\right)\) . Biết \(\int_1^2f\left(x\right)dx=a+bln\left(2\right)\), \(\left(a,b\in R\right).\) Tính giá trị T=10a+3b
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l} - 1,\,\,x < 0\\0,\,\,x = 0\\1,\,\,x > 0\end{array} \right.\)
Hàm số \(f\left( x \right)\) có đồ thị ở Hình 6.
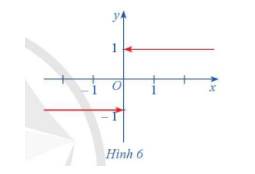
a) Xét dãy số \(\left( {{u_n}} \right)\) sao cho \({u_n} < 0\) và \(\lim {u_n} = 0.\) Xác định \(f\left( {{u_n}} \right)\) và tìm \(\lim f\left( {{u_n}} \right).\)
b) Xét dãy số \(\left( {{v_n}} \right)\) sao cho \({v_n} > 0\) và \(\lim {v_n} = 0.\) Xác định \(f\left( {{v_n}} \right)\) và tìm \(\lim f\left( {{v_n}} \right).\)
a) Xét dãy số \(\left( {{u_n}} \right)\) sao cho \({u_n} < 0\) và \(\lim {u_n} = 0.\) Khi đó \(f\left( {{u_n}} \right) = - 1\) và \(\lim f\left( {{u_n}} \right) = - 1.\)
b) Xét dãy số \(\left( {{v_n}} \right)\) sao cho \({v_n} > 0\) và \(\lim {v_n} = 0.\) Khi đó \(f\left( {{v_n}} \right) = 1\) và \(\lim f\left( {{v_n}} \right) = 1.\)
Cho \(f\left(x\right)=ax^2+bx+c\) (a ,b,c là các số thực )
a) Biết 10a+2b-5c=0 . Chứng minh\(f\left(-1\right).f\left(-4\right)\ge0\)
b) Biết 13a + b + 2c=0 . Chứng minh \(f\left(-2\right).f\left(3\right)\le0\)
Lời giải:
a.
$f(-1)=a-b+c$
$f(-4)=16a-4b+c$
$\Rightarrow f(-4)-6f(-1)=16a-4b+c-6(a-b+c)=10a+2b-5c=0$
$\Rightarrow f(-4)=6f(-1)$
$\Rightarrow f(-1)f(-4)=f(-1).6f(-1)=6[f(-1)]^2\geq 0$ (đpcm)
b.
$f(-2)=4a-2b+c$
$f(3)=9a+3b+c$
$\Rightarrow f(-2)+f(3)=13a+b+2c=0$
$\Rightarrow f(-2)=-f(3)$
$\Rightarrow f(-2)f(3)=-[f(3)]^2\leq 0$ (đpcm)
a.
�
(
−
1
)
=
�
−
�
+
�
f(−1)=a−b+c
�
(
−
4
)
=
16
�
−
4
�
+
�
f(−4)=16a−4b+c
⇒
�
(
−
4
)
−
6
�
(
−
1
)
=
16
�
−
4
�
+
�
−
6
(
�
−
�
+
�
)
=
10
�
+
2
�
−
5
�
=
0
⇒f(−4)−6f(−1)=16a−4b+c−6(a−b+c)=10a+2b−5c=0
⇒
�
(
−
4
)
=
6
�
(
−
1
)
⇒f(−4)=6f(−1)
⇒
�
(
−
1
)
�
(
−
4
)
=
�
(
−
1
)
.
6
�
(
−
1
)
=
6
[
�
(
−
1
)
]
2
≥
0
⇒f(−1)f(−4)=f(−1).6f(−1)=6[f(−1)]
2
≥0 (đpcm)
b.
�
(
−
2
)
=
4
�
−
2
�
+
�
f(−2)=4a−2b+c
�
(
3
)
=
9
�
+
3
�
+
�
f(3)=9a+3b+c
⇒
�
(
−
2
)
+
�
(
3
)
=
13
�
+
�
+
2
�
=
0
⇒f(−2)+f(3)=13a+b+2c=0
⇒
�
(
−
2
)
=
−
�
(
3
)
⇒f(−2)=−f(3)
⇒
�
(
−
2
)
�
(
3
)
=
−
[
�
(
3
)
]
2
≤
0
⇒f(−2)f(3)=−[f(3)]
2
≤0 (đpcm
Cho hàm số y =f(x)=ax+b. Biết \(f\left(3\right)\le f\left(1\right)\le f\left(2\right)\)và f(4)=2. Chứng minh rằng: a=0 và f(0)=2