- Ta có : \(\Delta ABC\) cân tại A .

=> AB = AC ( Tính chất tam giác cân )

=> \(\widehat{ABH}=\widehat{ACH}\) ( Tính chất tam giác cân )

- Xét \(\Delta AHB\) và \(\Delta AHC\) có :

\(\left\{{}\begin{matrix}AB=AC\left(cmt\right)\\\widehat{ABH}=\widehat{ACH}\left(cmt\right)\\AH=AH\end{matrix}\right.\)

=> \(\Delta AHB\) = \(\Delta AHC\) ( c - g -c )

b, Ta có : \(\Delta AHB\) = \(\Delta AHC\) ( câu a )

=> BH = CH ( cạnh tương ứng )

- Xét \(\Delta HMB\) và \(\Delta HNC\) có :

\(\left\{{}\begin{matrix}\widehat{HMB}=\widehat{HNC}\left(=90^o\right)\\BH=CH\left(cmt\right)\\\widehat{ABC}=\widehat{ACB}\left(cmt\right)\end{matrix}\right.\)

=> \(\Delta HMB\) = \(\Delta HNC\) ( Ch - Cgv )

=> MB = NC ( cạnh tương ứng )

Ta có : \(\left\{{}\begin{matrix}AB=AM+BM\\AC=AN+CN\end{matrix}\right.\)

Mà AB = AC (tam giác cân )

=> \(AM=AN\)

- Xét \(\Delta AMN\) có : AM = AN ( cmt )

=> \(\Delta AMN\) là tam giác cân tại A ( đpcm )

c, - Ta có : \(\Delta AMN\) cân tại A ( cmt )

=> \(\widehat{AMN}=\widehat{ANM}\)

Mà \(\widehat{AMN}+\widehat{ANM}+\widehat{MAN}=180^o\)

=> \(\widehat{2AMN}+\widehat{MAN}=180^o\)

=> \(\widehat{AMN}=\frac{180^o-\widehat{MAN}}{2}\) ( I )

- Ta có : \(\Delta ABC\) cân tại A .

=> \(\widehat{ABC}=\widehat{ACB}\)

Mà \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^o\)

=> \(\widehat{2ABC}+\widehat{BAC}=180^o\)

=> \(\widehat{ABC}=\frac{180^o-\widehat{BAC}}{2}\) ( II )

Ta có : \(\widehat{ABC}=\widehat{AMN}\left(=\frac{180^o-\widehat{BAC}}{2}\right)\)

Mà 2 góc trên ở vị trí đồng vị .

=> MN // BC ( Tính chất 2 đoạn thẳng song song )

d, ( Hình vẽ câu trên nha )

- Áp dụng định lý pi - ta - go vào \(\Delta AHB\perp H\) có :

\(AH^2+BH^2=AB^2\)

- Xét \(\Delta AMH\) và \(\Delta AHB\) có :

\(\left\{{}\begin{matrix}\widehat{MAH}=\widehat{BAH}\\\widehat{AMH}=\widehat{AHB}\left(=90^o\right)\end{matrix}\right.\)

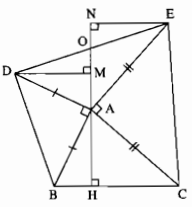
a) Ta có :

=> góc HAB + 90 độ + góc DAM = 180 độ

Xét tam giác AMD :

Từ (1) và (2)

Xét tam giác ADM và tam giác BAH :

AD = AB (gt)

(cmt)

==> ∆ADM = ∆BAH (cạnh huyền - góc nhọn)

=> DM = AH (2 cạnh tương ứng)

b) Ta có:

(kề bù)

=> góc HAC + 90 độ + góc EAN = 180 độ

=> góc EAN = 90 độ - góc HAC (3)

Xét tam giác AHC : góc

góc HCA = 90 độ - góc HAC (4)

Từ (3) và (4) => góc

Xét tam giác AHC và tam giác ENA :

AC = EA (gt)

(cmt)

==> ∆AHC = ∆ENA (cạnh huyền - góc nhọn)

=> AH = EN (2 cạnh tương ứng)

mà DM = AH (chứng minh ở câu a)

==> EN = DM (= AH)

;

=> DM // EN

=> góc MDO = góc NEO (so le trong)

Gọi O là giao điểm MN và DE

Xét tam giác DMO và tam giác ENO :

DM = EN (cmt)

(cmt)

==> ∆DMO = ∆ENO (g.c.g)

=> OD = DE (2 cạnh tương ứng)

Vậy MN đi qua trung điểm của DE

(- Bài này t học rồi, đảm bảo chi tiết và đúng :)) t lấy vở của t ra chép lại cho bn đấy =))

Xét tứ giác AEHF có

góc AEH=góc AFH=góc FAE=90 độ

nên AEHF là hình chữ nhật

=>AH cắt EF tại trung điểm của mỗi đường và AH=EF

=>OE=OF=AH/2

=>OE*OF=1/4*AH^2

=>4*OE*OF=AH^2=HB*HC

a) Xét ΔABH vuông tại H và ΔACH vuông tại H có

AB=AC(ΔABC cân tại A)

AH là cạnh chung

Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)

b) Ta có: ΔABH=ΔACH(cmt)

⇒\(\widehat{BAH}=\widehat{CAH}\)(hai góc tương ứng)

hay \(\widehat{MAH}=\widehat{NAH}\)

Xét ΔAMH vuông tại M và ΔANH vuông tại N có

AH là cạnh chung

\(\widehat{MAH}=\widehat{NAH}\)(cmt)

Do đó: ΔAMH=ΔANH(cạnh huyền-góc nhọn)

⇒AM=AN(hai cạnh tương ứng)

c) Ta có: ΔAHB=ΔAHC(cmt)

⇒HB=HC(hai cạnh tương ứng)

Xét ΔBMH và ΔCNH có

HB=HC(cmt)

\(\widehat{B}=\widehat{C}\)(hai góc ở đáy trong ΔABC cân tại A)

Do đó: ΔBMH=ΔCNH(cạnh huyền-góc nhọn)

d) Xét ΔAMN có AM=AN(cmt)

nên ΔAMN cân tại A(định nghĩa tam giác cân)

⇒\(\widehat{AMN}=\frac{180^0-\widehat{A}}{2}\)(số đo của một góc ở đáy trong ΔAMN cân tại A)(1)

Ta có: ΔABC cân tại A(gt)

⇒\(\widehat{ABC}=\frac{180^0-\widehat{A}}{2}\)(số đo của một góc ở đáy trong ΔABC cân tại A)(2)

Từ (1) và (2) suy ra \(\widehat{AMN}=\widehat{ABC}\)

mà \(\widehat{AMN}\) và \(\widehat{ABC}\) là hai góc ở vị trí đồng vị

nên MN//BC(dấu hiệu nhận biết hai đường thẳng song song)

e)

*Tính AB

Ta có: HB=HC(cmt)

mà HB+HC=BC(H nằm giữa B và C)

nên \(BH=CH=\frac{BC}{2}=\frac{12cm}{2}=6cm\)

Áp dụng định lí pytago vào ΔABH vuông tại H, ta được

\(AB^2=BH^2+AH^2\)

hay \(AB^2=6^2+8^2=100\)

⇒\(AB=\sqrt{100}=10cm\)

Vậy: AB=10cm

a) Xét △ABC,ta có :△ABC cân tại A nên

AB=AC, ∠ABC = ∠ACB( t/c tam giác cân)

Vì AH⊥BC nên ∠AHB = ∠AHC

# Xét △AHB vs △AHC, ta có :

∠AHB=∠AHC(=90^o)

AB=AC

∠ABC = ∠ACB

⇒△AHB = △AHC(ch-gn)

⇒HB=HC( 2 cạnh tương ứng )

b)Vì △AHB = △AHC(cmt) nên ∠HAB = ∠HAC(2 góc tương ứng)

Vì HM ⊥ AB nên ∠HMA =90^o

Vì HN ⊥ AC nên ∠HMB =90^o

#Xét △AHM vs △AHN, ta có:

∠AHM =∠AHN(=90^o)

AH là cạnh chung

∠MAH=∠NAH(cmt)

⇒△AHM = △AHN (ch-gn)

c) Lúc nữa.

Ý cuối nhầm không thế ạ?

a) Xét ΔAHB vuông tại H và ΔADH vuông tại D có 

\(\widehat{DAH}\) chung

Do đó: ΔAHB\(\sim\)ΔADH(g-g)

a) Xét ΔAHC vuông tại H và ΔAEH vuông tại E có 

\(\widehat{HAE}\) chung

Do đó: ΔAHC\(\sim\)ΔAEH(g-g)

a.Theo định lí Py-ta-go, ta có:

BC²=AB²+AC²

⇒BC²= 6²+8²

⇒BC²= 36+64

⇒BC²= 100

⇒BC= 10

Vậy BC= 10cm

a: \(AC=\sqrt{8^2-6^2}=\sqrt{64-36}=2\sqrt{7}\left(cm\right)\)

b: \(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{6\cdot2\sqrt{7}}{8}=\dfrac{3}{2}\sqrt{7}\left(cm\right)\)