Mình cần gấp câu này ạaaaaaa !!!!!!!!!!!!!
 gấp ạaaaaaa
gấp ạaaaaaa
bạn ơi, đề hình như bị thiếu đáp án, mà đáp án bị thiếu có khi là đáp án đúng á, chứ đây sai hết
giải hệ bất phương trình. em cần gấp lắm ạaaaaaa
\(\left\{{}\begin{matrix}3x^2+5x-2\text{≥}0\\-x^2+x+12\text{≥}0\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}\left(3x-1\right)\left(x+2\right)\ge0\\\left(4-x\right)\left(x+3\right)\ge0\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}x\ge\dfrac{1}{3},x\le-2\\-3\le x\le4\end{matrix}\right.\)
\(< =>\dfrac{1}{3}\le x\le4,-3\le x\le-2\)
giúp mình câu này nha khẩn cấp mình cần gấp gấp lắm rồi
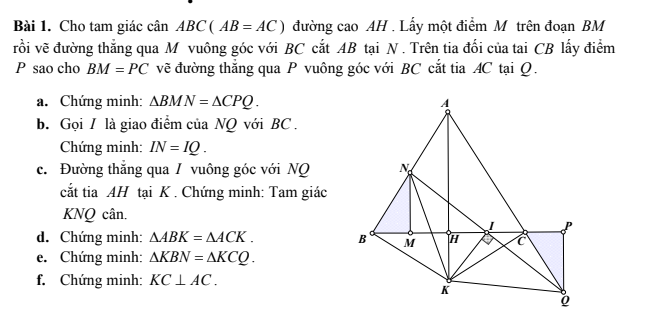
a, Vì tam giác ABC cân tại A nên \(\widehat{NBM}=\widehat{ACB}\)
Mà \(\widehat{ACB}=\widehat{PCQ}\left(đối.đỉnh\right)\Rightarrow\widehat{NBM}=\widehat{PCQ}\)
Mà \(\widehat{NMB}=\widehat{CPQ}=90^0;BM=PC\)
Do đó \(\Delta BMN=\Delta CPQ\left(g.c.g\right)\)
b, Vì \(BM//PQ\left(\perp BP\right)\) nên \(\widehat{MNI}=\widehat{IQP}\)
Mà \(\widehat{NMI}=\widehat{IPQ}=90^0;MN=PQ\left(\Delta BMN=\Delta CPQ\right)\)
Do đó \(\Delta IMN=\Delta IPQ\left(g.c.g\right)\)
\(\Rightarrow IN=IQ\)
c, Vì IK là đường cao cũng là trung tuyến tam giác KNQ nên tam giác KNQ cân tại K
Giúp mình câu này với mình cần gấp
uses crt;
var st:string;
d,i:integer;
begin
clrscr;
readln(st);
d:=length(st);
for i:=1 to d do
if (st[i] in ['0'..'9']) then write(st[i]);
readln;
end.
Giúp mình câu này, mình đang cần gấp 
24:
góc HKI<góc BAC<góc PQT<góc DEG
25:
A=1/3(3/4*7+3/7*10+...+3/100*103)
=1/3(1/4-1/7+1/7-1/10+...+1/100-1/103)
=1/3*99/412
=33/412
Giúp mình câu này đi mình cần gấp 
Bài 6:
-Thay \(x=1\) vào \(f\left(x\right)=x\left(x+1\right)+\left(x+1\right)\left(x+2\right)+...+\left(x+49\right)\left(x+50\right)\), ta được:
\(f\left(1\right)=1\left(1+1\right)+\left(1+1\right)\left(1+2\right)+...+\left(1+49\right)\left(1+50\right)\)
\(=1.2+2.3+...+50.51\)
\(=\dfrac{1.2.3+2.3.3+...+50.51.3}{3}\)
\(=\dfrac{1.2.3+2.3.\left(4-1\right)+...+50.51.\left(52-49\right)}{3}\)
\(=\dfrac{1.2.3+2.3.4-1.2.3+...+50.51.52-49.50.51}{3}\)
\(=\dfrac{50.51.52}{3}=44200\)
Giúp mình câu này với mình đang cần gấp

Phương trình tương đương
\(\left[{}\begin{matrix}x=\dfrac{5\pi}{12}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\end{matrix}\right.,k\in Z\)
Xét họ nghiệm \(x=\dfrac{5\pi}{12}+k\pi,k\in Z\).
Do \(-\dfrac{\pi}{2}< \dfrac{5\pi}{12}+k\pi< \dfrac{8\pi}{3}\) nên \(-\dfrac{11\pi}{12}< k\pi< \dfrac{9\pi}{4}\)
⇒ \(-\dfrac{11}{12}< k< \dfrac{9}{4}\). Mà k ∈ Z nên k ∈ {0 ; 1}
Vậy các nghiệm thỏa mãn phương trình là các phần tử của tập hợp :
S1 = \(\left\{\dfrac{5\pi}{12};\dfrac{17\pi}{12}\right\}\)
Xét họ nghiệm \(x=-\dfrac{\pi}{4}+k\pi\) với k ∈ Z.
Do \(-\dfrac{\pi}{2}< \dfrac{-\pi}{4}+k\pi< \dfrac{8\pi}{3}\) nên \(-\dfrac{\pi}{4}< k\pi< \dfrac{35\pi}{12}\)
nên \(-\dfrac{1}{4}< k< \dfrac{35}{12}\). Mà k ∈ Z nên k∈ {0 ; 1 ; 2}
Vậy các nghiệm thỏa mãn phương trình là các phần tử của tập hợp
S2 = \(\left\{-\dfrac{\pi}{4};\dfrac{3\pi}{4};\dfrac{7\pi}{4}\right\}\)
Vậy các nghiệm thỏa mãn phương trình là các phần tử của tập hợp
S = S1 \(\cup\) S2 = \(\left\{\dfrac{5\pi}{12};\dfrac{17\pi}{12};-\dfrac{\pi}{4};\dfrac{3\pi}{4};\dfrac{7\pi}{4}\right\}\)
Giúp mình câu này với mình đang cần gấp
a: \(\widehat{\left(SC;\left(ABCD\right)\right)}=\widehat{CS;CA}=\widehat{SCA}\)
Ta có: SA\(\perp\)(ABCD)
=>SA\(\perp\)AC
=>ΔSAC vuông tại A
Vì ABCD là hình vuông
nên \(AC=AD\cdot\sqrt{2}=a\sqrt{2}\)
Xét ΔSAC vuông tại A có \(tanSCA=\dfrac{SA}{AC}=\dfrac{a\sqrt{6}}{a\sqrt{2}}=\sqrt{3}\)
nên \(\widehat{SCA}=60^0\)
=>\(\widehat{SC;\left(ABCD\right)}=60^0\)
b: Ta có: BD\(\perp\)AC
BD\(\perp\)SA
SA,AC cùng thuộc mp(SAC)
Do đó: BD\(\perp\)(SAC)
\(\widehat{SB;\left(SAC\right)}=\widehat{SB;SD}=\widehat{BSD}\)
Vì ABCD là hình vuông
nên \(AC=BD=a\sqrt{2}\)
ΔSAD vuông tại A
=>\(SA^2+AD^2=SD^2\)
=>\(SD^2=\left(a\sqrt{6}\right)^2+a^2=7a^2\)
=>\(SD=a\sqrt{7}\)
ΔSAB vuông tại A
=>\(SA^2+AB^2=SB^2\)
=>\(SB=a\sqrt{7}\)
Xét ΔSBD có \(cosBSD=\dfrac{SB^2+SD^2-BD^2}{2\cdot SB\cdot SD}\)
\(=\dfrac{7a^2+7a^2-2a^2}{2\cdot a\sqrt{7}\cdot a\sqrt{7}}=\dfrac{6}{7}\)
=>\(sinBSD=\sqrt{1-\left(\dfrac{6}{7}\right)^2}=\dfrac{\sqrt{13}}{7}\)
=>\(\widehat{BSD}\simeq31^0\)
=>\(\widehat{SB;\left(SAC\right)}\simeq31^0\)
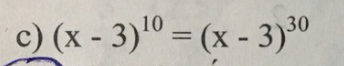 giúp mình câu này với mình đang cần gấp
giúp mình câu này với mình đang cần gấp
\(\left(x-3\right)^{30}=\left(x-3\right)^{10}\)
\(\Leftrightarrow\left(x-3\right)\left(x-2\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\\x=4\end{matrix}\right.\)
Giúp mình câu này với mình đang cần gấp
different
composed
knowledge
width
widen
funny
hungry
fame
Different,composed,knowledge,width,widen,funny,hungry,fame