Bài 6:
-Thay \(x=1\) vào \(f\left(x\right)=x\left(x+1\right)+\left(x+1\right)\left(x+2\right)+...+\left(x+49\right)\left(x+50\right)\), ta được:
\(f\left(1\right)=1\left(1+1\right)+\left(1+1\right)\left(1+2\right)+...+\left(1+49\right)\left(1+50\right)\)
\(=1.2+2.3+...+50.51\)
\(=\dfrac{1.2.3+2.3.3+...+50.51.3}{3}\)
\(=\dfrac{1.2.3+2.3.\left(4-1\right)+...+50.51.\left(52-49\right)}{3}\)
\(=\dfrac{1.2.3+2.3.4-1.2.3+...+50.51.52-49.50.51}{3}\)
\(=\dfrac{50.51.52}{3}=44200\)








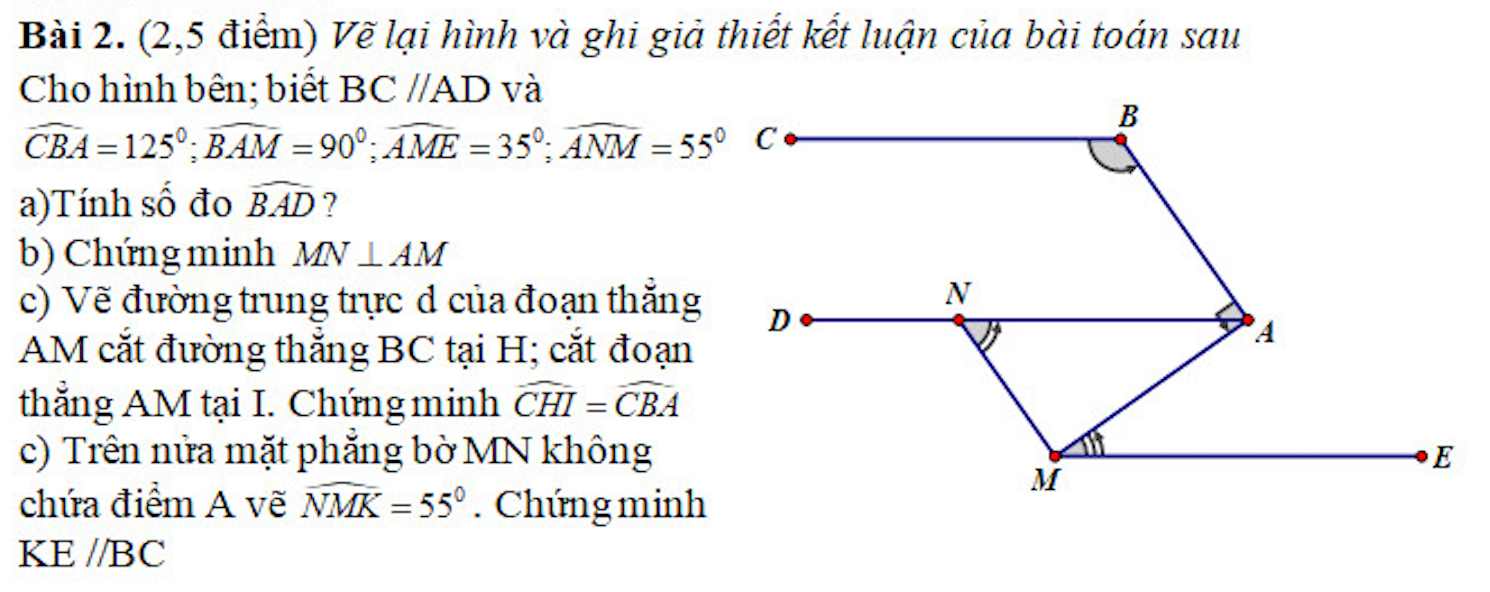
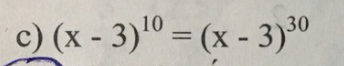 giúp mình câu này với mình đang cần gấp
giúp mình câu này với mình đang cần gấp
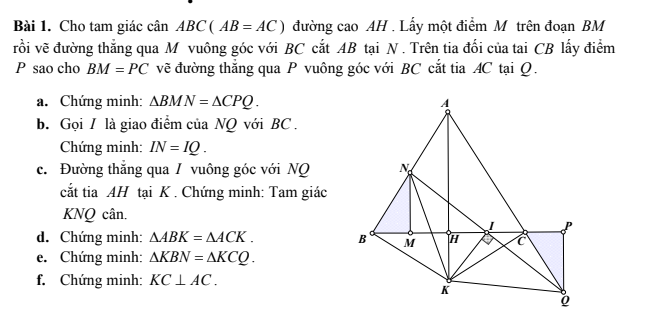
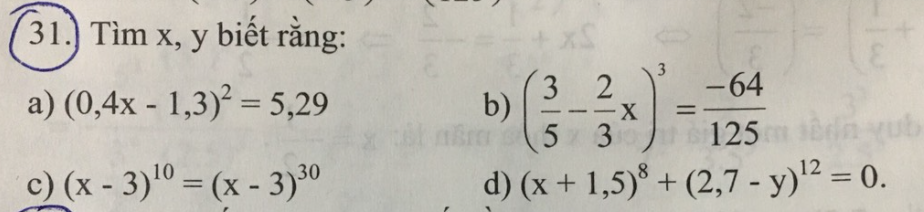 giúp mình 4 câu này với mình đang cần gấp
giúp mình 4 câu này với mình đang cần gấp 


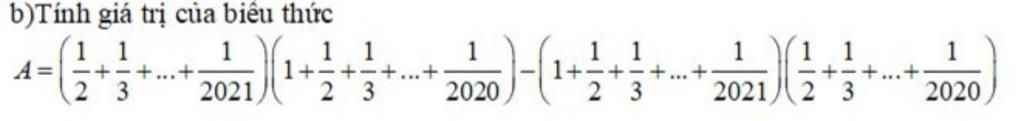
 giúp mình 2 câu này với ạ mình đang cần gấp
giúp mình 2 câu này với ạ mình đang cần gấp