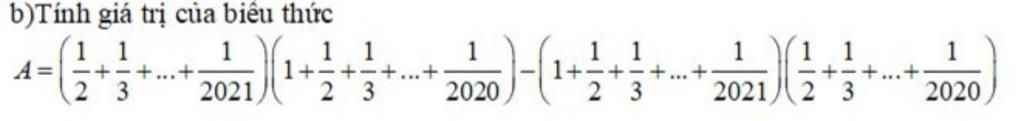a) Do \(\left(3x-\dfrac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow A=\left(3x-\dfrac{1}{2}\right)^2-4\ge-4\)
\(minA=-4\Leftrightarrow x=\dfrac{1}{6}\)
b) Do \(\left(2x+1\right)^4\ge0\forall x,\left(y-\dfrac{1}{2}\right)^6\ge0\forall y\)
\(\Rightarrow B=\left(2x+1\right)^4+3\left(y-\dfrac{1}{2}\right)^6\ge0\)
\(minB=0\Leftrightarrow\)\(\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=\dfrac{1}{2}\end{matrix}\right.\)
a: \(A=\left(3x-\dfrac{1}{2}\right)^2-4\ge-4\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{6}\)
b: \(B=\left(2x+1\right)^4+3\left(y-\dfrac{1}{2}\right)^6\ge0\forall x,y\)
Dấu '=' xảy ra khi \(\left(x,y\right)=\left(-\dfrac{1}{2};\dfrac{1}{2}\right)\)

 giúp mình 2 câu này với ạ mình đang cần gấp
giúp mình 2 câu này với ạ mình đang cần gấp




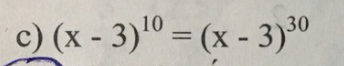 giúp mình câu này với mình đang cần gấp
giúp mình câu này với mình đang cần gấp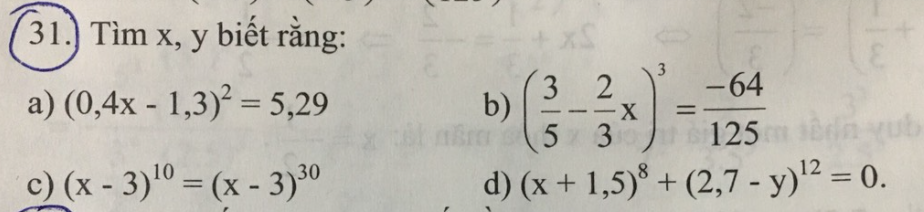 giúp mình 4 câu này với mình đang cần gấp
giúp mình 4 câu này với mình đang cần gấp