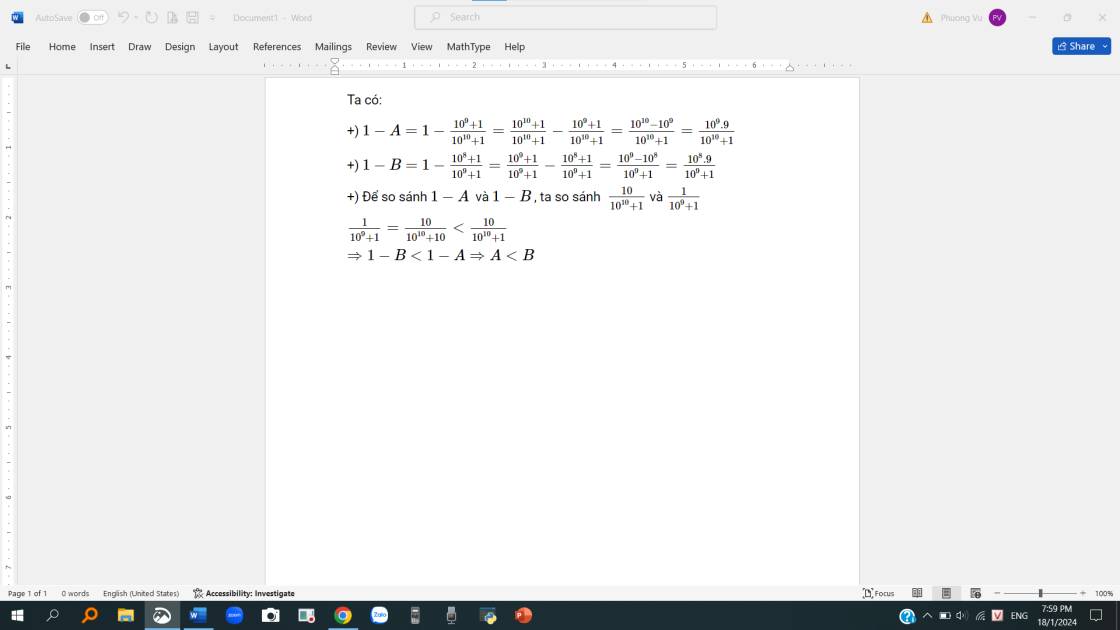
So sánh hai ps A=\(\dfrac{10^8+1}{10^9+1}\) và B=\(\dfrac{10^9+1}{10^{10}+1}\)
Những câu hỏi liên quan
So sánh
A = \(\dfrac{3^{10}+1}{3^9+1}\) và B = \(\dfrac{3^9+1}{3^8+1}\)
Ta có: \(A=\dfrac{3^{10}+1}{3^9+1}\)
\(\Leftrightarrow A=\dfrac{3^{10}+3-2}{3^9+1}\)
hay \(A=3-\dfrac{2}{3^9+1}\)
Ta có: \(B=\dfrac{3^9+1}{3^8+1}\)
\(\Leftrightarrow B=\dfrac{3^9+3-2}{3^8+1}\)
hay \(B=3-\dfrac{2}{3^8+1}\)
Ta có: \(3^9+1>3^8+1\)
\(\Leftrightarrow\dfrac{2}{3^9+1}< \dfrac{2}{3^8+1}\)
\(\Leftrightarrow-\dfrac{2}{3^9+1}>-\dfrac{2}{3^8+1}\)
\(\Leftrightarrow-\dfrac{2}{3^9+1}+3>-\dfrac{2}{3^8+1}+3\)
hay A>B
Đúng 1
Bình luận (0)
SGK Cánh diều - Tập 2 - Trang 23
10 tháng 10 2023 lúc 21:45
So sánh hai phân số:a) dfrac{1}{5} và dfrac{3}{5} b) dfrac{9}{10} và dfrac{3}{10} c) dfrac{7}{12} và dfrac{11}{12} d) dfrac{7}{8} và dfrac{5}{8}e) dfrac{17}{100} và dfrac{23}{100} g) dfrac{4}{10} và dfrac{1}{10} h) dfrac{100}{100} và dfrac{49}{100} k) dfrac{15}{15} và dfrac{2}{15}
Đọc tiếp
So sánh hai phân số:
a) \(\dfrac{1}{5}\) và \(\dfrac{3}{5}\) b) \(\dfrac{9}{10}\) và \(\dfrac{3}{10}\) c) \(\dfrac{7}{12}\) và \(\dfrac{11}{12}\) d) \(\dfrac{7}{8}\) và \(\dfrac{5}{8}\)
e) \(\dfrac{17}{100}\) và \(\dfrac{23}{100}\) g) \(\dfrac{4}{10}\) và \(\dfrac{1}{10}\) h) \(\dfrac{100}{100}\) và \(\dfrac{49}{100}\) k) \(\dfrac{15}{15}\) và \(\dfrac{2}{15}\)
a) \(< \)
b) \(>\)
c) \(< \)
d) \(>\)
e) \(< \)
g) \(>\)
h) \(>\)
k) \(>\)
Đúng 1
Bình luận (0)
So sánh hai phân số sau : A=\(\dfrac{10^9+1}{10^{10}+1}\);B=\(\dfrac{10^8+1}{10^9+1}\)
\(A=\dfrac{10^9+1}{10^{10}+1}>B=\dfrac{10^8+1}{10^9+1}\)
Đúng 1
Bình luận (0)
Cho A = \(\dfrac{n^9+1}{n^{10}+1}\) và B = \(\dfrac{n^8+1}{n^9+1}\) trong đó n\(\in\)N; n>1. Hãy so sánh nghịch đảo của A và B rồi so sánh A với B
A = \(\dfrac{n^9+1}{n^{10}+1}\)
\(\dfrac{1}{A}\) = \(\dfrac{n^{10}+1}{n^9+1}\) = n - \(\dfrac{n-1}{n^9+1}\)
B = \(\dfrac{n^8+1}{n^9+1}\)
\(\dfrac{1}{B}\) = \(\dfrac{n^9+1}{n^8+1}\) = n - \(\dfrac{n-1}{n^8+1}\)
Vì n > 1 ⇒ n - 1> 0
\(\dfrac{n-1}{n^9+1}\) < \(\dfrac{n-1}{n^8+1}\)
⇒ n - \(\dfrac{n-1}{n^9+1}\) > n - \(\dfrac{n-1}{n^8+1}\)⇒ \(\dfrac{1}{A}>\dfrac{1}{B}\)
⇒ A < B
Đúng 0
Bình luận (0)
So sánh: A = \(\dfrac{2021^{10}-1}{2021^9-1}\)và B = \(\dfrac{2021^{11}-1}{2021^{10}-1}\) làm ơn hãy giúp tôii đi màaaa
\(A=\dfrac{2021^{10}-2021+2020}{2021^9-1}\\ =\dfrac{2021\left(2021^9-1\right)+2020}{2021^9-1}\\ =2021+\dfrac{2020}{2021^9-1}\\ B=\dfrac{2021^{11}-1}{2021^{10}-1}=2021+\dfrac{2020}{2021^{10}-1}\)
Ta có:
\(2021^9-1< 2021^{10}-1\\ \Rightarrow\dfrac{2020}{2021^9-1}>\dfrac{2020}{2021^{10}-1}\)
Do đó A > B.
Đúng 1
Bình luận (0)
Không quy đồng ,hãy so sánh hai phân số
a \(\dfrac{19}{10}và\dfrac{10}{11}\)
b \(\dfrac{11}{10}và\dfrac{12}{11}\)
c \(\dfrac{9}{10}và\dfrac{10}{11}\)
a. 19/10 > 10/11
b. 11/10 = 12/11
c. 9/10 = 10/11
Đúng 0
Bình luận (0)
a)\(\dfrac{19}{10}>\dfrac{10}{11}\)
b)\(\dfrac{11}{10}=\dfrac{12}{11}\)
c)\(\dfrac{9}{10}< \dfrac{10}{11}\)
Đúng 0
Bình luận (0)
a, Cho a,b,n ϵ N* . Hãy so sánh dfrac{a+n}{b+n}vàdfrac{a}{b}b, Cho A dfrac{10^{11}-1}{10^{12}-1};Bdfrac{10^{10}+1}{10^{11}+1}. So sánh A và B
Đọc tiếp
a, Cho a,b,n ϵ N* . Hãy so sánh \(\dfrac{a+n}{b+n}và\dfrac{a}{b}\)
b, Cho A= \(\dfrac{10^{11}-1}{10^{12}-1};B=\dfrac{10^{10}+1}{10^{11}+1}.\) So sánh A và B
Lời giải:
a) Xét hiệu \(\frac{a+n}{b+n}-\frac{a}{b}=\frac{(a+n).b-a(b+n)}{b(b+n)}=\frac{n(b-a)}{b(b+n)}\)
Nếu $b>a$ thì $\frac{a+n}{b+n}-\frac{a}{b}>0\Rightarrow \frac{a+n}{b+n}>\frac{a}{b}$
Nếu $b<a$ thì $\frac{a+n}{b+n}-\frac{a}{b}<0\Rightarrow \frac{a+n}{b+n}<\frac{a}{b}$
Nếu $b=a$ thì $\frac{a+n}{b+n}-\frac{a}{b}=0\Rightarrow \frac{a+n}{b+n}=\frac{a}{b}$
b) Rõ ràng $10^{11}-1< 10^{12}-1$.
Đặt $10^{11}-1=a; 10^{12}-1=b; 11=n$ thì: $a< b$; $A=\frac{a}{b}$ và $B=\frac{10^{11}+10}{10^{12}+10}=\frac{a+n}{b+n}$
Áp dụng kết quả phần a:
$b>a\Rightarrow \frac{a+n}{b+n}>\frac{a}{b}$ hay $B>A$
Đúng 2
Bình luận (2)
Bài 2: So sánh các phân số sau mà không quy đồng mẫu số và tử số:
a)\(\dfrac{2025}{2022}\)và\(\dfrac{2024}{2021}\)
b)\(\dfrac{8^9+1}{8^{10}+1}\)và \(\dfrac{8^8+1}{8^9+1}\)
giúp mk với nhé
So sánh 2 phân số
A=\(\dfrac{10^8+1}{10^9+1}\) và B=\(\dfrac{10^9+1}{10^{10}+1}\)
\(\dfrac{a}{b}< 1\Leftrightarrow\dfrac{a}{b}< \dfrac{a+m}{b+m}\)\(\left(a,b,m\in N\cdot\right)\)
Ta có:
\(B=\dfrac{10^9+1}{10^{10}+1}< 10\left(10^9< 10^{10}\right)\)
\(\Leftrightarrow B=\dfrac{10^9+1}{10^{10}+1}< \dfrac{10^9+1+9}{10^{10}+1+9}=\dfrac{10^9+10}{10^{10}+10}=\dfrac{10\left(10^8+1\right)}{10\left(10^9+1\right)}=\dfrac{10^8+1}{10^9+1}=A\)
\(\Leftrightarrow A>B\)
Đúng 0
Bình luận (0)
1 tháng 4 2021 lúc 20:16
so sánh
a)\(A=\dfrac{-2015}{2015.2016}\) và \(B=\dfrac{-2014}{2014.2015}\) b)A = \(\dfrac{10^{2009}+1}{10^{2010}+1}\) và \(B=\dfrac{10^{2010}+1}{10^{2011}+1}\)
A=-2015/2015x2016
A=-1/2016
B=-2014/2014x2015
B=-1/2015
vi 2016>2015,-1/2016>-1/2015
vay A>B
Đúng 0
Bình luận (0)
b) Ta có: \(A=\dfrac{10^{2009}+1}{10^{2010}+1}\)
\(\Leftrightarrow10A=\dfrac{10^{2010}+10}{10^{2010}+1}=1+\dfrac{9}{10^{2010}+1}\)
Ta có: \(B=\dfrac{10^{2010}+1}{10^{2011}+1}\)
\(\Leftrightarrow10B=\dfrac{10^{2011}+10}{10^{2011}+1}=1+\dfrac{9}{10^{2011}+1}\)
Ta có: \(10^{2010}+1< 10^{2011}+1\)
\(\Leftrightarrow\dfrac{9}{10^{2010}+1}>\dfrac{9}{10^{2011}+1}\)
\(\Leftrightarrow\dfrac{9}{10^{2010}+1}+1>\dfrac{9}{10^{2011}+1}+1\)
\(\Leftrightarrow10A>10B\)
hay A>B
Đúng 0
Bình luận (0)