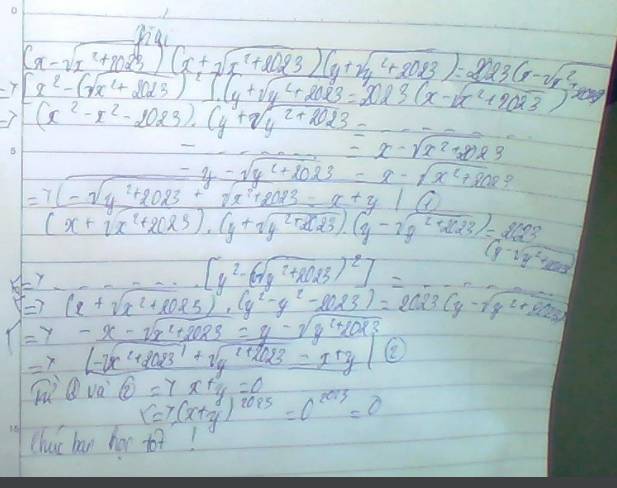\(\sqrt{x}\)I y\(^2\)+1 I -2023

Những câu hỏi liên quan
\(A=\sqrt{-1}+\sqrt{-2}+\sqrt{-3}+...+\sqrt{-2023}\)
gợi ý:
\(\sqrt{-1}=i\) ; \(\sqrt{-2}=2.i\)
vậy:
A= i+2.i+3.i+4.i+...+2023.i
A=N.i
A = i + 2i + 3i + ... + 2023i
= (2023.2024:2)i
= 2047276i
Đúng 1
Bình luận (0)
Cho \(\left(x+\sqrt{x^2+2023}\right)\left(y+\sqrt{y^2+2023}\right)=2023
\)
Tính (x+y)2023
Helpppppppppp
Để tính (x+y)2023, ta sẽ sử dụng công thức nhân đa thức. Trước tiên, ta mở đuôi công thức:(x+y)2023 = (x+y)(x+y)(x+y)...(x+y)Từ phép nhân đầu tiên, ta có:(x+y)(x+y) = x^2 + 2xy + y^2Tiếp tục nhân với (x+y), ta có:(x^2 + 2xy + y^2)(x+y) = x^3 + 3x^2y + 3xy^2 + y^3Lặp lại quá trình này 2020 lần nữa, ta có:(x^3 + 3x^2y + 3xy^2 + y^3)(x+y) = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4Tiếp tục nhân với (x+y), ta có:(x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4)(x+y) = x^5 + 5x^4y + 10x^3
Đúng 0
Bình luận (2)
Để tính (x+y)2023, ta sẽ sử dụng công thức nhân đa thức.
Trước tiên, ta mở đuôi công thức:
(x+y)2023 = (x+y)(x+y)(x+y)...(x+y)
Từ phép nhân đầu tiên, ta có:
(x+y)(x+y) = x^2 + 2xy + y^2
Tiếp tục nhân với (x+y), ta có:
(x^2 + 2xy + y^2)(x+y) = x^3 + 3x^2y + 3xy^2 + y^3
Lặp lại quá trình này 2020 lần nữa, ta có:
(x^3 + 3x^2y + 3xy^2 + y^3)(x+y) = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4
Tiếp tục nhân với (x+y), ta có:
(x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4)(x+y) = x^5 + 5x^4y + 10x^3
Đúng 0
Bình luận (0)
Cho \(\left(x+\sqrt{x^2+2023}\right)\left(y+\sqrt{y^2+2023}\right)=2023\)
Tính (x+y)2023
Help me plsss
Bài 4. (1,0 điểm)
Giải phương trình $\sqrt{x+3} . x^4=2 x^4-2023 x+2023$.
Bài 4: \(\sqrt{x+3}\cdot x^4=2x^4-2023x+2023\) (ĐK: x ≥ -3)
⇔ \(x^4\left(\sqrt{x+3}-2\right)+2023\left(x-1\right)=0\)
⇔ \(x^4\left(\dfrac{x-1}{\sqrt{x+3}+2}\right)+2023\left(x-1\right)=0\)
⇔ \(\left(x-1\right)\left(\dfrac{x^4}{\sqrt{x+3}+2}+2023\right)=0\)
⇒ \(x-1=0\)
⇔ \(x=1\left(TM\right)\)
Vậy S ∈ {1}
Đúng 0
Bình luận (0)
1) Cho các số thực dương x,y,z thỏa mãn điều kiện x\(\sqrt{2020-y^2}\) + y\(\sqrt{2020-z^2}\) +z\(\sqrt{2023-x^2}\)=3030. Tính giá trị vủa biểu thức A=x\(^2\)+\(y^2\)+\(z^2\)
Lời giải:
Áp dụng BĐT AM-GM:
\(x\sqrt{2020-y^2}+y\sqrt{2020-z^2}+z\sqrt{2020-x^2}\leq \frac{x^2+(2020-y^2)}{2}+\frac{y^2+(2020-z^2)}{2}+\frac{z^2+(2020-x^2)}{2}=3030\)Dấu "=" xảy ra khi:
\(\left\{\begin{matrix} x^2=2020-y^2\\ y^2=2020-z^2\\ z^2=2020-x^2\end{matrix}\right.\Rightarrow x=y=z=\sqrt{1010}\)
Khi đó:
$A=3(\sqrt{1010})^2=3030$
Đúng 0
Bình luận (0)
Bài 3 (1,5 điểm). Cho hàm số y = x ^ 2 có đồ thị (P). a) Vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy. X b) Tìm tất cả các giá trị của tham số m để tại hai điểm phân biệt sqrt(x_{1} + 2023) - x_{1} = sqrt(x_{2} + 2023) - x_{2} có để đường thẳng (d): y = (m - 2) * x + 3 cắt (P) hoành độ là X1, x thoả mãn sqrt(x_{1} + 2023) - x_{1} = sqrt(x_{2} + 2023) - x_{2}
Câu 1: Cho bt: A left(dfrac{1}{sqrt{1+x}}+sqrt{1-x}right):left(dfrac{1}{sqrt{1-x^2}}+1right)
a) Tìm x để A có nghĩa
b) Rút gọn
c) Tính A với x dfrac{sqrt{3}}{2+sqrt{3}}
Câu 2: Cho bt B left(dfrac{x-y}{sqrt{x}-sqrt{y}}+dfrac{xsqrt{x}-ysqrt{y}}{y-x}right):left(dfrac{left(sqrt{x}-sqrt{y}right)^2+sqrt{xy}}{sqrt{x}+sqrt{y}}right)
a) Rút gọn
b) CM Bge0
c) So sánh B với sqrt{B}
Đọc tiếp
Câu 1: Cho bt: A= \(\left(\dfrac{1}{\sqrt{1+x}}+\sqrt{1-x}\right):\left(\dfrac{1}{\sqrt{1-x^2}}+1\right)\)
a) Tìm x để A có nghĩa
b) Rút gọn
c) Tính A với x =\(\dfrac{\sqrt{3}}{2+\sqrt{3}}\)
Câu 2: Cho bt B= \(\left(\dfrac{x-y}{\sqrt{x}-\sqrt{y}}+\dfrac{x\sqrt{x}-y\sqrt{y}}{y-x}\right):\left(\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2+\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\right)\)
a) Rút gọn
b) CM B\(\ge\)0
c) So sánh B với \(\sqrt{B}\)
cho \(\sqrt{x+2022}+x^3=\sqrt{y+2022}+y^3\). Tìm max P=\(2x^2-5y^2+xy+12x+2023\)
\(\Leftrightarrow\left(\sqrt{x+2022}-\sqrt{y+2022}\right)+\left(x^3-y^3\right)=0\)
=>\(\dfrac{x-y}{\sqrt{x+2022}+\sqrt{y+2022}}+\left(x-y\right)\left(x^2+xy+y^2\right)=0\)
=>x-y=0
=>x=y
P=2x^2-5x^2+x^2+12x+2023
=-2x^2+12x+2023
=-2(x^2-6x-2023/2)
=-2(x^2-6x+9-2041/2)
=-2(x-3)^2+2041<=2041
Dấu = xảy ra khi x=3
Đúng 1
Bình luận (0)
( x + 3 )2022 + ( \(\sqrt{y-2}\) - 1 )2023 = 0
mình cần gấp mong mọi người giúp ạ!!
\(\left(x+3\right)^{2022}+\left(\sqrt{y-2}-1\right)^{2023}=0\) \(\left(ĐKXĐ: y\ge2\right)\)
Xét \(\left(x+3\right)^{2022}\ge0\forall x\)
\(\Rightarrow\left(\sqrt{y-2}-1\right)^{2023}\le0\)
\(\Leftrightarrow\sqrt{y-2}-1\le0\)
\(\Leftrightarrow\sqrt{y-2}\le1\)
\(\Leftrightarrow y-2\le1\)
\(\Rightarrow y\le3\)
\(\Rightarrow2\le y\le3\) mà \(y\in Z\)
\(\Rightarrow\left\{{}\begin{matrix}y=2\Leftrightarrow x=-2\\y=3\Leftrightarrow x=-3\end{matrix}\right.\)
Đúng 2
Bình luận (1)
Tìm giá trị nhỏ nhất cảu biểu thức : \(x^2+2xy+2y^2+2\sqrt{2}x+2\left(\sqrt{2}+1\right)y+2023\)