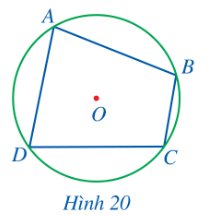
Quan sát Hình 20 và cho biết các đỉnh của tứ giác ABCD có thuộc đường tròn (O) hay không?
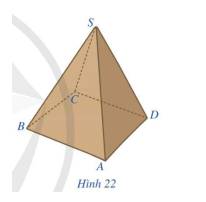
Hình 22 là hình ảnh của một hộp quà lưu niệm có dạng hình chóp tứ giác đều S.ABCD. Quan sát Hình 22 và trả lời các câu hỏi:
a) Đỉnh S có nằm trong mặt phẳng (ABCD) hay không?
b) Mỗi mặt của hộp quà lưu niệm có dạng hình gì?
a) Đỉnh S không nằm trong mặt phẳng (ABCD).
b) Một mặt của hộp quà lưu niệm có dạng hình tam giác.
Cho hình vuông ABCD có cạnh bằng a , biết hai đường chéo cắt nhau tại O . Lấy điểm I thuộc cạnh AB , điểm M thuộc cạnh BC sao ch\(\widehat{IOM}=90^o\)(I và M không trùng các đỉnh của hình vuông ) .
a, Cm : △BIO=△CMO và tính diện tích tứ giác BIOM theo a.
b, Gọi N là giao đểm của tia AM và tia DC ,K là giao điểm của BN và tia OM . CM : tứ giác IMNB là hình thang và \(\widehat{BKM}=\widehat{BCO.}\)
Cho hình chóp tứ giác đều S.ABCD có các cạnh đều bằng a 2 . Tính thể tích của khối nón có đỉnh S và đường tròn đáy là đường tròn nội tiếp tứ giác ABCD.
A. V = πa 3 2
B. 2 πa 3 6
C. πa 3 6
D. 2 πa 3 2
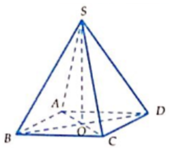
Cho hình chóp tứ giác đều S.ABCD có các cạnh bằng a 2 . Tính thể tích V của khối nón có đỉnh S và đường tròn đáy là đường tròn nội tiếp tứ giác ABCD?
A. V = πa 3 2
B. V = πa 3 2 6
C. V = πa 3 6
D. V = πa 3 2 2
Cho hình chóp tứ giác đều S.ABCD có các cạnh đều bằng 2a. Tính thể tích V của khối nón S có đỉnh và đường tròn đáy là đường tròn nội tiếp tứ giác ABCD.
A. V = π 3 a 3 6
B. V = π 2 a 3 3
C. V = π 2 a 3 6
D. V = π 3 a 3 3
Đáp án B

Bán kính đáy của nón bằng bán kính đường tròn nội tiếp hình vuông ABCD suy ra r = A D 2 = a ; H A = A C 2 = a 2
Chiều cao nón:
h = S A 2 − H A 2 = 4 a 2 − a 2 2 = a 2
Do đó V = π r 2 h 3 = π 2 a 3 3
Cho hình tứ giác ABCD có góc đỉnh A và góc đỉnh D là các góc vuông
a) Hãy vẽ đường thẳng đi qua B và song song với cạnh AD, cắt cạnh DC tại điểm E.
b) Dùng ê ke kiểm tra xem góc đỉnh E của hình tứ giác BEDA có góc vuông hay không?
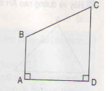
- Học sinh dùng ê – ke vẽ như hình dưới
- Học sinh dùng ê – ke để kiểm tra sẽ thấy góc đỉnh E của tứ giá BEDA là góc vuông
Nói thêm: Góc đỉnh B của tứ giác đó cũng là góc vuông. Tứ giác ABDA là hình chữ nhật
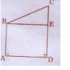
Cho hình tứ giác ABCD có góc đỉnh A và góc đỉnh D là các góc vuông
a) Hãy vẽ đường thẳng đi qua B và song song với cạnh AD, cắt cạnh DC tại điểm E.
b) Dùng ê ke kiểm tra xem góc đỉnh E của hình tứ giác BEDA có góc vuông hay không?
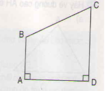
- Học sinh dùng ê – ke vẽ như hình dưới
- Học sinh dùng ê – ke để kiểm tra sẽ thấy góc đỉnh E của tứ giá BEDA là góc vuông
Nói thêm: Góc đỉnh B của tứ giác đó cũng là góc vuông. Tứ giác ABDA là hình chữ nhật
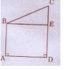
a) Quan sát Hình 20 và cho biết các điểm M, N thuộc hay không thuộc đường thẳng a.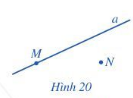
b) Chọn kí hiệu "∈", "∉" thích hợp cho ?:
N ? a; M ? a.
a) Điểm M thuộc đường thẳng a.
Điểm N không thuộc đường thẳng a.
b) N ∉ a.
M ∈ a.
Tứ giác abcd có bốn đỉnh thuộc đường tròn (o) có a =80 b=70 thì số đo của (c) và (d) lần lượt là
góc C=180-80=100 độ
góc D=180-70=110 độ
Cho tứ giác ABCD có hai đỉnh B và C ở trên nửa đường tròn đường kính AD,tâm O.Hai đường chéo AC và BD cắt nhau tại E.Gohi H là hình chiếu vuông góc của E xuống AD và I là trung điểm của DE.cmr
a,Các tứ giác ABEH,DCEH nội tiếp được đường tròn
b,E là tâm đường tròn nội tiếp tam giác BCH
Năm điêm B,C,I,O,H cùng thuộc 1 đường tròn
Ai giúp t câu 3 vs
Để chứng minh 5 điểm trên cùng thuộc một đường tròn, ta chứng minh góc BCH = góc BIH = góc BOH.
Thật vậy, theo chứng minh b, E là tâm đường tròn nội tiếp tam giác BCH nên CE là phân giác góc BCH. Từ đó góc BCH = 2 góc BCA.
Ta có góc BCA bằng góc BDA vì cùng chắn cung BA, nên góc BCH = 2 góc BDA (1)
Tam giác OBD cân tại O nên BOH = 2 góc BDA.(2)
Tam giác EHD vuông tại H , HI là trung tuyến ứng với cạnh huyền nên IH = ID, từ đó góc BIH = 2 góc BDA.(3)
Từ (1), (2), (3) ta suy ra 3 góc trên bằng nhau hay 5 điểm B, C, I, O, H cùng thuộc một đường tròn.