Cho tứ giác ABCD nội tiếp một đường tròn có \(\widehat{A}-\widehat{C}=100^o\).Khẳng định nào dưới đây là đúng?
A. \(\widehat{A}=80^o\). B. \(\widehat{C}=80^o\); C. \(\widehat{B}+\widehat{D}=100^o\). D. \(\widehat{A}=140^o\).
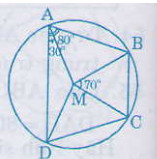
Cho ABCD là một tứ giác nội tiếp đường tròn tâm M, biết \(\widehat{DAB}=80^o,\widehat{DAM}=30^o;\widehat{BMC}=70^o.\)
Hãy tính số đo các góc \(\widehat{MAB};\widehat{BCM};\widehat{AMB};\widehat{DMC};\widehat{AMD};\widehat{MCD}\) và \(\widehat{BCD}.\)
Ta có: =
-
= 80o – 30o = 50o (1)
- ∆MBC là tam giác cân (MB= MC) nên =
= 55o (2)
- ∆MAB là tam giác cân (MA=MB) nên = 50o (theo (1))
Vậy = 180o – 2. 50o = 80o
=
sđcung BCD (số đo góc nội tiếp bằng nửa số đo của cung bị chắn)
=> sđ cung BCD = 2 = 2. 80o = 160o
Mà sđ cung BC = = 70o (số đo ở tâm bằng số đo cung bị chắn)
Vậy cung DC = 160o – 70o = 90o (vì C nằm trên cung nhỏ cung BD)
Suy ra = 90o (4)
∆MAD là tam giác cân (MA= MD)
Suy ra = 180o – 2.30o = 120o (5)
∆MCD là tam giác vuông cân (MC= MD) và = 90o
Suy ra =
= 45o (6)
= 100o theo (2) và (6) và vì CM là tia nằm giữa hai tia CB, CD

Ta có: =
-
= 80o – 30o = 50o (1)
- ∆MBC là tam giác cân (MB= MC) nên =
= 55o (2)
- ∆MAB là tam giác cân (MA=MB) nên = 50o (theo (1))
Vậy = 180o – 2. 50o = 80o
=
sđcung BCD (số đo góc nội tiếp bằng nửa số đo của cung bị chắn)
=> sđ cung BCD = 2 = 2. 80o = 160o
Mà sđ cung BC = = 70o (số đo ở tâm bằng số đo cung bị chắn)
Vậy cung DC = 160o – 70o = 90o (vì C nằm trên cung nhỏ cung BD)
Suy ra = 90o (4)
∆MAD là tam giác cân (MA= MD)
Suy ra = 180o – 2.30o = 120o (5)
∆MCD là tam giác vuông cân (MC= MD) và = 90o
Suy ra =
= 45o (6)
= 100o theo (2) và (6) và vì CM là tia nằm giữa hai tia CB, CD
Cho tứ giác ABCD có: AB=BC;CD=DA.
a) C/m BD là đường trung trực của AC
b) Cho \(\widehat{B}=100^{\sigma},\widehat{D}=80^{\sigma}\) .Tính \(\widehat{A}\) và \(\widehat{C}\).
a) BA=BC(gt)
⇒B thuộc đường trung trực AC
DA=DC(gt)
⇒D thuộc đường trung trực AC
B và D là đường phân biệt cùng thuộc 1 đường trung trực AC nên đường thẳng BD là đường trung trực của AC
b) Xét △BAD và △BCD,có:
BA=BC
DA=DC
BC chung
⇒△BAD=△BCD(ccc)⇒góc BAD= góc BCD
Ta có BAD+BCD+ABC+ADC=360
2BAD=360-ABC-ADC
2BAD=360-100-80
2BAD=180
⇒BAD=BCD=180/2=80
Cho tứ giác ABCD có AB= BC; CD = DA
a) Chứng minh BD là đường trung trức của AC
b) Cho \(\widehat{B}\) = 100 độ, \(\widehat{D}\)= 80 độ. Tính \(\widehat{A}\) và \(\widehat{C}\)
a) Ta có : AB=BC và CD=DA (đề bài)
⇒ BD là đường trung trực của AC
b) Ta có : AB=BC (đề bài)
⇒ Δ ABC cân tại B
⇒ Góc BAC = Góc BCA
Tương tự ta chứng minh Góc DAC = Góc DCA (CD=AD...)
mà Góc A = Góc BAC + Góc DAC
Góc C = Góc BCA+ Góc DCA
⇒ Góc A = Góc C
mà A + B + C +D =360; B=100o ; D=80o
⇒ A + C =360 - (100 + 80) = 240
⇒ A = C = 240 : 2 = 120o
a, Cho tam giác ABC biết \(\widehat{A}=100^o,\widehat{B}-\widehat{C}=50^o.Tính\widehat{B},\widehat{C}\)
b, Tam giác ABC có\(\widehat{B}=80^o,3\widehat{A}=2\widehat{C}.Tính\widehat{A},\widehat{C}\)
a)
=> Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}\) = 180o
100o + \(\widehat{B}+\widehat{C}\) = 180o
\(\widehat{B}+\widehat{C}\) = 180o - 100o
\(\widehat{B}+\widehat{C}\) = 80o
Góc B = (80o+50o):2 = 65o
=> \(\widehat{C}\) = 65o - 50o = 15o
Vậy \(\widehat{B}\) = 65o ; \(\widehat{C}\) = 15o
b)
Ta có : \(\widehat{3A}+\widehat{B}+\widehat{2C}\) = 180o
\(\widehat{3A}+\widehat{2C}\) = 180o - 80o
\(\widehat{3A}+\widehat{2C}\) = 100o
=> \(\widehat{A}\) = 100o:(3+2).3 = 60o
\(\widehat{C}\) = 100o - 60o = 40o
Vậy \(\widehat{A}\) = 60o ; \(\widehat{C}\) = 40o
Cho tứ giác ABCD nội tiếp đường tròn (O) có AB = BD. Các đường thẳng AB và DC cắt nhau tại N, đường thẳng CB cắt tiếp tuyến tại A của đường tròn (O) tại M. Chứng minh \(\widehat{AMN}=\widehat{ABD}\)
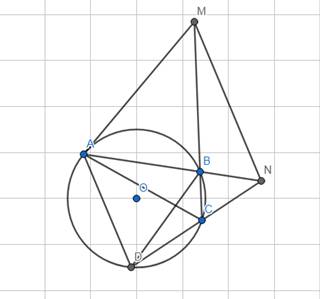
*Chứng minh AMNC là tứ giác nội tiếp.
Ta có AB=BD nên △ABD cân tại B.
\(\Rightarrow\widehat{ADB}=\widehat{BAD}\left(1\right)\)
Trong (O) có: \(\widehat{MAB}\) là góc tạo bởi tiếp tuyến và dây cung chắn cung AB.
\(\widehat{ADB}\) là góc nội tiếp chắn cung AB.
\(\Rightarrow\widehat{MAB}=\widehat{ADB}\left(2\right)\)
Tứ giác ABCD nội tiếp có \(\widehat{BCN}\) là góc ngoài ở đỉnh C.
\(\Rightarrow\widehat{BCN}=\widehat{BAD}\left(3\right)\)
(1), (2), (3) \(\Rightarrow\widehat{MAB}=\widehat{BCN}\).
\(\Rightarrow\)AMNC nội tiếp.
*Chứng minh yêu cầu đề bài.
AMNC nội tiếp \(\Rightarrow\widehat{AMN}=\widehat{ACD}\) (\(\widehat{ACD}\) là góc ngoài ở đỉnh C).
Mà \(\widehat{ACD}=\widehat{ABD}\) (ABCD nội tiếp)
\(\Rightarrow\widehat{AMN}=\widehat{ABD}\) (đpcm)
Tứ giác ABCD có \(\widehat{B}=\widehat{A}+10^0;\widehat{C}=\widehat{B}+10^0;\widehat{D}=\widehat{C}+10^0\). Khẳng định nào dưới đây là đúng ?
(A) \(\widehat{A}=65^0\) (B) \(\widehat{B}=85^0\) (C) \(\widehat{C}=100^0\) (D) \(\widehat{D}=90^0\)
Ta có:
\(\widehat{B}=\widehat{A}+10^o \)(1)
\(\widehat{C}=\widehat{B}+10^o\)(2)
\(\widehat{D}=\widehat{C}+10^o\)(3)
Cộng cả hai vế của (1) với (2) và (3) ta có:
\(\widehat{B}+\widehat{C}+\widehat{D}=\widehat{A}+\widehat{B}+\widehat{C}+30^o\)
\(\Rightarrow\)\(\widehat{B}+\widehat{C}+\widehat{D}-\widehat{A}+\widehat{B}+\widehat{C}=30^o\)
\(\Leftrightarrow\)\(\widehat{D}-\widehat{A}=30^o\)
\(\Rightarrow\)\(\widehat{A}=75^o\)
\(\Rightarrow\)\(\widehat{B}=85^o\)
Vậy khẳng định B là đúng
Cho hình chữ nhật ABCD nội tiếp đường tròn tâm O. Trên cung nhỏ AB lấy điểm E ( E ko trùng A và B), F là giao của AB và CE.
a) CM tứ giác FBHE nội tiếp
b) CM \(\widehat{FHA}=\widehat{ADE}\) ???
Cho tứ giác ABCD, biết: \(\widehat{B}=\widehat{A}+20^o;\widehat{C}=3\widehat{A};\widehat{D}-\widehat{C}=20^o\).
a) Tính các góc của tứ giác ABCD
b) Tứ giác ABCD có phải hình thang không? Vì sao?
Cho tứ giác ABCD có \(\widehat A = {60^o},\widehat B = {70^o},\widehat C = {80^o}\). Khi đó, \(\widehat D\) bằng:
A. 130o
B. 140o
C. 150o
D. 160o
ABCD là tứ giác nên:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\\ \Rightarrow \widehat D = {360^o} - \widehat A - \widehat B - \widehat C = {360^o} - {60^o} - {70^o} - {80^o} = {150^o}\end{array}\)
Chọn đáp án C
Cho tam giác ABC có \(\widehat{A}>\widehat{B}>\widehat{C}\) nội tiếp trong đường tròn (O), ngoại tiếp đường tròn (I). Cung nhỏ BC có M là điểm chính giữa. N là trung điểm của cạnh BC. Điểm E đối xứng với I qua N. Đường thẳng ME cắt đường tròn (O) tại điểm thứ hai là Q. Lấy điểm K thuộc BQ sao cho QK=QA. Chứng minh:
a) Điểm Q thuộc cung nhỏ AC của đường tròn (O)
b)Tứ giác AIKB nội tiếp và BQ=AQ+CQ