Question

Cho ABCD là một tứ giác nội tiếp đường tròn tâm M, biết \(\widehat{DAB}=80^o,\widehat{DAM}=30^o;\widehat{BMC}=70^o.\)

Hãy tính số đo các góc \(\widehat{MAB};\widehat{BCM};\widehat{AMB};\widehat{DMC};\widehat{AMD};\widehat{MCD}\) và \(\widehat{BCD}.\)

Answer 1

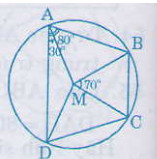
Ta có: = - = 80^o – 30^o = 50^o (1)

- ∆MBC là tam giác cân (MB= MC) nên = = 55^o (2)

- ∆MAB là tam giác cân (MA=MB) nên = 50^o (theo (1))

Vậy = 180^o – 2. 50^o = 80^o

= sđcung BCD (số đo góc nội tiếp bằng nửa số đo của cung bị chắn)

=> sđ cung BCD = 2 = 2. 80^o = 160^o

Mà sđ cung BC = = 70^o (số đo ở tâm bằng số đo cung bị chắn)

Vậy cung DC = 160^o – 70^o = 90^o (vì C nằm trên cung nhỏ cung BD)

Suy ra = 90^{o (4)}

∆MAD là tam giác cân (MA= MD)

Suy ra = 180^o – 2.30^o = 120^o (5)

∆MCD là tam giác vuông cân (MC= MD) và = 90^o

Suy ra = = 45^o (6)

= 100^o theo (2) và (6) và vì CM là tia nằm giữa hai tia CB, CD

Answer 2

Ta có: = - = 80^o – 30^o = 50^o (1)

- ∆MBC là tam giác cân (MB= MC) nên = = 55^o (2)

- ∆MAB là tam giác cân (MA=MB) nên = 50^o (theo (1))

Vậy = 180^o – 2. 50^o = 80^o

= sđcung BCD (số đo góc nội tiếp bằng nửa số đo của cung bị chắn)

=> sđ cung BCD = 2 = 2. 80^o = 160^o

Mà sđ cung BC = = 70^o (số đo ở tâm bằng số đo cung bị chắn)

Vậy cung DC = 160^o – 70^o = 90^o (vì C nằm trên cung nhỏ cung BD)

Suy ra = 90^{o (4)}

∆MAD là tam giác cân (MA= MD)

Suy ra = 180^o – 2.30^o = 120^o (5)

∆MCD là tam giác vuông cân (MC= MD) và = 90^o

Suy ra = = 45^o (6)

= 100^o theo (2) và (6) và vì CM là tia nằm giữa hai tia CB, CD