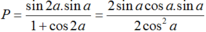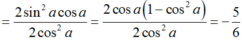Tính giá trị biểu thức
\(cos^218.sin^236-cos36sin18\)
Không dùng máy tính rút gọn biểu thức và tính giá trị
\(H=cot15^o.cot35^o.cot55^o.cot75^o\\ I=tan10^o.tan20^o.tan30^o....tan80^o\\ K=sin^228^o+sin^236^o+sin^254^o+cos^2152^o\)
\(H=cot15^o.cot35^o.cot55^o.cot75^o\)
\(=\left(cot15^o.cot75^o\right).\left(cot35^o.cot55^o\right)\)
\(=\left(cot15^o.tan15^o\right).\left(cot35^o.tan35^o\right)\)
\(=1\)
\(I=tan10^o.tan20^o.tan30^o....tan80^o\)
\(=\left(tan10^o.cot10^o\right).\left(tan20^o.cot20^o\right).\left(tan30^o.cot30^o\right).\left(tan40^o.cot40^o\right)\)
\(=1\)
Cho cos x + sin x = 3/4. Tính giá trị biểu thức A= |sin x - cos x|
Ta có \(2\sin x\cos x=\left(\sin x+\cos x\right)^2-\left(\sin^2x+\cos^2x\right)\)
\(=\left(\dfrac{3}{4}\right)^2-1=-\dfrac{7}{16}\)
Từ đó \(A=\left|\sin x-\cos x\right|\)
\(\Rightarrow A^2=\left(\sin x-\cos x\right)^2\)
\(A^2=\sin^2x+\cos^2x-2\sin x\cos x\)
\(A^2=1+\dfrac{7}{16}=\dfrac{23}{16}\)
\(\Rightarrow A=\dfrac{\sqrt{23}}{4}\) (do \(A\ge0\))
Có \(\cos x+\sin x=\dfrac{3}{4}\)
\(\Leftrightarrow\left(\cos x+\sin x\right)^2=\dfrac{9}{16}\)
\(\Leftrightarrow2.\sin x.\cos x+1=\dfrac{9}{16}\)
\(\Leftrightarrow\sin x.\cos x=-\dfrac{7}{32}\)
Lại có \(\left(\cos x+\sin x\right)^2=\left(\cos x-\sin x\right)^2+4.\sin x.\cos x=\dfrac{9}{16}\)
\(\Leftrightarrow\left(\cos x-\sin x\right)^2=\dfrac{23}{16}\)
\(\Leftrightarrow\left|\sin x-\cos x\right|=\dfrac{\sqrt{23}}{4}\)
Cho cos α = 1 3 . Tính giá trị của biểu thức P = sin 3 a - sin a sin 2 a
![]()
![]()

![]()
Chọn A.
Áp dụng công thức biến đổi tổng thành tích và công thức nhân đôi; ta có
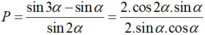

Tính giá trị của biểu thức:
\(A=\frac{3\cos67^0}{2\tan23^0}-\frac{\cos^236^0+\cos^254^0-\cos^217^0-\cos^273^0}{\sin^224^0+\sin^266^0+\sin^215^0+\sin^275^0}\)
Biết cot α=\(\sqrt{5}\). Tính giá trị biểu thức: A=\(\dfrac{\sin^2\alpha+\cos^2\alpha}{\sin\alpha.\cos\alpha}\)
Ta có: \(cot\alpha=\dfrac{cos\alpha}{sin\alpha}=\dfrac{cos^2\alpha}{sin\alpha.cos\alpha}=\sqrt{5}\)
Lại có: \(\dfrac{1}{cot\alpha}=tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{sin^2\alpha}{cos\alpha.sin\alpha}=\dfrac{1}{\sqrt{5}}\)
\(\Rightarrow A=\dfrac{cos^2\alpha}{sin\alpha.cos\alpha}+\dfrac{sin^2\alpha}{sin\alpha.cos\alpha}=\sqrt{5}+\dfrac{1}{\sqrt{5}}=\dfrac{6}{\sqrt{5}}=\dfrac{6\sqrt{5}}{5}\)
Ta có : cot α = \(\sqrt{5}\Rightarrow\dfrac{cos\alpha}{sin\alpha}=\sqrt{5}\Rightarrow cos\alpha=\sqrt{5}.sin\alpha\)
\(A=\dfrac{sin^2\alpha+cos^2\alpha}{sin\alpha.cos\alpha}\)
\(A=\dfrac{sin^2\alpha+\left(\sqrt{5}sin\alpha\right)^2}{sin\alpha.\sqrt{5}sin\alpha}=\dfrac{sin^2\alpha+5sin^2\alpha}{\sqrt{5}sin^2\alpha}\)
\(A=\dfrac{6sin^2\alpha}{\sqrt{5}sin^2\alpha}=\dfrac{6}{\sqrt{5}}=\dfrac{6\sqrt{5}}{5}\)
Tính giá trị của biểu thức biết tanα=-2
\(\dfrac{2\sin\alpha+\cos\alpha}{2\sin^3\alpha-\cos^3\alpha}\)
\(\dfrac{2sina+cosa}{2sin^3a-cos^3a}=\dfrac{\dfrac{2sina}{cos^3a}+\dfrac{cosa}{cos^3a}}{\dfrac{2sin^3a}{cos^3a}-\dfrac{cos^3a}{cos^3a}}=\dfrac{2tana.\dfrac{1}{cos^2a}+\dfrac{1}{cos^2a}}{2tan^3a-1}\)
\(=\dfrac{2tana\left(1+tan^2a\right)+1+tan^2a}{2tan^3a-1}=...\) (thay số và bấm máy)
Cho \(\tan\alpha=\dfrac{3}{5}\). Tính giá trị của các biểu thức sau:
M=\(\dfrac{\sin\alpha+\cos\alpha}{\sin\alpha-\cos\alpha}\)
N=\(\dfrac{\sin\alpha\times\cos\alpha}{\sin^2\alpha-\cos^2\alpha}\)
Lời giải:
\(M=\frac{\frac{\sin a}{\cos a}+1}{\frac{\sin a}{\cos a}-1}=\frac{\tan a+1}{\tan a-1}=\frac{\frac{3}{5}+1}{\frac{3}{5}-1}=-4\)
\(N = \frac{\frac{\sin a\cos a}{\cos ^2a}}{\frac{\sin ^2a-\cos ^2a}{\cos ^2a}}=\frac{\frac{\sin a}{\cos a}}{(\frac{\sin a}{\cos a})^2-1}=\frac{\tan a}{\tan ^2a-1}=\frac{\frac{3}{5}}{\frac{3^2}{5^2}-1}=\frac{-15}{16}\)
Tính giá trị của biểu thức P = sin 2 α . sin α 1 + cos 2 α biết cos α = - 2 3
![]()
![]()
![]()
![]()
Chọn D.
Ta có : sin2a = 2.sina. cosa và sin2a = 1 - cos2a.
Do đó;