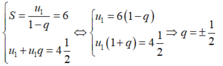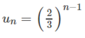tìm dạng khai triển của cấp số nhân lùi vô hạn biết tổng = 32, U2 = 8

Những câu hỏi liên quan
tìm dạng khai triển của cấp số nhân lùi vô hạn Un, biết tổng bằng 32, U2= 8
\(\dfrac{u_2}{q\left(1-q\right)}=32\rightarrow\dfrac{8}{q\left(1-q\right)}=32\rightarrow q=\dfrac{1}{2}\rightarrow u_1=16\\ \rightarrow u_n=16\left(\dfrac{1}{2}\right)^{n-1}=2^{5-n}\)
Đúng 0
Bình luận (0)
Cho cấp số nhân lùi vô hạn, biết tổng S 6 và tổng hai số hạng đầu
u
1
+
u
2
4
1
2
Tìm công bội của cấp số nhân đó? A.
q
±
1
3
B.
q
±
1
2
C.
q
±
1
2
D. Đáp án khác
Đọc tiếp
Cho cấp số nhân lùi vô hạn, biết tổng S= 6 và tổng hai số hạng đầu u 1 + u 2 = 4 1 2
Tìm công bội của cấp số nhân đó?
A. q = ± 1 3
B. q = ± 1 2
C. q = ± 1 2
D. Đáp án khác
a. Có nhận xét gì về công bội của các cấp số nhân lùi vô hạn?
b. Cho ví dụ về một cấp số nhân lùi vô hạn và có công bội là số âm và một cấp số nhân lùi vô hạn có công bội là số dương và tính tổng của các cấp số nhân đó.
a) Cấp số nhân vô hạn với công bội q mà |q| < 1 là cấp số nhân lùi vô hạn
b) Ví dụ về cấp số nhân lùi vô hạn có công bội âm:
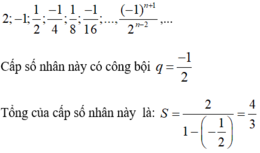

Đúng 0
Bình luận (0)
a) Có nhận xét gì về công bội của các cấp số nhân lùi vô hạn ?
b) Cho ví dụ về một cấp số nhân lùi vô hạn có công bội là số âm và một cấp số nhân lùi vô hạn có công bội là số dương và tính tổng của mỗi cấp số nhân đó ?
Một cấp số nhân lùi vô hạn có tổng bằng S. Biết số hạng thứ hai của cấp số nhân đó bằng 1. Tìm giá trị nhỏ nhất có thể của S A.
1
+
5
2
B. 3 C. 4 D.
5
Đọc tiếp
Một cấp số nhân lùi vô hạn có tổng bằng S. Biết số hạng thứ hai của cấp số nhân đó bằng 1. Tìm giá trị nhỏ nhất có thể của S
A. 1 + 5 2
B. 3
C. 4
D. 5
Đáp án C.
Gọi q là công sai của cấp số nhân. Vì u 2 = 1 nên suy ra u 1 = u 2 q = 1 q .
Ta có
S = u 1 1 − q = 1 q 1 − q = 1 q 1 − q , q < 1
Ta có a − b 2 ≥ 0 ⇔ a 2 + b 2 ≥ 2 a b ⇔ a + b 2 4 ≥ a b (với mọi a ; b ∈ ℝ ).
Áp dụng bất đẳng thức vừa chứng minh ở trên ta có q 1 − q ≤ q + 1 − q 2 4 = 1 4 ⇔ 1 q 1 − q ≥ 4 ⇔ S ≥ 4
Dấu bằng xảy ra khi q = 1 2 .
Vậy giá trị nhỏ nhất của S là 4 khi q = 1 2 .
Đúng 0
Bình luận (0)
Cho cấp số nhân lùi vô hạn
u
n
có công bội q. Khi đó tổng của cấp số nhân lùi vô hạn đó được tính bởi công thức nào sau đây: A.
S
1
1
-
q
B.
S
u
1
1
-
q
C.
S...
Đọc tiếp
Cho cấp số nhân lùi vô hạn u n có công bội q. Khi đó tổng của cấp số nhân lùi vô hạn đó được tính bởi công thức nào sau đây:
A. S = 1 1 - q
B. S = u 1 1 - q
C. S = u 1 1 + q n
D. S = u 1 1 - q n
Đáp án B
- Cách giải:
Cho cấp số nhân lùi vô hạn
u
n
có công bội q. Khi đó tổng của cấp số nhân lùi vô hạn đó được tính bởi công thức 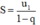
Đúng 0
Bình luận (0)
a) Tính tổng của cấp số nhân lùi vô hạn (un), với u1=\(\dfrac{2}{3}\),q=−\(\dfrac{1}{4}\)
b) Biểu diễn số thập phân vô hạn tuần hoàn 1,(6) dưới dạng phân số
a: \(S=\dfrac{\dfrac{2}{3}}{\dfrac{5}{4}}=\dfrac{8}{15}\)
b: 1,(6)=5/3
Đúng 0
Bình luận (0)
a) Tính tổng của cấp số nhân lùi vô hạn \(\left( {{u_n}} \right),\) với \({u_1} = \frac{2}{3},q = - \frac{1}{4}.\)
b) Biểu diễn số thập phân vô hạn tuần hoàn 1,(6) dưới dạng phân số.
a) \(S = \frac{{{u_1}}}{{1 - q}} = \frac{{\frac{2}{3}}}{{1 - \frac{{ - 1}}{4}}} = \frac{8}{{15}}\)
b) \(1,\left( 6 \right) = \frac{5}{3}\)
Đúng 0
Bình luận (0)
Tìm số hạng tổng quát của cấp số nhân lùi vô hạn có tổng bằng 3 và công bội q = 2/3