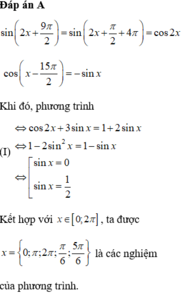1.

\(sin^3x+cos^3x=1-\dfrac{1}{2}sin2x\)

\(\Leftrightarrow\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)=1-sinx.cosx\)

\(\Leftrightarrow\left(sinx+cosx\right)\left(1-sinx.cosx\right)=1-sinx.cosx\)

\(\Leftrightarrow\left(1-sinx.cosx\right)\left(sinx+cosx-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinx.cosx=1\\sinx+cosx=1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}sin2x=2\left(vn\right)\\\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\end{matrix}\right.\)

\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\)

\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{4}=\pi-\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)

2.

\(\left|cosx-sinx\right|+2sin2x=1\)

\(\Leftrightarrow\left|cosx-sinx\right|-1+2sin2x=0\)

\(\Leftrightarrow\left|cosx-sinx\right|-\left(cosx-sinx\right)^2=0\)

\(\Leftrightarrow\left|cosx-sinx\right|\left(1-\left|cosx-sinx\right|\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)=0\\\left|cosx-sinx\right|=1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=k\pi\\cos^2x+sin^2x-2sinx.cosx=1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\1-sin2x=1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\sin2x=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{k\pi}{2}\end{matrix}\right.\)

3.

\(2sin2x-3\sqrt{6}\left|sinx+cosx\right|+8=0\)

\(\Leftrightarrow2\left(sinx+cosx\right)^2-3\sqrt{6}\left|sinx+cosx\right|+6=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\left|sinx+cosx\right|=\sqrt{6}\left(vn\right)\\\left|sinx+cosx\right|=\dfrac{\sqrt{6}}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left|sin\left(x+\dfrac{\pi}{4}\right)\right|=\dfrac{\sqrt{3}}{2}\)

\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\pm\dfrac{\sqrt{3}}{2}\)

...

\(sin^3x+cos^3x-sinx-cosx=cos2x\)

\(\Leftrightarrow\left(sinx+cosx\right)\left(sin^2x-sinx.cosx+cos^2x\right)-\left(sinx+cosx\right)-\left(cos^2x-sin^2x\right)\)\(=0\)

​​\(\Leftrightarrow\left(sinx+cosx\right)\left(1-sinx.cosx\right)-\left(sinx+cosx\right)-\left(cosx+sinx\right)\left(cosx-sinx\right)=0\)​​

\(\Leftrightarrow\left(sinx+cosx\right)\left(sinx-cosx-sinx.cosx\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=0\left(1\right)\\sinx-cosx-sinx.cosx=0\left(2\right)\end{matrix}\right.\)

TH1: (1)\(\Leftrightarrow\sqrt{2}.sin\left(x+\dfrac{\pi}{4}\right)=0\)\(\Leftrightarrow x=-\dfrac{\pi}{4}+k\pi\left(k\in Z\right)\)

TH2: Đặt \(t=sinx-cosx\) ;\(t\in\left(-2;2\right)\)

\(\Rightarrow\dfrac{t^2-1}{2}=-sinx.cosx\)

Pt (2)\(\Rightarrow t+\dfrac{t^2-1}{2}=0\)\(\Leftrightarrow t^2+2t-1=0\) \(\Leftrightarrow\left[{}\begin{matrix}t=-1+\sqrt{2}\left(tm\right)\\t=-1-\sqrt{2}\left(ktm\right)\end{matrix}\right.\)

\(\Rightarrow sinx-cosx=-1+\sqrt{2}\)\(\Leftrightarrow\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)=-\sqrt{2}+1\)

\(\Leftrightarrow cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{1-\sqrt{2}}{\sqrt{2}}\)

\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+arc.cos\dfrac{1-\sqrt{2}}{2}+k2\pi\\x=\dfrac{-\pi}{4}-arc.cos\dfrac{1-\sqrt{2}}{2}+k2\pi\end{matrix}\right.\)(\(k\in\)\(Z\))

Vậy...

a, (sinx + cosx)(1 - sinx . cosx) = (cosx - sinx)(cosx + sinx)

⇔ \(\left[{}\begin{matrix}sinx+cosx=0\\cosx-sinx=1-sinx.cosx\end{matrix}\right.\)

⇔ \(\left[{}\begin{matrix}sinx+cosx=0\\cosx+sinx.cosx-1-sinx=0\end{matrix}\right.\)

⇔ \(\left[{}\begin{matrix}sinx+cosx=0\\\left(cosx-1\right)\left(sinx+1\right)=0\end{matrix}\right.\)

⇔ \(\left[{}\begin{matrix}sin\left(x+\dfrac{\pi}{4}\right)=0\\cosx=1\\sinx=-1\end{matrix}\right.\)

b, (sinx + cosx)(1 - sinx . cosx) = 2sin2x + sinx + cosx

⇔ (sinx + cosx)(1 - sinx.cosx - 1) = 2sin2x

⇔ (sinx + cosx).(- sinx . cosx) = 2sin2x

⇔ 4sin2x + (sinx + cosx) . sin2x = 0

⇔ \(\left[{}\begin{matrix}sin2x=0\\\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+4=0\end{matrix}\right.\)

⇔ sin2x = 0

c, 2cos³x = sin3x

⇔ 2cos³x = 3sinx - 4sin³x

⇔ 4sin³x + 2cos³x - 3sinx(sin²x + cos²x) = 0

⇔ sin³x + 2cos³x - 3sinx.cos²x = 0

Xét cosx = 0 : thay vào phương trình ta được sinx = 0. Không có cung x nào có cả cos và sin = 0 nên cosx = 0 không thỏa mãn phương trình

Xét cosx ≠ 0 chia cả 2 vế cho cos³x ta được : 

tan³x + 2 - 3tanx = 0

⇔ \(\left[{}\begin{matrix}tanx=1\\tanx=-2\end{matrix}\right.\)

d, cos²x - \(\sqrt{3}sin2x\) = 1 + sin²x

⇔ cos²x - sin²x - \(\sqrt{3}sin2x\) = 1

⇔ cos2x - \(\sqrt{3}sin2x\) = 1

⇔ \(2cos\left(2x+\dfrac{\pi}{3}\right)=1\)

⇔ \(cos\left(2x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}=cos\dfrac{\pi}{3}\)

e, cos³x + sin³x = 2cos⁵x + 2sin⁵x

⇔ cos³x (1 - 2cos²x) + sin³x (1 - 2sin²x) = 0

⇔ cos³x . (- cos2x) + sin³x . cos2x = 0

⇔ \(\left[{}\begin{matrix}sin^3x=cos^3x\\cos2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}sinx=cosx\\cos2x=0\end{matrix}\right.\)

⇔ \(\left[{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)=0\\cos2x=0\end{matrix}\right.\)

1: =>sin^2(3x)=0

=>sin 3x=0

=>3x=kpi

=>x=kpi/3

2:

\(sinx=1-cos^2x=sin^2x\)

=>\(sin^2x-sinx=0\)

=>sin x(sin x-1)=0

=>sin x=0 hoặc sin x=1

=>x=pi/2+k2pi hoặc x=kpi

4:

sin 2x+sin x=0

=>sin 2x=-sin x=sin(-x)

=>2x=-x+k2pi hoặc 2x=pi+x+k2pi

=>x=pi+k2pi hoặc x=k2pi/3

5: =>cos(x+pi/3)=1/căn 2

=>x+pi/3=pi/4+k2pi hoặc x+pi/3=-pi/4+k2pi

=>x=-pi/12+k2pi hoặc x=-7/12pi+k2pi

3.

\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sinx-\dfrac{1}{2}cosx=cos3x\)

\(\Leftrightarrow sin\left(x-\dfrac{\pi}{6}\right)=sin\left(\dfrac{\pi}{2}-3x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{6}=\dfrac{\pi}{2}-3x+k2\pi\\x-\dfrac{\pi}{6}=\dfrac{\pi}{2}+3x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\\x=-\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)

câu 2 mình sửa lại đề bài một chút là: sin(cosx)=1 ạ

1.

\(sin\left(sinx\right)=0\)

\(\Leftrightarrow sinx=k\pi\) (1)

Do \(-1\le sinx\le1\Rightarrow-1\le k\pi\le1\)

\(\Rightarrow-\dfrac{1}{\pi}\le k\le\dfrac{1}{\pi}\Rightarrow k=0\) do \(k\in Z\)

Thế vào (1)

\(\Rightarrow sinx=0\Rightarrow x=n\pi\)

2.

\(sin\left(cosx\right)=1\Leftrightarrow cosx=\dfrac{\pi}{2}+k2\pi\)

Do \(-1\le cosx\le1\Rightarrow-1\le\dfrac{\pi}{2}+k2\pi\le1\)

\(\Rightarrow-\dfrac{1}{2\pi}-\dfrac{1}{4}\le k\le\dfrac{1}{2\pi}-\dfrac{1}{4}\) 

\(\Rightarrow\) Không tồn tại k thỏa mãn

Pt vô nghiệm

\(\Leftrightarrow\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)=4\left(sinx+cosx\right)\)

\(\Leftrightarrow\left(sinx+cosx\right)\left(1-sinx.cosx\right)-4\left(sinx+cosx\right)=0\)

\(\Leftrightarrow\left(sinx+cosx\right)\left(-3-\frac{1}{2}sin2x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cosx+sinx=0\\sin2x=-6\left(vn\right)\end{matrix}\right.\)

\(\Rightarrow cosx=-sinx=cos\left(\frac{\pi}{2}+x\right)\)

\(\Rightarrow x=-\frac{\pi}{2}-x+k2\pi\)

\(\Rightarrow x=-\frac{\pi}{4}+k\pi\)

\(0\le-\frac{\pi}{4}+k\pi\le\pi\Rightarrow k=1\)

\(\Rightarrow x=\frac{3\pi}{4}\)

mik lm biếng quá mik chỉ nói cách làm thôi nha bạn

1) chia hai vế cho cos^2(x) \(\sqrt{3}tan^2x+\left(1-\sqrt{3}\right)tanx-1+\left(1-\sqrt{3}\right)\left(1+tan^2x\right)=0\)

đặt t = tanx rr giải thôi =D ( máy 570 thì mode5 3 còn máy 580 thì mode 9 2 2) :)))

2) cx làm cách tương tự chia 2 vế cho cos^2x

3) giữ vế trái bung vế phải ra

\(sin2x-2sin^2x=2-4sin^22x\)

đặt t = sin2x (-1=<t=<1)

4) đẩy sinx cosx qua trái hết

\(sinx\left(sin^2-1\right)-cosx\left(cos^2x+1\right)=0\)

\(sinx\left(-cos^2x\right)-cos\left(cos^2x+1\right)=0\)

\(-cos\left(sinxcosx+cos^2x+1\right)=0\)

cái vế đầu cosx=0 bn bik giả rr mà dễ ẹc à còn vế sau thì chia cho cos^2(x) như mấy bài trên rr sau đó đặt t = tanx rr bấm máy là ra thui :))

5)bung cái hằng đẳng thức ra sau đó đặt t=sinx+cosx (t thuộc [-căn(2) ; căn(2)]

khi đó ta có sinxcosx=1/2 sin2x= 1/2t^2 - 1/2

làm đi là ra à