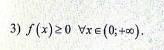
f(x)= x^2-2mx-m+90
Cho hàm số f(x) = 2mx + lnx. Tìm m để nguyên âm F(x) của f(x) thỏa mãn F(1) = 0 và F(2) = 2 +2ln2
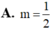
![]()
![]()
![]()
Cho f(x)=x^2+2mx+m+6
Tìm m để f(x) > 0 với mọi x thuộc R
\(f(x)=x^2+2mx+m+6\)
Để $f(x) >0 \forall x \in \mathbb{R}$ thì \(\left\{{}\begin{matrix}1>0\\\Delta'< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\in R\\m^2-\left(m+6\right)< 0\end{matrix}\right.\)\(\Leftrightarrow m^2-m-6< 0\Leftrightarrow-2< m< 3\)
KL: ....................
Cho \(f\left(x\right)=x^2+2mx+2m-3\). Tìm m để f(x)<0 \(\forall x\in\left(-1;2\right)\)
\(\Delta'=m^2-2m+3>0\) ; \(\forall x\)
Do đó bài toán thỏa mãn khi pt \(f\left(x\right)=0\) có 2 nghiệm thỏa mãn: \(x_1< -1< 2< x_2\)
\(\Leftrightarrow\left\{{}\begin{matrix}a.f\left(-1\right)< 0\\a.f\left(2\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}1.\left(1-2m+2m-3\right)< 0\\1\left(4+4m+2m-3\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow6m+1< 0\Rightarrow m< -\dfrac{1}{6}\)
cho f(x) =\(x^4-2mx^2-x+m^2-m=0\)
tìm x để f(x) có 4 nghiệm phân biệt
Cho f(x)=-x2+2mx-2m2-2m-2m. Tìm m sao cho f(x)<0, ∀x∈R.
Cho hai đa thức: f(x)=x2+2mx+m2 và q(x)=x2+(2m+1)x+m2. Tìm m biết f(1)=q(-1).
cho f(x)=x^3+x+(x+1)^2 và g(x)=2mx^2+x-5.
tìm nghiệm của m để f(x) là nghiệm của g(x)
Cho f(x) = x^2 + 2mx + m^2 và Q(x) = x^2 + 3mx + 2m^2 Tìm m biết P(1)=Q(-1)
theo đề bài, ta có:
\(F\left(1\right)=Q\left(-1\right)\\ \Leftrightarrow1+2m+m^2=1-3m+2m^2\\ \Leftrightarrow m^2-5m=0\\ \Leftrightarrow m\left(m-5\right)=0\Rightarrow\left[{}\begin{matrix}m=0\\m=5\end{matrix}\right.\)
vậy F(1)=Q(-1) khi x=0 hoặc 5
Cho 2 đa thức f(x) = x2 + 2mx + m2 và g(x) = x2 + (2m+1)x + m2. Hãy tìm m biết rằng f(1) = g(-1)
Thôi tiện t giúp luôn =)
Vì f(1) = g(-1) nên
\(1+2m+m^2=1+\left(-1\right)\left(2m+1\right)+m^2\)
\(\Leftrightarrow m^2+2m+1=1-2m-1+m^2\)
\(\Leftrightarrow4m=-1\)
\(\Leftrightarrow m=-\frac{1}{4}\)