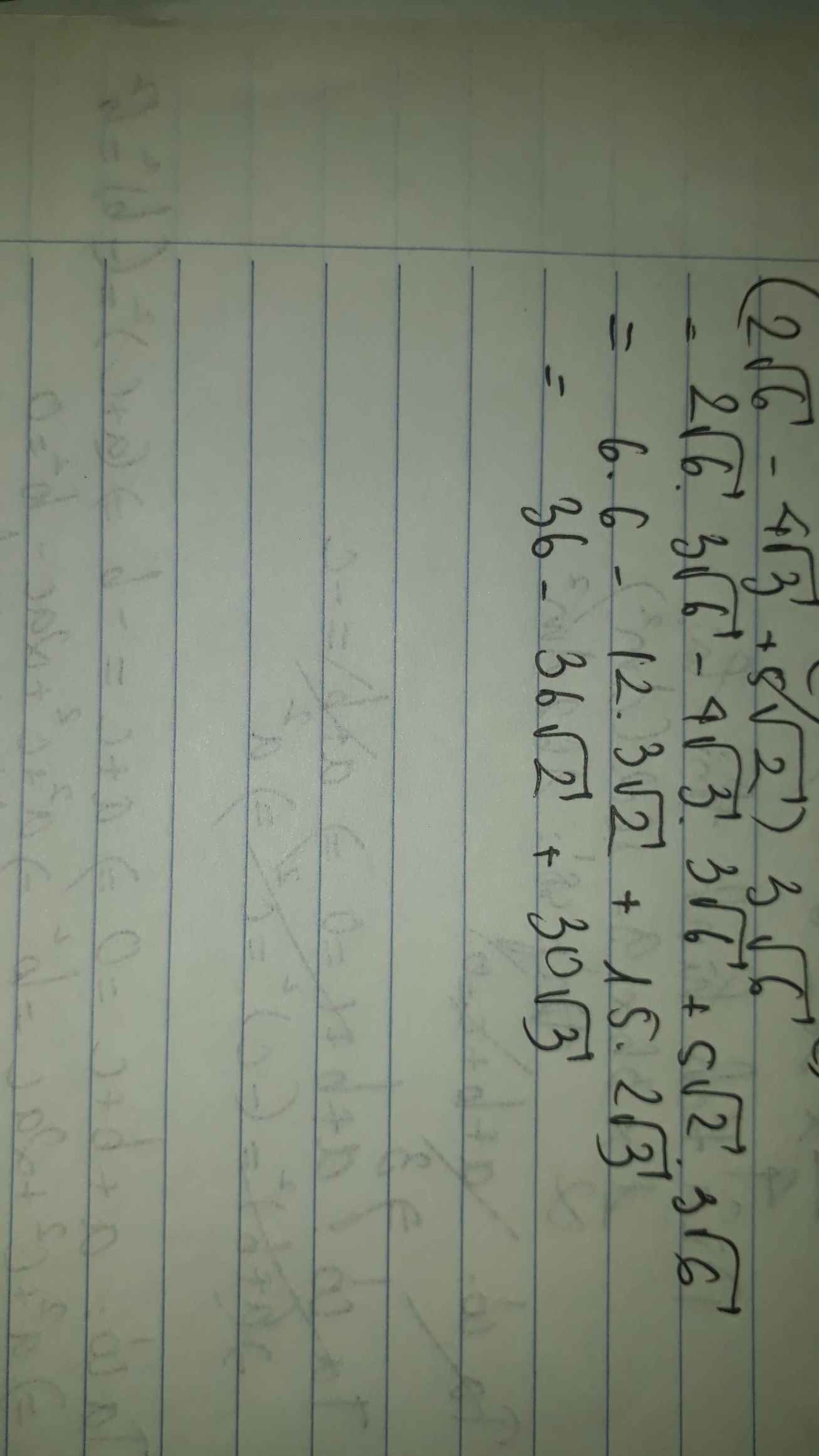\(\left(2\sqrt{6}-4\sqrt{3}+5\sqrt{2}\right)\cdot3\sqrt{6}\)

\(=2\sqrt{6}\cdot3\sqrt{6}-4\sqrt{3}\cdot3\sqrt{6}+5\sqrt{2}\cdot3\sqrt{6}\)

\(=36-36\sqrt{2}+30\sqrt{3}\)

There is a lot of được dùng khi đứng sau nó là danh từ không đếm được

There are a lot of được dùng khi đứng sau nó là danh từ đếm được số nhiều

=> "There is a lot of" được dùng khi đứng sau nó là danh từ ko 
đếm được. 

"There are a lot of" được dùng khi đứng sau nó là DT đếm đc 
ở dạng số nhiều 

--
 

a)  A=x^2+4x+4=(x+2)^2.

Giờ ta tính giá trị của đa thức A với x=98:

A=(98+2)^2=100^2=10000

b)  B=x^3+9x^2+27x+27=(x+3)^3.

Thế x=-103 => (-103+3)^3=-1000000

c) Tách C = a⋅b−a⋅c+2⋅c−2⋅b rồi kết hợp lại thành C=(a−2)⋅b+(2−a)⋅c.

Thế a,b,c vào được vậy 

C=(2−2)⋅1.007+(2−2)⋅(−0.006) =0

d) Bài này khó quá mà tui nghĩ là đưa mấy cặp (2023^2-2022^2) thành dạng a^2-b^2=(a-b)(a+b) á

d: D=(2023^2-2022^2)+(2021^2-2020^2)+...+(3^2-2^2)+(1^2-0^2)

=2023+2022+...+3+2+1+0

=2023*2024/2=2047276

`|2x+1|-3=x+4`

`<=>|2x+1|=x+4+3=x+7(x>=-7)`

`**2x+1=x+7`

`<=>x=7-1=6(tm)`

`**2x+1=-x-7`

`<=>3x=-6`

`<=>x=-2(tm)`

`|3x-5|=1-3x(x<=1/3)`

`**3x-5=1-3x`

`<=>6x=6`

`<=>x=1(l)`

`**3x-5=3x-1`

`<=>-5=-1` vô lý

`|2x+2|+|x-1|=10`

Nếu `x>=1`

`pt<=>2x+2+x-1=10`

`<=>3x+1=10`

`<=>3x=9`

`<=>x=3(tm)`

Nếu `x<=-1`

`pt<=>-2x-2+1-x=10`

`<=>-1-3x=10`

`<=>-11=3x`

`<=>x=-11/3(tm)`

Nếu `-1<=x<=1`

`pt<=>2x+2+1-x=10`

`<=>x+3=10`

`<=>x=7(l)`

Vậy `S={3,-11/3}`

d) 

+) Với \(x< -4\), PT \(\Rightarrow3-x-x-4-2x-6=10\) \(\Leftrightarrow x=-\dfrac{17}{4}\)  (Nhận)

+) Với \(-4\le x\le-3\), PT \(\Rightarrow3-x+x+4-2x-6=10\) \(\Leftrightarrow x=-\dfrac{9}{2}\) (Loại)

+) Với \(-3< x\le3\), PT \(\Rightarrow3-x+x+4+2x+6=10\) \(\Leftrightarrow x=-\dfrac{3}{2}\) (Nhận)

+) Với \(x>3\), PT \(\Rightarrow x+3+x+4+2x+6=10\) \(\Leftrightarrow x=-\dfrac{3}{4}\) (Loại)

  Vậy \(x\in\left\{-\dfrac{3}{2};-\dfrac{17}{4}\right\}\) 

\(a,x=\dfrac{13}{2}-2\\ x=\dfrac{9}{2}\\ b,x=\dfrac{4}{5}\times\dfrac{3}{4}\\ x=\dfrac{12}{20}=\dfrac{3}{5}\)

=>8(x+1/x)^2+4[(x+1/x)^2-2]^2-4[(x+1/x)^2-2](x+1/x)^2=(x+4)^2

Đặt x+1/x=a(a>=2)

=>8a^2+4[a^2-2]^2-4[a^2-2]*a^2=(x+4)^2

=>8a^2+4a^4-16a^2+16-4a^4+8a^2=(x+4)^2

=>(x+4)^2=16

=>x+4=4 hoặc x+4=-4

=>x=-8;x=0

Điều kiện: \(x\ne0\)

\(\Leftrightarrow8\left(x+\dfrac{1}{x}\right)^2+4\left(x^2+\dfrac{1}{x^2}\right)\left[\left(x^2+\dfrac{1}{x^2}\right)-\left(x+\dfrac{1}{x}\right)^2\right]=\left(x+4\right)^2\)

\(\Leftrightarrow8\left(x+\dfrac{1}{x}\right)^2-8\left(x^2+\dfrac{1}{x^2}\right)=\left(x+4\right)^2\\ \Leftrightarrow\left(x+4\right)^2=16\\ \Rightarrow\left\{{}\begin{matrix}x=0\\x=-8\end{matrix}\right.\)

Vì \(x\ne0\) nên \(S=\left\{-8\right\}\)

Bạn nên dùng công thức trực quan cho bài toán như thế này nhé.

A. x = 2

B. \(\dfrac{3}{8}=\dfrac{6}{x}\)\(\Leftrightarrow x=\dfrac{6.8}{3}=16\)

C. x = 3

D. \(x=\dfrac{4.6}{8}=3\)

E. \(x=\dfrac{7}{3}\)

G.\(\dfrac{14}{13}=\dfrac{28}{10-x}\)

<=>\(14\left(10-x\right)=364\)

<=> 10 - x = 26 

<=> x = -16 

H. \(3\left(x+2\right)=4\left(x-5\right)\)

<=> 3x + 6  = 4x - 20 

<=> -x = -26

<=> x = 26

K. \(\dfrac{x}{2}=\dfrac{8}{x}\)

<=> \(x^2=16\)

<=> \(\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)

M. \(\left(x-2\right)^2=100\)

<=> \(\left[{}\begin{matrix}x-2=10\\x-2=-10\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=12\\x=-8\end{matrix}\right.\)

a=2

b=16

c=3

d=3

mik chỉ biết thế này thôi(ko chắc đúng=3)

A, \(\dfrac{x}{5}=\dfrac{2}{5}\Rightarrow x=2\)

B,\(\dfrac{3}{8}=\dfrac{6}{x};\dfrac{3}{8}=\dfrac{3\cdot2}{8\cdot2}=\dfrac{6}{16}\Rightarrow x=16\)

C,\(\dfrac{1}{9}=\dfrac{x}{27};\dfrac{1}{9}=\dfrac{1\cdot3}{9\cdot3}=\dfrac{3}{27}\Rightarrow x=3\)

D,\(\dfrac{4}{x}=\dfrac{8}{6};\dfrac{4}{x}=\dfrac{4\cdot2}{x\cdot2}=\dfrac{8}{2x}\)

   \(\Rightarrow2x=6;6=x:2;x=3\)

a.

\(\left(x^2-x+1\right)\left(x^2-x+2\right)=12\)

Đặt \(x^2-x+1=y\) ta được:

\(y\left(y+1\right)=12\)

\(\Leftrightarrow y^2+y-12=0\)

\(\Leftrightarrow y^2+4y-3y-12=0\)

\(\Leftrightarrow\left(y-3\right)\left(y+4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}y=3\\y=-4\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2-x+1=3\\x^2-x+1=-4\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2-x-2=0\\x^2-x+5=0\left(vn\right)\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)

b.

\(3y^3-7y^2-7y+3=0\)

\(\Leftrightarrow3\left(y^3+1\right)-7y\left(y+1\right)=0\)

\(\Leftrightarrow3\left(y+1\right)\left(y^2-y+1\right)-7y\left(y+1\right)=0\)

\(\Leftrightarrow\left(y+1\right)\left(3y^2-3y+3-7y\right)=0\)

\(\Leftrightarrow\left(y+1\right)\left(3y^2-10y+3\right)=0\)

\(\Leftrightarrow\left(y+1\right)\left(3y-1\right)\left(y-3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}y=-1\\y=\dfrac{1}{3}\\y=3\end{matrix}\right.\)

c.

\(x^2+2y^2=4x+4y-6=0\)

\(\Leftrightarrow x^2-4x+4+2y^2-4y+2=0\)

\(\Leftrightarrow\left(x-2\right)^2+2\left(y-1\right)^2=0\)

Do \(\left\{{}\begin{matrix}\left(x-2\right)^2\ge0\\\left(y-1\right)^2\ge0\end{matrix}\right.\) với mọi x;y

\(\Rightarrow\left(x-2\right)^2+2\left(y-1\right)^2\ge0\) ; \(\forall x;y\)

Dấu "=" xảy ra khi và chỉ khi:

\(\left\{{}\begin{matrix}x-2=0\\y-1=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)