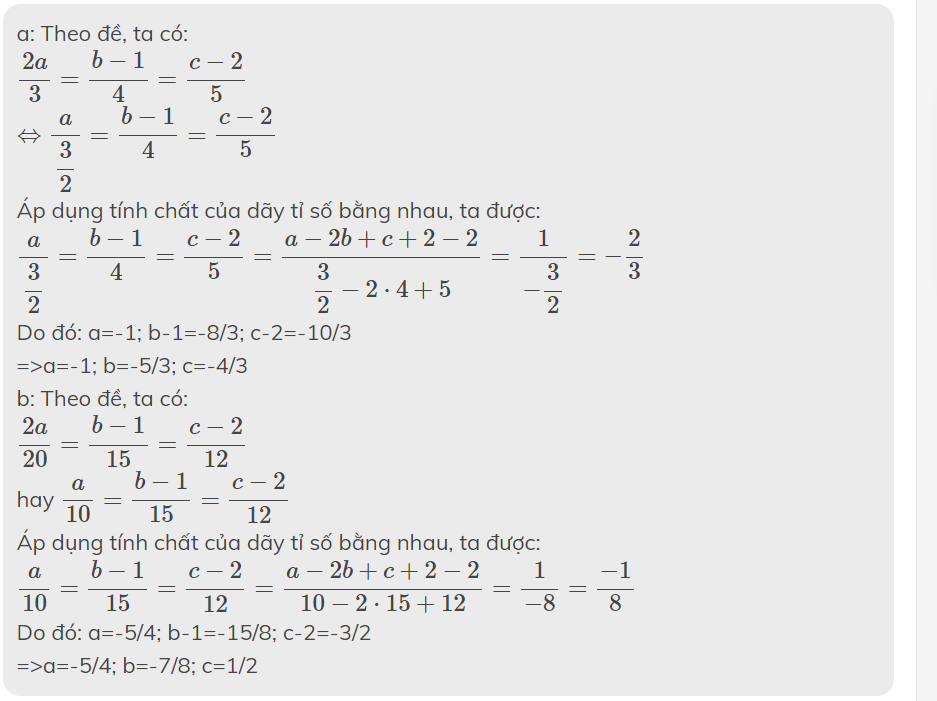Biết a+b=-1 và a^2 + b^2 = 5 Tính M= a^3 + b^3

Những câu hỏi liên quan
Biết a+b=-1 và a^2 + b^2 = 5 Tính M= a^3 + b^3
Chứng minh
a) ( a - b )^2 = ( a + b ) - 4ab. Tính ( a - b )^2009 biết a + b = -3 và ab = 4
b) a^3 + b^3 = ( a + b )^3 - 3ab(a + b ). Tính a^3 + b^3 = biết ab = 5 và a + b = -8
c) a^3 - b^3 = ( a - b )^3 + 3ab( a -b ). Tính a^3 - b^3 biết ab = -4 và a - b = 6
d) x^2 - 2xy + y^2 + 1 > 0 với mọi x và y
e) Tính x + y biết x^3 + y^3 = 91 và x^2 - xy + y^2 = 13
Bài 1.a, Chodfrac{a}{3}dfrac{b}{4}dfrac{c}{5} và a+b+c24. Tính M a.b + b.c + cab, Chodfrac{a}{2}dfrac{b}{3} dfrac{c}{4}dfrac{d}{5} và a+b+c+d -42. Tính N a.b +c.dBài 2.a, Biếtdfrac{x}{2}dfrac{y}{3}dfrac{z}{4} và x+y+z 24. Tính A 3x + 2y - 6zb, Biếtdfrac{x}{5}dfrac{y}{6}dfrac{z}{7} và x-y+z 6sqrt{2}. Tính B xy - yz
Đọc tiếp
Bài 1.
a, Cho\(\dfrac{a}{3}\)=\(\dfrac{b}{4}\)=\(\dfrac{c}{5}\) và a+b+c=24. Tính M = a.b + b.c + ca
b, Cho\(\dfrac{a}{2}\)=\(\dfrac{b}{3}\)= \(\dfrac{c}{4}\)=\(\dfrac{d}{5}\) và a+b+c+d = -42. Tính N = a.b +c.d
Bài 2.
a, Biết\(\dfrac{x}{2}\)=\(\dfrac{y}{3}\)=\(\dfrac{z}{4}\) và x+y+z= 24. Tính A = 3x + 2y - 6z
b, Biết\(\dfrac{x}{5}\)=\(\dfrac{y}{6}\)=\(\dfrac{z}{7}\) và x-y+z = 6\(\sqrt{2}\). Tính B = xy - yz
2:
a: Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y+z}{2+3+4}=\dfrac{24}{9}=\dfrac{8}{3}\)
=>x=16/3; y=8; z=32/3
A=3x+2y-6z
=3*16/3+2*8-6*32/3
=16+16-64
=-32
b: Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x}{5}=\dfrac{y}{6}=\dfrac{z}{7}=\dfrac{x-y+z}{5-6+7}=\dfrac{6\sqrt{2}}{6}=\sqrt{2}\)
=>x=5căn 2; y=6căn 2; y=7căn 2
B=xy-yz
=y(x-z)
=6căn 2(5căn 2-7căn 2)
=-6căn 2*2căn 2
=-24
Đúng 2
Bình luận (0)
bài 1 a)áp dụng dãy tỉ số bằng nhau ta có:\(\dfrac{a+b+c}{3+4+5}\)=\(\dfrac{24}{12}\)=2
a=2.3=6 ; b=2.4=8 ;c=2.5=10
M=ab+bc+ac=6.8+8.10+6.10=48+80+60=188
"nhưng bài còn lại làm tương tự"
Đúng 0
Bình luận (0)
1.A=(2/3+3/4+4/5+................+99/100)*(1/2+2/3+..............+98/99);B=(1/2+2/3+..............+99/100)*(2/3+3//4+...................+98/99)
Tính A và B bằng cách thuận tiện nhất.
2.Cho a=2008/2009;b=2009/2008;c=1/2009;d=2007/2008
Tính a-b+c+d
3.Tìm STN m biết:
2016+m/m+2520+m/m+3024+m/m
a) Biết 2a, b - 1, c - 2 Tỉ Lệ với 3, 4, 5 và a - 2b + c. Tính a, b, c
b) Biết 2a, b - 1, c - 2 Tỉ Lệ Nghịch 3, 4, 5 và a - 2b + c. Tính a, b, c
Tính \(A^5+B^5\) biết A + B = 3 và AB = 2
Tính \(A^6+B^6\) biết A + B = 2 và AB = 1
\(A^2+B^2=\left(A+B\right)^2-2AB=5\)
\(A^3+B^3=\left(A+B\right)^3-3AB\left(A+B\right)=9\)
\(A^5+B^5=\left(A^2+B^2\right)\left(A^3+B^3\right)-\left(AB\right)^2\left(A+B\right)=5.9-2^2.3=...\)
B.
\(A^2+B^2=\left(A+B\right)^2-2AB=2\)
\(A^6+B^6=\left(A^2\right)^3+\left(B^2\right)^3=\left(A^2+B^2\right)^3-3\left(AB\right)^2\left(A^2+B^2\right)=2^3-3.1^2.2=...\)
Đúng 2
Bình luận (0)
Ta có: \(A^2+B^2=\left(A+B\right)^2-2AB=3^2-2.2=5\)
\(A^5+B^5=\left(A^3+B^3\right)\left(A^2+B^2\right)-A^2B^2\left(A+B\right)=\left(A+B\right)\left(A^2-AB+B^2\right)\left(A^2+B^2\right)-A^2B^2\left(A+B\right)=3\left(5-2\right).5-2^2.3=33\)
Đúng 1
Bình luận (0)
1. Tìm a , b biết : \(\dfrac{a}{3}=\dfrac{b}{5}\) và \(a+b=32\)
2. Biết độ dài 3 cạnh của một tam giác tỉ lệ với 5; 7; 9 và chu vi tam giác
bằng 630 m. Tính độ dài 3 cạnh của tam giác đó.
1. Áp dụng TCDTSBN:
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{a+b}{3+5}=\dfrac{32}{8}=4\)
\(\Rightarrow\left\{{}\begin{matrix}a=12\\b=20\end{matrix}\right.\)
Đúng 2
Bình luận (7)
1. Áp dụng t/c dtsbn ta có:
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{a+b}{3+5}=\dfrac{32}{8}=4\)
\(\dfrac{a}{3}=4\Rightarrow a=12\\ \dfrac{b}{5}=4\Rightarrow b=20\)
2. gọi độ dài 3 cạnh tam giác lần lượt là a,b,c
Ta có: \(\left\{{}\begin{matrix}\dfrac{a}{5}=\dfrac{b}{7}=\dfrac{c}{9}\\a+b+c=630\left(m\right)\end{matrix}\right.\)
Áp dụng t/c dtsbn ta có:
\(\dfrac{a}{5}=\dfrac{b}{7}=\dfrac{c}{9}=\dfrac{a+b+c}{5+7+9}=\dfrac{630}{21}=30\left(m\right)\)
\(\dfrac{a}{5}=30\Rightarrow a=150\left(m\right)\\ \dfrac{b}{7}=30\Rightarrow b=210\left(m\right)\\ \dfrac{c}{9}=30\Rightarrow c=270\left(m\right)\)
Đúng 1
Bình luận (1)
Bài 3: Rút gọn biểu thức: a) (a+1)^2-(a-1)^2-3(a+1)(a-1) b) (m^3-m+1)2+(m^2-3)^2-2(m^2-3)(m^3-m+1) Bài 4: Tìm x, biết: a) ( 5x +1)^2 – ( 5x +3)( 5x – 3) 3 b) (3x-5)(5-3x)+9(x+1)^230 c) (x+4)^2-(x+1)(x-1)16 Bài 5: So sánh hai số A và B: a) A(3+1)(3^2+1)(3^4+1)(3^8+1)(3^(16)+1) và B3^(32)-1 b) và A 2011.2013 và B2012^2 Bài 6: a) C/ m HĐT : (a+b+ c)^2 a^2 +b^2 + c^2 +2ab +2ac + 2bc b)Áp dụng: cho x^2 + y^2 + z^2 5. Tính giá trị biểu thức: A ( 2x + 2y – z)^2 + ( 2y + 2z – x)^2 + ( 2z+2x – 2y)^2...
Đọc tiếp
Bài 3: Rút gọn biểu thức: a) (a+1)^2-(a-1)^2-3(a+1)(a-1) b) (m^3-m+1)2+(m^2-3)^2-2(m^2-3)(m^3-m+1) Bài 4: Tìm x, biết: a) ( 5x +1)^2 – ( 5x +3)( 5x – 3) = 3 b) (3x-5)(5-3x)+9(x+1)^2=30 c) (x+4)^2-(x+1)(x-1)=16 Bài 5: So sánh hai số A và B: a) A=(3+1)(3^2+1)(3^4+1)(3^8+1)(3^(16)+1) và B=3^(32)-1 b) và A= 2011.2013 và B=2012^2 Bài 6: a) C/ m HĐT : (a+b+ c)^2 = a^2 +b^2 + c^2 +2ab +2ac + 2bc b)Áp dụng: cho x^2 + y^2 + z^2 = 5. Tính giá trị biểu thức: A = ( 2x + 2y – z)^2 + ( 2y + 2z – x)^2 + ( 2z+2x – 2y)^2 Bài 7: Cho 5x^2 + 5y^2 + 8xy - 2x + 2y +2 = 0 Tính giá trị biểu thức B = ( x + y ) ^2018 + ( x -2)^ 2019 + ( y +1)^2020
\(3,\\ a,=a^2+2a+1-a^2+2a-1-3a^2+3=-3a^2+4a+3\\ b,=\left(m^3-m+1-m^2+3\right)^2=\left(m^3-m^2-m+4\right)^2\\ 4,\\ a,\Leftrightarrow25x^2+10x+1-25x^2+9=3\\ \Leftrightarrow10x=-7\Leftrightarrow x=-\dfrac{7}{10}\\ b,\Leftrightarrow-9x^2+30x-25+9x^2+18x+9=30\\ \Leftrightarrow48x=46\Leftrightarrow x=\dfrac{23}{24}\\ c,\Leftrightarrow x^2+8x+16-x^2+1=16\\ \Leftrightarrow8x=-1\Leftrightarrow x=-\dfrac{1}{8}\)
Đúng 2
Bình luận (0)
cho biết a/2 -b=c:2/3 và a,b,c khác 0. tính giá trị biểu thức Q=2018 - (c/a - 1/3)^5 x . (a/2 - 2) ^5 . (3/2 + b/c )^5
Bạn cần viết đề bài bằng công thức toán để được hỗ trợ tốt hơn (biểu tượng $\sum$ bên trái khung soạn thảo)
Đúng 1
Bình luận (0)